
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства замкнутости класса автоматных языков
Теорема 3.1.1. Класс автоматных языков замкнут относительно итерации, конкатенации и объединения. Доказательство. Без ограничения общности можно предположить, что каждый из исходных языков задан конечным автоматом с одним начальным и одним заключительным состоянием. Тогда во всех трех случаях результирующий автомат получается из исходных путем добавления нескольких Пример 3.1.2. Пусть
где
Тогда язык L(M1)* распознается конечным автоматом
Пример 3.1.3. Пусть
где
Тогда язык
а язык
Пересечение и дополнение автоматных языков Теорема 3.2.1. Класс автоматных языков замкнут относительно дополнения и пересечения. Доказательство. Если язык L распознается полным детерминированным конечным автоматом Пересечение выражается через объединение и дополнение (закон де Моргана). Замечание 3.2.2. Автоматность пересечения двух автоматных языков можно легко доказать и без привлечения теоремы 2.7.1. Для этого достаточно построить по двум конечным автоматам с однобуквенными переходами
новый конечный автомат
где
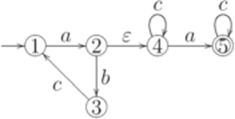
Лемма о разрастании для автоматных языков Лемма 3.3.1 (pumping lemma, лемма о разрастании, лемма о накачке, лемма-насос). Пусть L автоматный язык над алфавитом Доказательство. Пусть язык L распознается конечным автоматом
и Пример 3.3.2. Пусть
Положим p = 3. Тогда для любого слова
Примеры неавтоматных языков Пример 3.4.1. Рассмотрим язык Замечание 3.4.3. Условие, сформулированное в лемме 3.3.1, является необходимым для автоматности, но не достаточным. Пример 3.4.4. Пусть
Лемма 3.4.5*. Пусть L - автоматный язык над алфавитом Доказательство. Пусть L распознается конечным автоматом Эта лекция содержит дополнительные результаты, не используемые в дальнейшем изложении. В начале лекции доказывается замкнутость класса всех автоматных языков относительно взятия гомоморфного образа и относительно взятия полного гомоморфного прообраза. В разделе 4.2* определяются понятия побуквенного гомоморфизма и локального языка и доказывается еще один критерий автоматности: среди языков, не содержащих пустого слова, автоматными являются в точности образы локальных языков при побуквенных гомоморфизмах. В последнем разделе этой лекции устанавливается числовой критерий автоматности для языков над однобуквенным алфавитом (в терминах арифметических прогрессий) и доказывается связанное с длинами слов необходимое условие автоматности (для произвольного алфавита).
|
||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 143; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.220.114 (0.006 с.) |
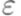 -переходов и состояний и назначения новых начальных и заключительных состояний.
-переходов и состояний и назначения новых начальных и заключительных состояний. . Рассмотрим конечный автомат
. Рассмотрим конечный автомат


 .
.
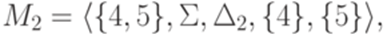

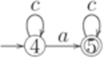
 распознается конечным автоматом
распознается конечным автоматом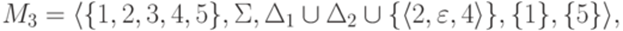
 распознается конечным автоматом
распознается конечным автоматом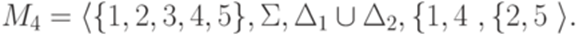

 , то язык
, то язык  распознается конечным автоматом
распознается конечным автоматом  .
.

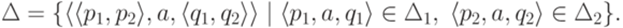
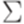 . Тогда найдется такое положительное целое число p, что для любого слова
. Тогда найдется такое положительное целое число p, что для любого слова  длины не меньше p можно подобрать слова
длины не меньше p можно подобрать слова  , для которых верно xyz = w,
, для которых верно xyz = w,  ,
,  и
и 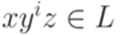 для всех
для всех 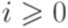 .
.
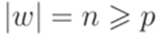 . Согласно принципу Дирихле найдутся такие индексы j и k, что
. Согласно принципу Дирихле найдутся такие индексы j и k, что 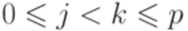 и qj = qk(ведь множество индексов
и qj = qk(ведь множество индексов  содержит p+1 натуральных чисел, а значения qi берутся из множества, содержащего всего p элементов). Выберем слова x, y и z так, что |x| = j, |y| = k - j и xyz = w.
содержит p+1 натуральных чисел, а значения qi берутся из множества, содержащего всего p элементов). Выберем слова x, y и z так, что |x| = j, |y| = k - j и xyz = w.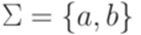 . Рассмотрим автоматный язык
. Рассмотрим автоматный язык
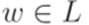 длины не меньше p найдутся слова
длины не меньше p найдутся слова 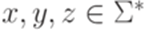 , соответствующие утверждению леммы 3.3.1. Действительно, если w = abu для некоторого слова u, то положим
, соответствующие утверждению леммы 3.3.1. Действительно, если w = abu для некоторого слова u, то положим  , y = ab, z = u; иначе w = aabu и можно положить x = a, y = ab, z = u.
, y = ab, z = u; иначе w = aabu и можно положить x = a, y = ab, z = u.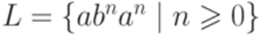 над алфавитом
над алфавитом 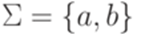 . Утверждение леммы 3.3.1 не выполняется ни для какого натурального числа p. Действительно, если w = abpap, то x = abk, y = bm, z = bp-k-map для некоторых
. Утверждение леммы 3.3.1 не выполняется ни для какого натурального числа p. Действительно, если w = abpap, то x = abk, y = bm, z = bp-k-map для некоторых 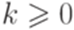 и
и 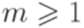 или
или  , y = abl, z = bp-lap для некоторого
, y = abl, z = bp-lap для некоторого 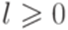 . В обоих случаях
. В обоих случаях 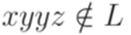 . Таким образом, язык L не является автоматным.
. Таким образом, язык L не является автоматным.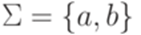 . Рассмотрим язык L = {akbman | k=0 или m=n}. Положим p = 1. Тогда для любого слова
. Рассмотрим язык L = {akbman | k=0 или m=n}. Положим p = 1. Тогда для любого слова 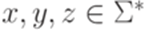 , соответствующие утверждению леммы 3.3.1. Тем не менее язык L не является автоматным, так как
, соответствующие утверждению леммы 3.3.1. Тем не менее язык L не является автоматным, так как
 и
и 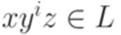 для всех
для всех  . Пусть
. Пусть 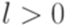 . Согласно принципу Дирихле найдутся такие натуральные числа j и k, что
. Согласно принципу Дирихле найдутся такие натуральные числа j и k, что 


