
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы решения задач нелинейного программирования
Методы прямого поиска. Суть этих методов состоит в том, что для поиска экстремального значения используются только значения ЦФ. Большинство методов этой группы основаны на экспериментальных данных и отражают опыт практических исследований, но строго теоретического обоснования не имеют. К достоинствам этих методов относится: · Простота алгоритма; · Возможность вычислить значение ЦФ практически во всех точках. Недостаток: · Трудность при обработке Седловых точек. К этим методам относятся: метод покоординатного спуска, метод Хука-Дживса, метод Розенброка, метод Пауэлла, метод регулярного многогранника, метод деформируемого многогранника, метод скользящего допуска. Метод покоординатного спуска Суть метода состоит в том, что поиск решения выполняется по каждой оси (направление изменения переменной xi). Выбирается первая переменная x1 (первая ось координат) и выполняется перемещение по этой оси. В каждой точке вычисляется значение ЦФ. Движение вдоль выбранной оси координат прекращается в тот момент, когда очередная точка будет иметь значение ЦФ большее, чем в предыдущей точке. Фиксируется лучшая достигнутая точка по текущей оси. Затем переходит ко второй оси координат (x2) и т.д., до последней переменной xn и затем процедура поиска повторяется, начиная с первой оси координат. Ели при проходе очередного цикла нельзя указать ни одного перемещения по любой оси координат, то уменьшают размер шага и выполняют ту же процедуру с меньшим шагом. Поиск экстремума прекращается, если размер шага становится меньше некоторой сколь угодно малой величины или, когда значение ЦФ в двух соседних точках становится практически одинаковой. Для организации поиска метода покоординатного спуска используется соотношение xk=xk-1+ak∙Uk, где xk – координаты текущей точки поиска, xk-1 – координаты предыдущей точки поиска, Uk – единичный вектор, определяющий направление спуска на k-м шаге. Может принимать значения +1 и -1, что обеспечивает перемещение по оси в одном из двух направлений. ak – размер шага. Одна итерация включает в себя проход по каждой оси координат. Алгоритм метода: 1. Определить координаты стартовой точки; 2. Вычислить значение ЦФ в этой точке; 3. Выбрать очередную ось и прибавить дельта x(шаг итерации)
4. Вычислить значение ЦФ в текущей точке; 5. Если значение ЦФ в текущей точке меньше, чем в предыдущей, то сделать еще один шаг в том же направлении и перейти к пункту 4. Если значение ЦФ в текущей точке больше, чем в предыдущей, то прейти к пункту 6. 6. Определить, был ли сделанный шаг в этом направлении первым, если да, то запомнить, что по текущей оси по текущему направлению сделан первый неудачный шаг. Перейти к пункту 7. Если нет, перейти к пункту 8. 7. Сменить направление движения по текущей оси и прейти к пункту 4. 8. Проверить все ли оси координат просмотрены, если да – перейти к пункту 9, если нет – перейти к пункту 3. 9. Проверить по всем ли осям координат сделано два неудачных первых шага. Если да, то уменьшить дельта x и перейти к пункту 10, если нет – перейти к пункту 3. 10. Проверить, достигнута ли требуемая точность, если да – перейти к шагу 11, если нет, то перейти к шагу 3 и начать просмотр с первой оси координат. 11. Остановить вычисления, вывести значение ЦФ и координаты точки экстремума.
Градиентные методы поиска экстремума при своей работе требуют вычисления не только значения ЦФ на каком-либо множестве точек, но и вычисления первой производной на том же множестве, иногда вычисление второй производной. Эти методы различаются разработанным математическим аппаратом и высоким быстродействием. К недостаткам относится невысокая точность результата и достаточно трудоемкие вычисления. Метод градиентного спуска. Суть его заключается в том, что в каждой i -той точке алгоритма вычисляется градиент. Определяются направления движения и шаг. Строится последовательность точек, переходя от одной точке к другой, достигается точка минимума. В точке минимума все элементы градиента принимают значение 0. Для определения координат очередной точки используется антиградиент – противоположное направление градиента. Размер шага модно определить по различным правилам: размер шага может быть с фиксированным коэффициентом изменения и с оптимальным подбором. Для случая с фиксированным коэффициентом изменение размера шага координаты точки на k-ом шаге по формуле: xk=x k-1-sk
Размер шага sk определяется по формуле sk=dkградf(xk-1) где dk – коэффициент изменения шага, dk<1 Критерий остановки алгоритма – это выполнение следующего условия |-градf(sk)|<E, E-точность вычисления.
Класс задач нелинейного программирования значительно шире класса задач линейного программирования, поэтому в практике экономико-математического моделирования необходимо знать и применять методы нелинейного программирования. Основные результаты в нелинейном программировании получены при рассмотрении задач, в которых система ограничений линейная, а целевая функция нелинейная. Даже в таких задачах оптимальное решение может быть найдено только для узкого класса целевых функций. В евклидовом пространстве Если определена область допустимых решений, то нахождение решение задачи нелинейного программирования сводится к определению такой точки этой области, через которую проходит гиперповерхность наивысшего (наинизшего) уровня Процесс нахождения решения задачи нелинейного программирования с использованием ее геометрической интерпретации включает следующие этапы: 1. Находят область допустимых решений задачи, определяемых соотношениями 2. Строят гиперповерхность 3. Определяют гиперповерхность наивысшего (наинизшего) уровня или устанавливают неразрешимость задачи из-за неограниченности функции 4. Находят точку области допустимых решений, через которую проходит гиперповерхность наивысшего (наинизшего) уровня, и определяют в ней значение функции Например, найти максимальное значение функции
Так как целевая функция нелинейная, то это задача нелинейного программирования. Областью допустимых решений данной задачи является многоугольник Построим линию уровня
Решив эту систему, получаем: Итак,
Как видим, в задаче нелинейного программирования точка максимального значения целевой функции не является в данном случае вершиной многоугольника решений.
Рассмотрим частный случай общей задачи нелинейного программирования, предполагая, что система ограничений содержит только уравнения, отсутствуют условия отрицательности переменных и
Такую задачу называют задачей на условный экстремум или классической задачей оптимизации. Чтобы найти решение этой задачи, введем набор переменных
находим частные производные
с m + n неизвестными Всякое решение системы уравнений определяет точку Таким образом, определение экстремальных точек задачи нелинейного программирования методом множителей Лагранжа включает следующие этапы: 1. Составляют функцию Лагранжа. 2. Находят частные производные от функции Лагранжа по переменным 3. Решая систему уравнений, находят точки, в которых целевая функция может иметь экстремум. 4. Среди точек, подозрительных на экстремум, находят точки, в которых достигается экстремум, и вычисляют значения целевой функции в этих точках.
Пример. Предприятию необходимо изготовить 180 деталей. Эти изделия могут быть изготовлены двумя технологическими способами. При производстве
Решение. Математическая модель задачи нелинейного программирования состоит в следующем: найти минимум функции Решим задачу, используя метод множителей Лагранжа. Найдем минимальное значение функции при условии
Вычислим её частные производные по
Перенесем в правые части первых двух уравнений
Решаем совместно систему, т.е. получаем координаты точки, удовлетворяющие условиям неотрицательности. Эта точка является подозрительной на экстремум. Используя вторые частные производные, выясняем, что в этой точке функция
Метод множителей Лагранжа можно применять и в том случае, когда условия связи представляют собой неравенства. Так, если требуется найти экстремум функции
Tочки, найденные в результате решения этой системы, вместе с точками, определёнными на первом этапе и удовлетворяющими условию Функцию Лагранжа можно трактовать и в определённом экономическом смысле. Если максимизируемую функцию интерпретировать как прибыль, а правые части неравенств
|
||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 208; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.196.217 (0.029 с.) |
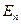 система ограничений определяет область допустимых решений задачи. В отличие от задач линейного программирования она не всегда является выпуклой областью.
система ограничений определяет область допустимых решений задачи. В отличие от задач линейного программирования она не всегда является выпуклой областью.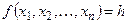 . Указанная точка может находиться как на границе области допустимых решений, так и внутри ее, в отличие от задач линейного программирования.
. Указанная точка может находиться как на границе области допустимых решений, так и внутри ее, в отличие от задач линейного программирования. (если она пуста, то задача не имеет решения).
(если она пуста, то задача не имеет решения).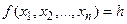 .
.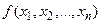 сверху (снизу) на множестве допустимых решений.
сверху (снизу) на множестве допустимых решений.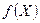 .
.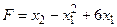 при условиях
при условиях
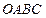 . Следовательно, для нахождения ее решения нужно определить такую точку многоугольника
. Следовательно, для нахождения ее решения нужно определить такую точку многоугольника  принимает максимальное значение.
принимает максимальное значение.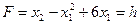 , где
, где  – некоторая постоянная, и исследуем ее поведение при различных значениях
– некоторая постоянная, и исследуем ее поведение при различных значениях 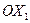 ,чем больше значение
,чем больше значение  , в которой гиперповерхность
, в которой гиперповерхность  касается стороны
касается стороны 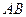 многоугольника
многоугольника 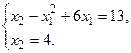

 при
при 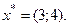

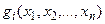 - функции, непрерывные вместе со своими частными производными (по крайней мере, вторая частная производная должна быть непрерывной).
- функции, непрерывные вместе со своими частными производными (по крайней мере, вторая частная производная должна быть непрерывной).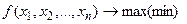
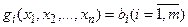
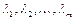 , называемых множителями Лагранжа, составим функцию Лагранжа
, называемых множителями Лагранжа, составим функцию Лагранжа ,
,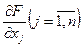 и
и 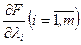 и рассматриваем систему
и рассматриваем систему  уравнений (здесь привлечём необходимое условие экстремума, заключающееся в том, что первая производная должна быть равна
уравнений (здесь привлечём необходимое условие экстремума, заключающееся в том, что первая производная должна быть равна 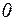 ):
):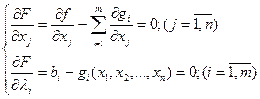
 .
.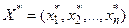 , в которой может иметь место экстремум функции
, в которой может иметь место экстремум функции 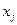 и
и  приравнивают их к нулю.
приравнивают их к нулю.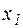 изделий I способом затраты равны
изделий I способом затраты равны  (руб.), а при изготовлении
(руб.), а при изготовлении 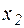 изделий II способом они составляют
изделий II способом они составляют 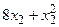 (руб.). Определить, сколько изделий каждым из способов следует изготовить так, чтобы общие затраты на производство продукции были минимальными.
(руб.). Определить, сколько изделий каждым из способов следует изготовить так, чтобы общие затраты на производство продукции были минимальными. при условиях
при условиях 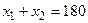 и
и  .
. , т.е. без учета требования неотрицательности переменных. Для этого составим функцию Лагранжа
, т.е. без учета требования неотрицательности переменных. Для этого составим функцию Лагранжа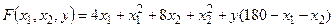 .
. ,
, 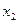 ,
,  и приравняем их к нулю:
и приравняем их к нулю:
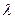 и, приравнивая их левые части, получим
и, приравнивая их левые части, получим 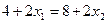 или
или 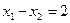 .
.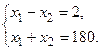
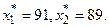
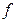 имеет условный минимум. То же получим, если исследование на условный экстремум функции
имеет условный минимум. То же получим, если исследование на условный экстремум функции  , полученной из
, полученной из  и подставим в целевую функцию, получим функцию одной переменной
и подставим в целевую функцию, получим функцию одной переменной 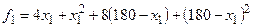 .
.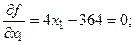 ;
; 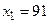 ;
; 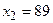 ;
;  , т.е. в этой точке имеем минимум.
, т.е. в этой точке имеем минимум.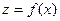 при условии
при условии  , то сначала следует найти точки безусловного экстремума функции
, то сначала следует найти точки безусловного экстремума функции 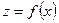 из уравнений
из уравнений 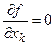 ;
;  , затем среди этих точек отобрать те, координаты которые удовлетворяют условию связи
, затем среди этих точек отобрать те, координаты которые удовлетворяют условию связи  , и, наконец, определить точки, удовлетворяющие системе уравнений:
, и, наконец, определить точки, удовлетворяющие системе уравнений: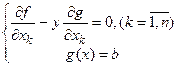 .
.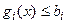 как величину отпущенных ресурсов, то множитель y можно рассматривать как стоимость единицы ресурсов. Тогда
как величину отпущенных ресурсов, то множитель y можно рассматривать как стоимость единицы ресурсов. Тогда  определит экономию ресурсов в денежном выражении, а функция Лагранжа
определит экономию ресурсов в денежном выражении, а функция Лагранжа 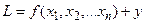
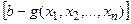 будет являться величиной общего дохода.
будет являться величиной общего дохода.


