
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
III. Матричный метод решенияСтр 1 из 2Следующая ⇒
ВЫСШАЯ МАТЕМАТИКА
Методическое пособие
Хабаровск Издательство ДВГУПС 2013 УДК [512.64 + 517.2 + 517.3] (075.8) ББК В 11я73 К 650
Рецензент – кандидат физико-математических наук, В.И. Жукова
Константинов, Н.С. П 650 Высшая математика: метод. пособие / Н.С. Константинов, М.С. Смотрова, Т.А. Богомякова,– Хабаровск: Изд-во ДВГУПС, 2012. – 49 с.: ил.
Методическое пособие разработано в соответствии с профессиональной образовательной программой. Представлены 4 контрольные работы, которые разбиты на три раздела, также содержатся методические указания по выполнению заданий. Предназначено для студентов 1-го курса ИИФО изучающих дисциплину «Высшая математика».
УДК [512.64 + 517.2 + 517.3] (075.8) ББК В 11я73
ВВЕДЕНИЕ Данное методическое пособие содержит четыре контрольные работы, рассчитанные на 2 семестра первого года обучения. В пособие включены методические указания по выполнению заданий. Весь материал, содержащийся в контрольных работах, разбит на три раздела. Такое разбиение выбрано для того, чтобы студент мог самостоятельно пополнить материал, выдаваемый преподавателем за короткое время, отведенное на аудиторные занятия. В конце каждого раздела находятся теоретические вопросы, которые даны студенту в помощь при подготовке к сдаче экзамена (зачета). Отвечая на вопросы устно, студент выстраивает последовательность ответа, что способствует повышению уровня самоорганизации. Содержащиеся в пособии практические задания требуется выполнить в тетради и сдать на проверку. В данном пособии теоретические вопросы и практические задания выступают как средства развития интеллектуальных способностей. Нумерация заданий в контрольных работах соответствует последней цифре шифра зачетной книжки студента. Примечание: если последняя цифра в шифре 0, то ей соответствует 10 вариант.
В пособие включен список литературы, которой студентам, по необходимости, рекомендуется пользоваться при выполнении заданий контрольных работ и для подготовки к сдаче экзамена. Материал в пособии выстроен таким образом, чтобы помочь студенту выйти на уровень самоорганизации, самообразования и самовоспитания при подготовке к экзамену (зачету).
Контрольная работа № 1 Раздел 1. Системы «n» линейных алгебраических уравнений с «n» неизвестными Система «n» линейных алгебраических уравнений с «n» неизвестными
совместна и имеет единственное решение, если определитель, составленный из коэффициентов Рассмотрим три метода решения систем алгебраических уравнений. I. Правило Крамера Решение системы (1) имеет вид
где II. Метод Гаусса При помощи элементарных преобразований [1] система уравнений (1) приводится к виду:
Из последнего уравнения непосредственно определяется неизвестная
Пример 1 Правило Крамера
Решение: вычислим
так как Находим дополнительные определители:
следовательно, и
Пример 2 Метод Гаусса Решение:
Следовательно, Пример 3 Запишем систему в виде
где
Решение:
Построим обратную матрицу Операция замены строк на столбцы называется транспонированием. Знак
т. е.
Примечания: 1. При умножении матрицы на число все элементы матрицы умножаются на это число. 2. Умножение матриц возможно, если число столбцов первого сомножителя равно числу строк второго сомножителя. 3. При умножении матриц элемент матрицы произведения равен сумме произведений элементов строки 1-го сомножителя матрицы на соответствующие элементы столбца 2-го сомножителя матрицы. Находим матрицу-решение:
Таким образом,
Теоретические вопросы к разделу 1 1. Определитель и его вычисление. 2. Алгебраическое дополнение и минор. 3. Определение матрицы, действия с матрицами. 4. Условие существования обратной матрицы. Единичная матрица.
Задание 1 к разделу 1 Решить систему алгебраических уравнений: 1) по правилу Крамера; 2) методом Гаусса; 3) матричным способом.
Примечание: здесь l, m, n – три последних цифры шифра студента. Например: Шифр КТ-98-Э-176, то l = 1, m = 7, n = 6. Раздел 2. Элементы векторной алгебры и аналитической геометрии Пусть заданы точки Вектором Модуль вектора Угол a между векторами
если векторы заданы координатами, то Пример 1 Найти скалярное произведение векторов Решение:
Площадь DABC вычисляется из определения геометрического смысла векторного произведения:
где
где Уравнение прямой, проходящей через точки А и В, имеет вид [1]:
Уравнение плоскости, проходящей через три точки, получаем из определения смешанного произведения [1], условия компланарности трех векторов:
Пример 2 Дано: A (2;1;3); B (2;0;5); C (5;-1;10). Найти: 1) периметр 2) угол 3) площадь 4) уравнение прямой (АВ); 5) уравнение плоскости (ABC). Решение: 1. Составим векторы
Найдём длины сторон, или модули векторов:
Тогда периметр равен Р = 2,236 + 7,874 + 5,916 = 16,026. 2. Угол Ð АСВ находится с помощью скалярного произведения:
т. е. 3. Площадь D АВС определяется с учётом геометрического смысла векторного произведения:
Векторное произведение
следовательно, и
4. Уравнение прямой (АВ):
или
Уравнение плоскости, проходящей через точки А, В и С:
следовательно, и общее уравнение плоскости имеет вид:
Теоретические вопросы к разделу 2 1. Вектор, его координаты, модуль. 2. Определение скалярного и векторного произведения. 3. Геометрический смысл модуля векторного и смешанного произведения.
4. Условия коллинеарности 2 векторов, уравнение прямой в пространстве. 5. Условие компланарности 3 векторов, уравнение плоскости. Задание 1 к разделу 2 Даны координаты точек А (0; 2; l); B (-1; 4; m); C (5; -1; n). Найти: 1) периметр 2) больший угол 3) площадь 4) уравнение прямой (АВ); 5) уравнение плоскости Примечание: l, m, n определяется также как и в задании 1 раздела 1.
Раздел 3. Базис. Разложение вектора по базисным векторам Базисом в пространстве Разложением вектора
где
Пример 1 Даны векторы Установить, что векторы Решение: Соотношение, записанное для вектора
т. е. получена алгебраическая система трёх уравнений с тремя неизвестными.
Решение системы удобнее вычислять методом Крамера:
следовательно, вектор
Теоретические вопросы к разделу 3 1. Какие векторы образуют базис на плоскости и в пространстве. 2. Разложение вектора по базисным векторам.
Задание 1 к разделу 3 Установить, что векторы Примечание: l, m, n определяется также как и в задании 1 раздела 1.
Контрольная работа № 2 Раздел 1. Комплексные числа Число вида Действия с комплексными числами: Сложение, вычитание и умножение выполняется по правилу действия с многочленами, с учетом, что 1. 2. Комплексное число
тогда
Для выполнения операции деления необходимо числитель и знаменатель умножить на комплексное число, сопряжённое знаменателю:
Расстояние от начала координат до точки
Непосредственно из рис. 1 следует, что
т. е. алгебраическая форма комплексного числа может быть переписана в тригонометрической форме:
Возведение в степень комплексного числа проводится по формуле Муавра, если Решим уравнение вида Правую часть уравнения приводим к тригонометрической форме
и из формулы Муавра получаем общее выражение для корня
где k = 0,1,...(n-1);
при k = 0 при k = 1 т. е. для каждого последующего корня аргумент получает приращение Пример 1 Выполнить действие Решение:
Пример 2 Решить уравнение:
Решение: Преобразуем правую часть:
теперь уравнение имеет вид
Находим общее выражение корня уравнения:
и все корни k = 0; k = 1; k = 2; Теоретические вопросы к разделу 1 1. Алгебраическая форма комплексного числа и действия с ними. 2. Тригонометрическая форма комплексного числа. Модуль и аргумент. 3. Возведение комплексного числа в целую положительную степень. 4. Извлечение корня из комплексного числа. Задание 1 к разделу 1 а) выполнить действия: б) найти корни уравнения: 1. а) 2. а) 3. а) 4. а) 5. а) 6. а) 7. а) 8. а) 9. а) 10. а) Раздел 2. Пределы Рассмотрим пределы четырех типов: I. Первый тип
где
где А – отношение коэффициентов при старших степенях в числителе и знаменателе.
Пример 1 Вычислить:
Наивысшая степень в числителе и знаменателе равна II. Второй тип
т.е.
В этом случае в числителе и знаменателе необходимо выделить множитель вида Примечание: формулы, требующиеся для вычисления пределов второго типа: 1) 2) 3) 4)
Пример 2 Вычислить:
Пример 3 Вычислить:
III. Третий тип Вычисление пределов этого типа основано на 1-ом замечательном пределе:
и понятии эквивалентных бесконечно малых величин, т. е. под знаком предела можно одну бесконечно малую величину заменить эквивалентной. Примеры эквивалентных бесконечно малых величин:
так как
Пример 4 Вычислить:
IV. Четвертый тип При вычислении этого предела используется 2-ой замечательный предел:
Для этого необходимо выполнить преобразование под знаком предела.
Пример 5 Вычислить:
Пример 6
где степень Теоретические вопросы к разделу 2 1. Определение первого замечательного предела. 2. Определение второго замечательного предела. 3. Определение эквивалентных бесконечно малых величин. 4. Применение эквивалентных бесконечно малых величин к вычислению пределов. Задание 1 к разделу 2 Найти пределы функций, не пользуясь правилом Лопиталя:
1.
2.
3.
4.
5.
6.
7.
8. 9.
10.
Раздел 3. Исследование непрерывности функции в заданных точках «
Функция
Пример 1 Дана функция Решение: Находим левосторонний и правосторонний пределы при
следовательно, и
Правосторонний предел:
следовательно, и
Таким образом, функция имеет разрыв в точке Рассмотрим эту функцию в окрестности
и равны значению функции в этой точке Схематический чертеж функции (рис. 3):
Рис. 3
Теоретические вопросы к разделу 3 1. Условия непрерывности функции в точке. Левосторонние и правосторонние пределы. 2. Классификация точек разрыва.
Задание 1 к разделу 3. Задана функция 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Задание 2 к разделу 3
Задана функция y = f (x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
Контрольная работа № 3 Раздел 1. Производные Таблица производных основных элементарных функций:
Правила дифференцирования:
где Правила действий со степенями: 1. 2. 3. 4.
Пример 1 Найти производную функции
Решение:
Пример 2 Найти производную функции
Решение: функция сложная, и её можно записать с помощью промежуточных аргументов:
Каждый из промежуточных аргументов является основной элементарной функцией (см. таблицу производных, стр. 25):
Пример 3 Найти производную произведения 2-х функций:
Решение:
где
Пример 4 Найти производную частного:
Решение:
Теоретические вопросы к разделу 1 1. Определение производной в точке, геометрический смысл. 2. Правила дифференцирования суммы, частного двух функций. 3. Правило дифференцирования сложной функции.
Задание 1 к разделу 1 Найти производные данных функций: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Раздел 2. Экстремум функции, его классификация Необходимое условие экстремума в точке При этом: · если · если · если производная свой знак не меняет, то экстремума нет; точка Пример 1 Исследовать на экстремум:
Решение:
Находим знак производной слева и справа от точки
т.е.
Пример 2 Исследовать на экстремум:
Решение:
Находим знак производной в окрестности критической точки:
Пример 3 Исследовать на экстремум:
Решение:
Находим знаки производной в окрестности критической точки
| Поделиться:
| |
 © ДВГУПС, 2013
© ДВГУПС, 2013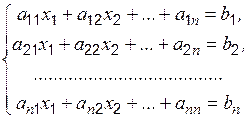 (1)
(1)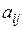 , отличен от нуля, т. е.
, отличен от нуля, т. е.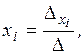
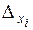 – дополнительный определитель, полученный из определителя
– дополнительный определитель, полученный из определителя 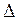 путём замены столбца коэффициентов при
путём замены столбца коэффициентов при 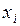 столбцом свободных членов, состоящим из
столбцом свободных членов, состоящим из 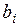 правой части уравнения.
правой части уравнения.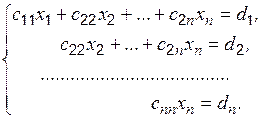
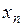 , затем ее значение подставляется в предпоследнее и находится
, затем ее значение подставляется в предпоследнее и находится 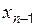 . Этот процесс необходимо повторять до первого уравнения включительно.
. Этот процесс необходимо повторять до первого уравнения включительно.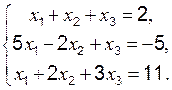
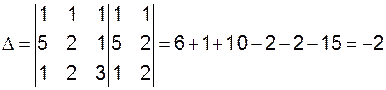 ,
,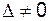 , то данная система совместна и имеет единственное решение.
, то данная система совместна и имеет единственное решение.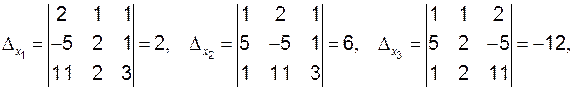
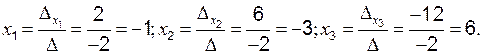
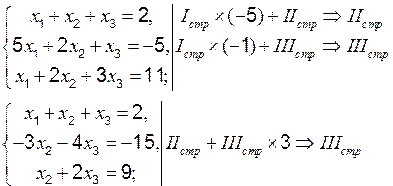
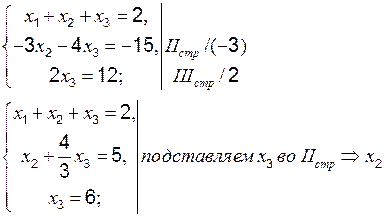
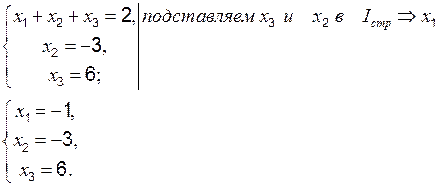
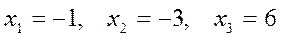 .
. ,
,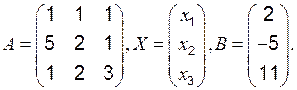
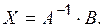
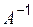 . Вычислим алгебраические дополнения ко всем элементам, причём алгебраические дополнения, вычисленные для элементов первой строки, записываются первым столбцом матрицы
. Вычислим алгебраические дополнения ко всем элементам, причём алгебраические дополнения, вычисленные для элементов первой строки, записываются первым столбцом матрицы 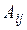 определяется как
определяется как 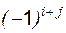 :
: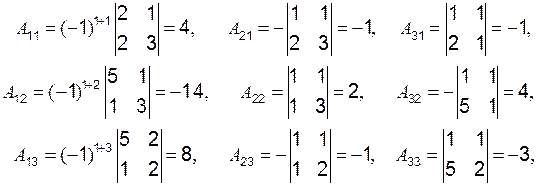
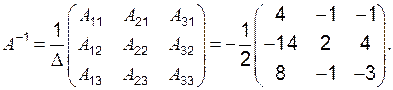
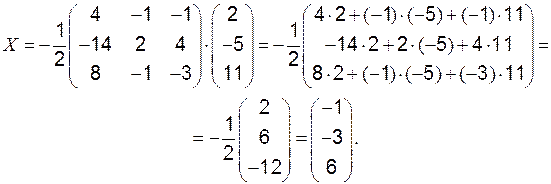
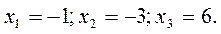
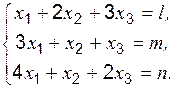
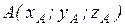 ;
; 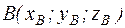 ;
; 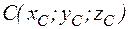 .
.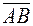 называется направленный отрезок с координатами
называется направленный отрезок с координатами 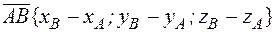 .
.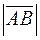 (расстояние между точками А и В) равен
(расстояние между точками А и В) равен  .
.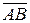 и
и 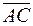 находится из определения скалярного произведения [2]:
находится из определения скалярного произведения [2]: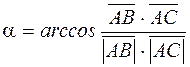 ,
,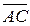 (скалярное произведение) равно сумме произведений соответствующих координат.
(скалярное произведение) равно сумме произведений соответствующих координат.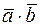 , если
, если 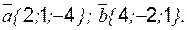
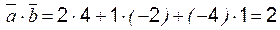 .
.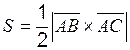 ,
,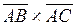 – векторное произведение, модуль которого равен:
– векторное произведение, модуль которого равен: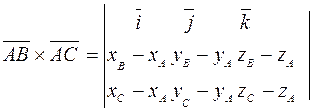 ,
, – ортонормированный базис системы координат X, Y, Z.
– ортонормированный базис системы координат X, Y, Z.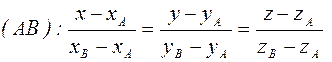 .
.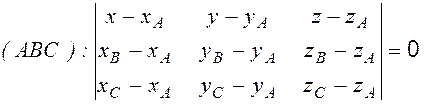 .
. ABC, с точностью до 0,01;
ABC, с точностью до 0,01;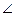 ВСА, с точностью до 0,1°;
ВСА, с точностью до 0,1°;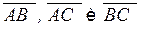
 .
.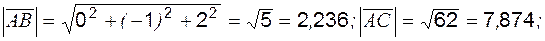
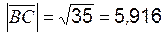 .
.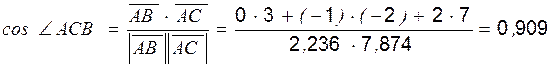 ,
,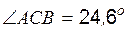 .
.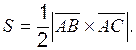
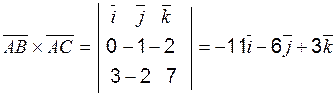 ,
,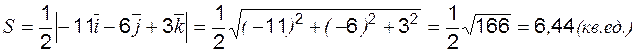 .
.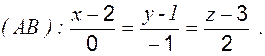
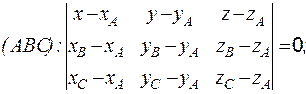
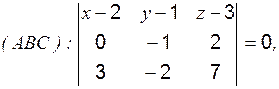
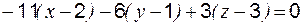 ;
;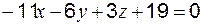 .
. называется совокупность «n» векторов, позволяющих представить любой вектор из этого пространства в виде разложения по данному базису. В
называется совокупность «n» векторов, позволяющих представить любой вектор из этого пространства в виде разложения по данному базису. В  базис образуют два любых неколлинеарных вектора, в
базис образуют два любых неколлинеарных вектора, в 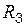 – три любых некомпланарных вектора. Из свойства смешанного произведения известно, что произведение трёх некомпланарных векторов отлично от нуля.
– три любых некомпланарных вектора. Из свойства смешанного произведения известно, что произведение трёх некомпланарных векторов отлично от нуля.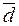 по базису
по базису 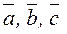 называется выражение
называется выражение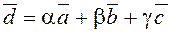 ,
,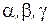 – коэффициенты разложения, или координаты вектора
– коэффициенты разложения, или координаты вектора 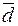 в базисе
в базисе 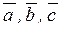 .
.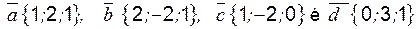 .
.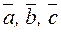 образуют базис, и найти координаты вектора
образуют базис, и найти координаты вектора 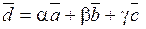 , справедливо для каждой из проекций
, справедливо для каждой из проекций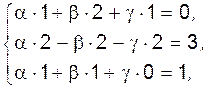
 ,
,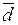 имеет разложение в базисе
имеет разложение в базисе 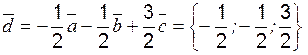 .
.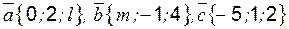 образуют базис, и найти координаты вектора
образуют базис, и найти координаты вектора 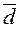 в этом базисе, если
в этом базисе, если 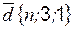 .
.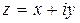 называется комплексным числом, где
называется комплексным числом, где 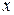 и
и 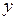 – действительные числа, а
– действительные числа, а 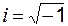 – называется мнимой единицей,
– называется мнимой единицей, 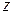 ,
, 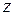 .
.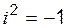 :
: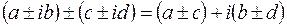 ;
;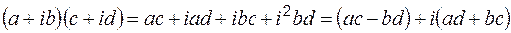 .
.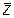 называют сопряжённым числу
называют сопряжённым числу 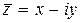 ,
, 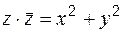 .
.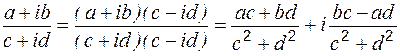 .
.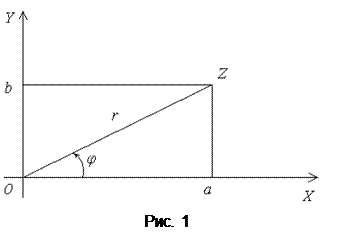 Рассмотрим тригонометрическую форму комплексного числа. Для этого ведём комплексную плоскость, на оси ОХ откладываем действительную часть комплексного числа, на OY – мнимую, тогда число
Рассмотрим тригонометрическую форму комплексного числа. Для этого ведём комплексную плоскость, на оси ОХ откладываем действительную часть комплексного числа, на OY – мнимую, тогда число  на плоскости обозначается буквой
на плоскости обозначается буквой  , угол
, угол  – аргумент комплексного числа (рис. 1).
– аргумент комплексного числа (рис. 1).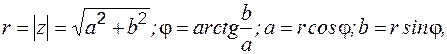
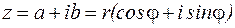 .
.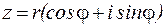 , то
, то 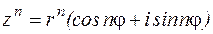 , т. е. при возведение в степень “ n ” модуль возводится в эту степень, а аргумент увеличивается в “ n ” раз.
, т. е. при возведение в степень “ n ” модуль возводится в эту степень, а аргумент увеличивается в “ n ” раз.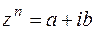 .
.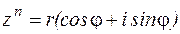 ,
,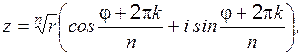
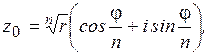
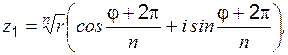 и т.д.
и т.д.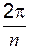 .
.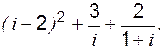
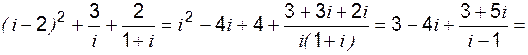
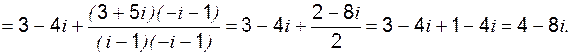
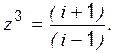
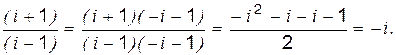
 Приведём число “- i ” к тригонометрической форме:
Приведём число “- i ” к тригонометрической форме: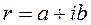 ; a =0; b =-1; r =1;
; a =0; b =-1; r =1; 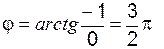 (рис. 2),
(рис. 2),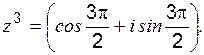
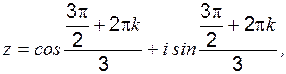
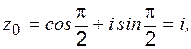
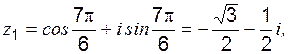
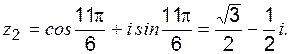
 б)
б) 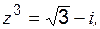
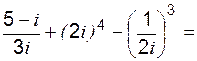 , б)
, б) 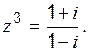
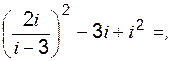 б)
б) 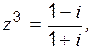
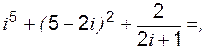 б)
б) 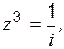
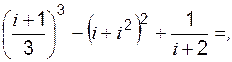 б)
б) 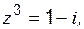
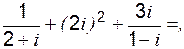 б)
б) 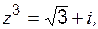
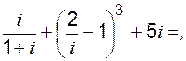 б)
б) 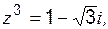
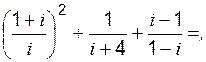 б)
б) 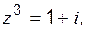
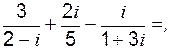 б)
б) 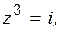
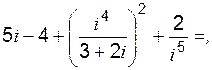 б)
б) 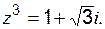
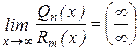 ,
,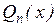 ,
, 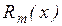 – многочлены с наивысшими степенями «
– многочлены с наивысшими степенями «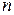 » и «
» и « », причем
», причем 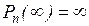 и
и 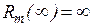 . Тогда
. Тогда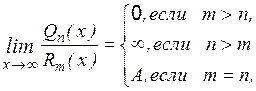 ,
,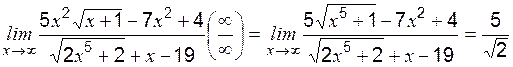 .
. , при этом коэффициент при старшей степени в числителе равен
, при этом коэффициент при старшей степени в числителе равен 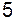 , а в знаменателе –
, а в знаменателе – 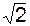 , поэтому предел равен отношению этих коэффициентов
, поэтому предел равен отношению этих коэффициентов 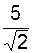 .
.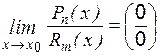 ,
,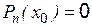 и
и 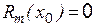 .
.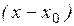 и сократить, чтобы устранить неопределенность вида
и сократить, чтобы устранить неопределенность вида  .
.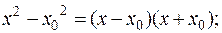
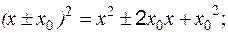
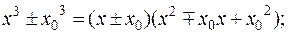
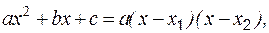 где
где 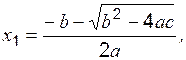
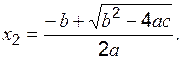
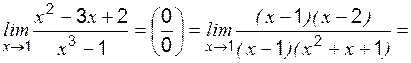
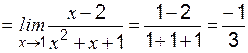 .
.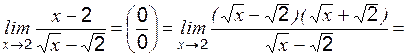
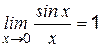 .
.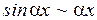 ,
, 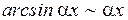 ,
, 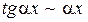 .
.  ,
,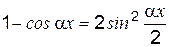 .
.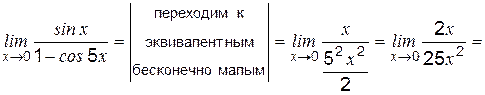
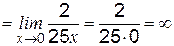 .
.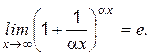
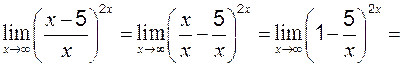
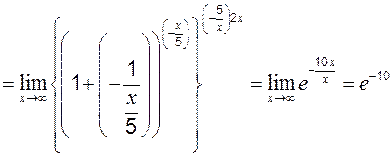 .
.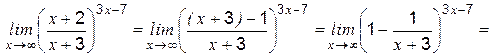
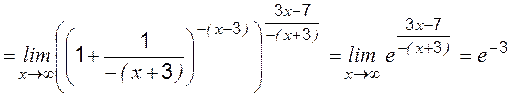 ,
,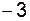 определяется следующим образом: наивысшие степени в числителе и знаменателе дроби равны
определяется следующим образом: наивысшие степени в числителе и знаменателе дроби равны 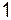 , при этом коэффициент при старшей степени в числителе равен
, при этом коэффициент при старшей степени в числителе равен 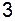 , а в знаменателе:
, а в знаменателе: 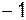 , поэтому предел равен отношению этих коэффициентов
, поэтому предел равен отношению этих коэффициентов 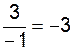 .
.
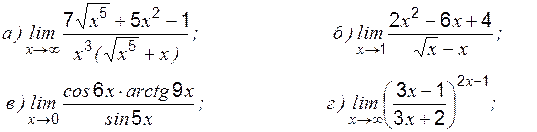
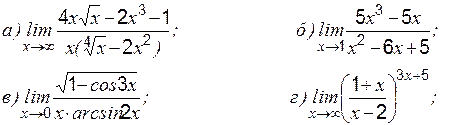
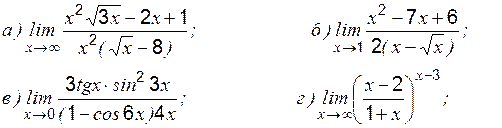
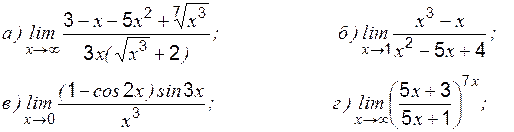
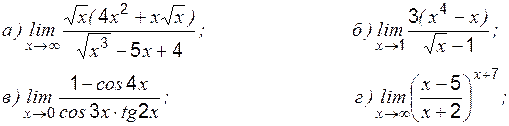
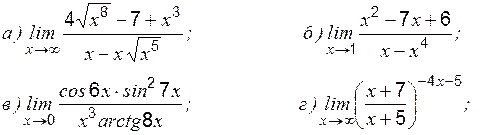
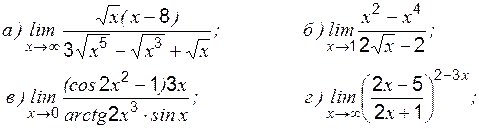
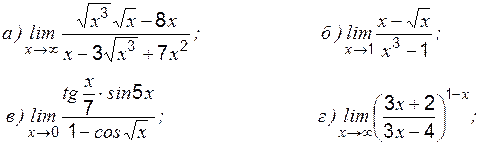
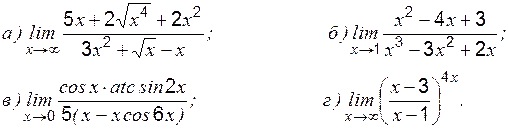
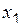 » и «
» и «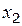 »
»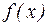 считается непрерывной в точке
считается непрерывной в точке 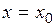 , если пределы слева и справа существуют и равны значению
, если пределы слева и справа существуют и равны значению 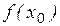 .
. , исследовать на непрерывность в точках
, исследовать на непрерывность в точках 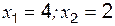 , сделать схематический чертеж.
, сделать схематический чертеж.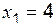 :
: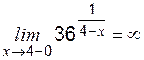 (левосторонний предел при
(левосторонний предел при 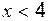 , поскольку
, поскольку 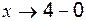 ), т. е. показатель степени
), т. е. показатель степени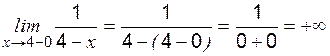 ,
,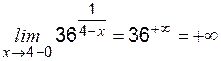 .
.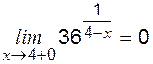 (правосторонний предел при
(правосторонний предел при 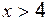 , поскольку
, поскольку  ), т. е. показатель степени
), т. е. показатель степени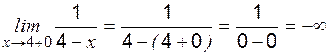 ,
,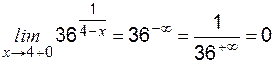 .
.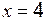 .
.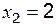 . В этом случае левосторонний и правосторонний пределы равны:
. В этом случае левосторонний и правосторонний пределы равны: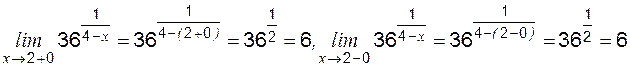
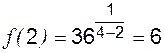 , следовательно, в точке
, следовательно, в точке 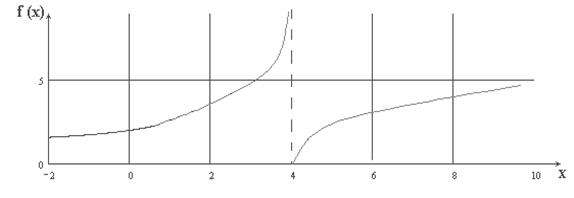
 и два значения аргумента
и два значения аргумента 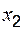 . Требуется установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента, и сделать схематический чертеж.
. Требуется установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента, и сделать схематический чертеж.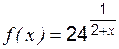 ,
,  ,
, 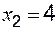 ;
;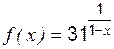 ,
, 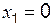 ,
, 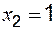 ;
;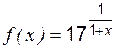 ,
, 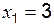 ,
, 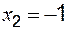 ;
;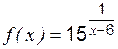 ,
, 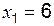 ,
, 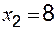 ;
;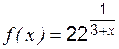 ,
, 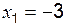 ,
, 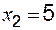 ;
;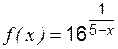 ,
, 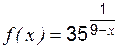 ,
, 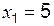 ,
, 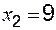 ;
;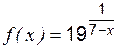 ,
, 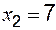 ;
;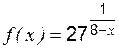 ,
, 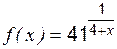 ,
, 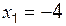 ,
, 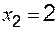 .
.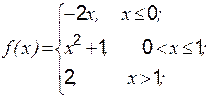
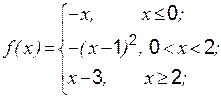
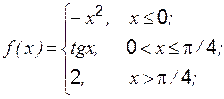
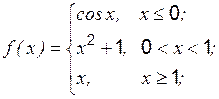
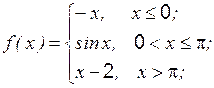
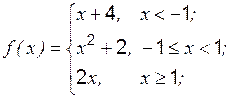
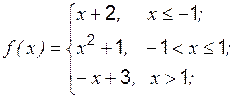
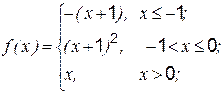
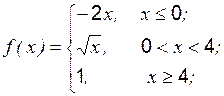
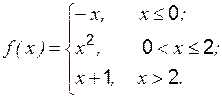
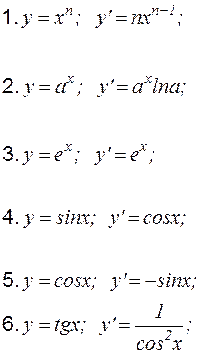
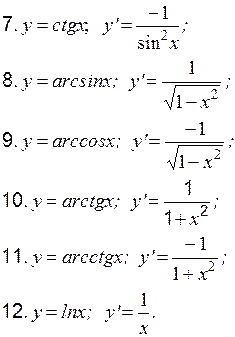
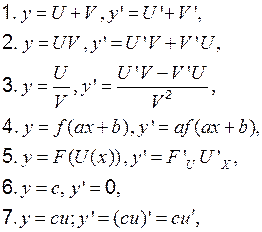
 некоторые постоянные.
некоторые постоянные.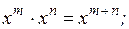
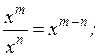
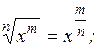
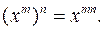
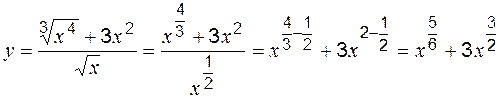 .
.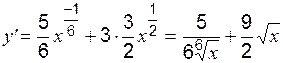 .
.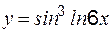 .
.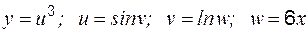 .
.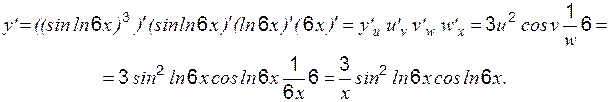
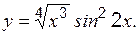
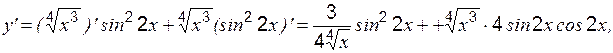
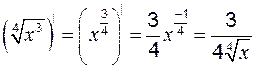 ;
;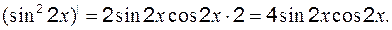
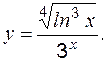
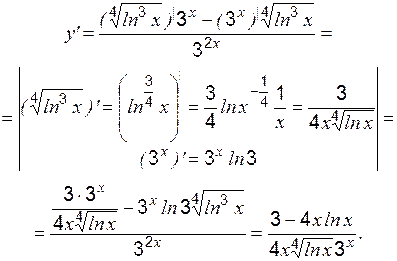
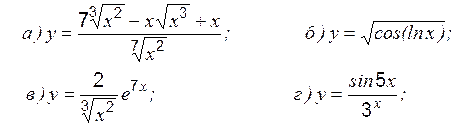
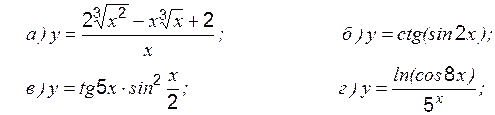
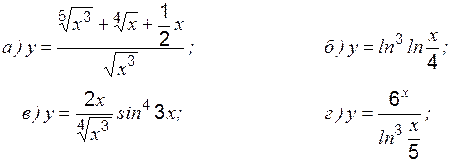
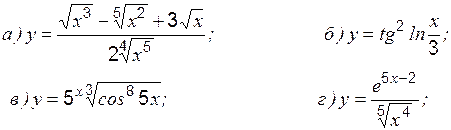
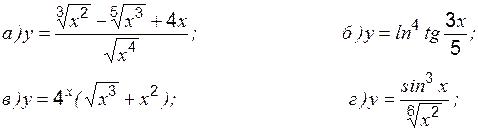
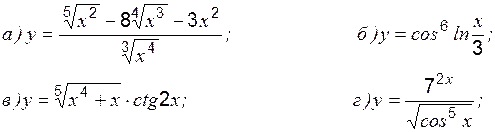

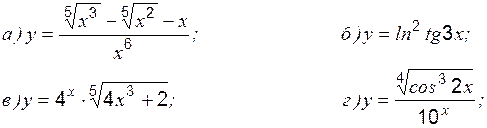
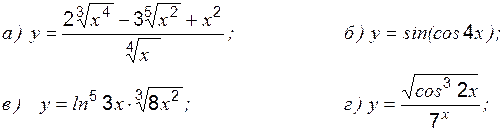
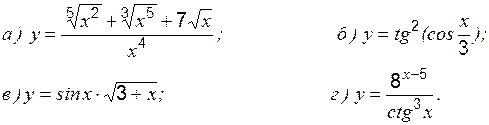
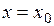 :
: 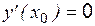 , или
, или 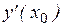 – не существует.
– не существует.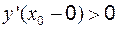 ;
; 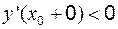 – в точке
– в точке 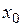 функция имеет максимум;
функция имеет максимум; 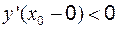 ;
; 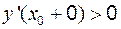 – минимум;
– минимум;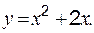
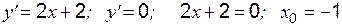 – критическая точка.
– критическая точка.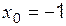 :
: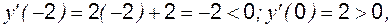
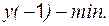
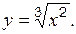
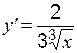 – не существует в точке
– не существует в точке 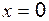 .
.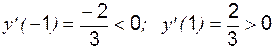 , т. е.
, т. е. 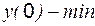 .
.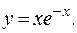
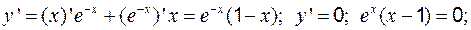
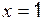 – критическая точка.
– критическая точка.


