Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о логической функции и логическом устройстве
Для обозначения различной информации – предметов, понятий, действий – мы пользуемся словами. Запись слов производится с помощью букв из некоторого их набора, называемого алфавитом. В цифровой технике для тех же целей пользуются кодовыми словами. Особенность этих слов заключается в том, что все они имеют чаще всего одинаковую длину (т.е. состоят из одного и того же количества букв), и для их построения используется простейший алфавит из двух букв. Эти буквы принято обозначать символами 0 и 1. Таким образом, кодовое слово в цифровой технике есть определенной длины последовательность символов 0 и 1, например 10111011. Такими кодовыми словами могут представляться и числа, в этом случае 0 и 1 совпадают по смыслу с обычными арабскими цифрами. При представлении кодовым словом некоторой нечисловой информации, чтобы отличать символы 0 и 1 от арабских цифр, будем эти символы называть логическим нулем и логической единицей (лог. 0 и лог. 1). Если длина кодовых слов составляет n разрядов, то можно построить 2n различных комбинаций – кодовых слов. Например, при n = 3 можно построить 23 = 8 слов: 000, 001, 010, 011, 100, 101, 110, 111. Информация, которая передается между отдельными блоками сложного цифрового устройства, передается в виде кодовых слов. Таким образом, на входы каждого блока поступают кодовые слова, на выходе блока образуется новое кодовое слово, представляющее собой результат обработки входных слов. Выходное слово зависит от того, какие слова поступают на входы узла. Поэтому можно говорить, что выходное слово есть функция, для которой аргументами являются входные слова. Для того чтобы подчеркнуть особенность таких функций, состоящую в том, что функция и ее аргументы могут принимать значения лог. 0 и лог. 1, будем эти функции называть функциями алгебры логики. Устройства, предназначенные для формирования функций алгебры логики, называются логическими устройствами или цифровыми устройствами. Логические (Булевы) функции Рассмотрим функции одной переменной y = f(x). Пронумеруем эти функции (их четыре) и расположим в виде таблицы:
Видно, что f0(х) = 0, a f3(х) = 1, т.е. эти две функции не зависят от х, f1(х) = х, т.е. она не меняет аргумента. Функция f2(х) действительно содержательная функция. Она принимает значения, противоположные значениям аргумента, обозначается
Рассмотрим функции двух переменных y = f(x1, x 2). Число этих функций равно 24 = 16. Пронумеруем и расположим их в естественном порядке.
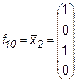
Рассмотрим более подробно эти функции. Две из них f0 = 0 и f15 = 1 являются константами. Функции
являются по существу функциями одной переменной. Наиболее важные функции двух переменных имеют специальные названия и обозначения. Заметим, что эти обозначения не всегда общеприняты. Перечислим семь важнейших функций. 1. Конъюнкция (функция И)
Конъюнкция (логическое умножение) переменных x1 и х2 равна лог. 1 в том случае, когда и x1 и х2 равны лог. 1 (отсюда и возникло название операции логическое И). Конъюнкция – это фактически обычное умножение (нулей и единиц). Иногда эту функцию обозначают x1 & x 2 или x1 2. Дизъюнкция (функция ИЛИ)
Дизъюнкци я (логическое сложение) переменных x1 и х2 равна лог. 1, если или x1 или х2 равна лог. 1 (отсюда название операции логическое ИЛИ). В тех случаях, когда число переменных больше двух, их конъюнкция равна лог. 1 при равенстве лог. 1 всех переменных; дизъюнкция равняется лог. 1, если хотя бы одна из переменных имеет значение лог. 1. 3. Импликация (следование)
Иногда импликацию обозначают x1 כ х2 или x1 → х2 (читается “из x1 следует х2 ”). Это очень важная функция, особенно в логике. Ее можно рассматривать следующим образом: если x1 = 0 (т. е. x1 “ложно”), то из этого факта можно вывести и “ложь”, и “истину” (и это будет правильно), если х2 = 1(т.е. х2 “истинно”), то истина выводится и из “лжи” и из “истины”, и это тоже правильно. Только вывод “из истины ложь” является неверным. Заметим, что любая теорема всегда фактически содержит эту логическую функцию. 4. Сложение по модулю 2, Исключающее ИЛИ (здесь и далее, если не оговорено противное, знаком “+” мы будем обозначать такое сложение):
5. Эквивалентность или подобие ~
Эта f9 = 1 тогда и только тогда, когда х1 = х2. 6. Штрих Шеффера
Иногда эту функцию называют “ НЕ И ” (так как она равна отрицанию конъюнкции). 7. Стрелка Пирса (иногда эту функцию называют штрих Лукасевича)
Эта функция является отрицанием дизъюнкции, и поэтому иногда ее называют “не ИЛИ”. Заметим, что свойства последних двух функций похожи между собой и, может быть, поэтому в литературе их часто путают (т. е. называют f8 штрихом Шеффера, а f14 – стрелкой Пирса). Три оставшиеся функции, (f2, f4 и f11) особого значения в дискретной математике не имеют. Операцию отрицания называют инверсией или дополнением. Для ее обозначения используют черту над соответствующим выражением. Операция определяется следующими постулатами: если х = 1, то В математике установлен определенный порядок выполнения операций в сложном выражении. Подобно этому в сложном логическом выражении вначале выполняются операции инверсии, затем операции конъюнкции и в последнюю очередь операции дизъюнкции. Теоремы булевой алгебры отражают связи, существующие между операциями, выполняемыми над логическими переменными. Сформулируем наиболее важные из них: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. Справедливость всех перечисленных теорем может быть до-казана непосредственной подстановкой.
1.1.3. Способы задания логических функций В классической математике для задания функции обычно используются два способа: аналитический (запись формулой) и табличный (таблицами значений функций). Для описания функций алгебры логики могут быть использованы различные способы. Основными из них являются описание функций в словесной форме, в виде таблиц истинности и алгебраических выражений. Проиллюстрируем словесное описание функции алгебры логики на примере. Логическая функция трех переменных равна 1, если хотя бы две входные переменные равны 1. Данный вид описания наиболее часто применяется для первоначального, исходного описания поведения логического устройства. Таблица, содержащая все возможные комбинации входных переменных xn-1 …x1x0 и соответствующие им значения выходных переменных y i, называется таблицей истинности или комбинационной таблицей. В общем случае таблица истинности содержит 2n строк и m+n столбцов, где n – количество входных сигналов, а m – выходных. При описании функций алгебры логики алгебраическим выражением используются две стандартные формы ее представления – так называемые дизъюнктивная и конъюнктивная нормальные формы. Дизъюнктивной нормальной формой (ДНФ) называется логическая сумма элементарных логических произведений, в каждое из которых аргумент или его инверсия входит один раз. ДНФ может быть получена из таблицы истинности с использованием следующего алгоритма: а) для каждого набора переменных, на котором функция алгебры логики равна единице, записывают элементарные логические произведения входных переменных, причем переменные, равные нулю, записывают с инверсией. Полученные произведения называют конституентами единицы;
б) логически суммируют все конституенты единицы. ДНФ, полученную суммированием конституент единицы, называют совершенной (СДНФ). Конъюнктивной нормальной формой (КНФ) называется логическое произведение элементарных логических сумм, в каждую из которых аргумент или его инверсия входят один раз. КНФ может быть получена из таблицы истинности с использованием следующего алгоритма: а) для каждого набора переменных, на котором функция алгебры логики равна нулю, записывают элементарные логические суммы входных переменных, причем переменные, значения которых равны единице, записывают с инверсией. Полученные суммы называют конституентами нуля; б) логически перемножают все полученные конституенты нуля. КНФ, полученную суммированием конституент нуля, также называют совершенной (СКНФ). Пример 1.1. Запишите дизъюнктивную и конъюнктивную нормальные формы для следующей таблицы истинности:
Решение. Согласно приведенному выше алгоритму дизъюнктивная нормальная форма примет вид
а конъюнктивная нормальная форма определится как
Иногда удобнее применять не саму функцию алгебры логики, а ее инверсию. В этом случае при использовании вышеописанных методик для записи СДНФ необходимо выбирать нулевые, а для записи СКНФ – единичные значения функции.
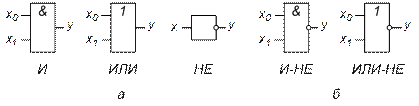
Логические элементы Функция алгебры логики однозначно определяет внутреннюю структуру логического устройства. С помощью элементарных узлов, реализующих основные логические операции, можно построить логическую схему, выполняющую заданный алгоритм преобразования исходных логических переменных. В соответствии с перечнем логических операций различают три основных логических элемента: И, ИЛИ, НЕ. Условные графические обозначения этих логических элементов показаны на рис. 1.1.
Рис. 1.1. Условные графические обозначения основных (а) и совмещающих в себе две функции (б) логических элементов Число входов логических элементов И или ИЛИ может быть произвольным. Элемент НЕ всегда имеет только один вход. Для построения логической схемы необходимо логические элементы, предназначенные для выполнения логических операций, указанных в функции алгебры логики, располагать от входа в порядке, определенном булевым выражением. Пример 1.2. Построить структурную схему логического устройства по функции алгебры логики (1.1).
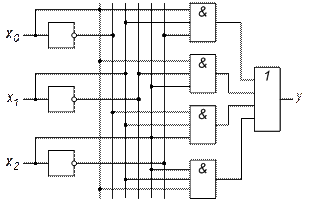
Решение приведено на рис. 1.2
Рис. 1.2. Пример структурной схемы логического устройства
Функционально полной системой называется совокупность логических элементов, позволяющая реализовать логическую схему произвольной сложности. На практике широкое применение нашли логические элементы, совмещающие в себе функции логического сложения и отрицания (ИЛИ-НЕ), а также логического умножения и отрицания (И-НЕ).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 308; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.118.95 (0.038 с.) |
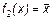 и называется отрицанием.
и называется отрицанием.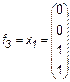 ,
, 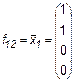 ,
, 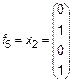 ,
, 
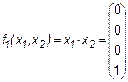 .
.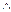 x 2.
x 2.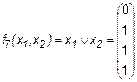 .
.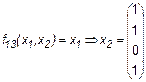 .
.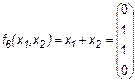 .
.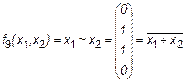 .
.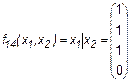 .
.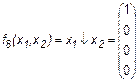 .
.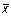 = 0, если х = 0, то
= 0, если х = 0, то 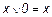 ;
;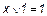 ;
;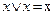 ;
;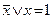 ;
;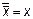 ;
;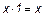 ;
;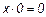 ;
;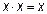 ;
;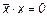 ;
;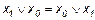 ;
;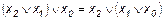 ;
;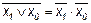 ;
;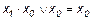 ;
;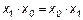 ;
;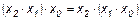 ;
;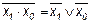 ;
;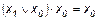 ;
;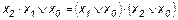 ;
;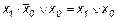 ;
;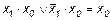
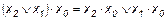 ;
;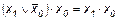 ;
;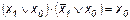
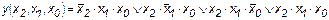 , (1.1)
, (1.1)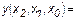
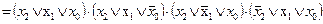 . (1.2)
. (1.2)