
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гидравлическое сопротивление двухфазных потоков⇐ ПредыдущаяСтр 30 из 30
Полный перепад давления. В инженерной практике используются, как правило, одномерные модели двухфазных потоков. Перепад давления в направлении оси канала z для одномерного двухфазного потока выражается уравнением: где D – гидравлический диаметр канала; g – проекция ускорения свободного падения на направление z. Первый член уравнения (8.57) отражает потери давления за счет ускорения потока, связанного либо с изменением паросодержания х, либо с изменением площади поперечного сечения канала S. При адиабатном течении в канале постоянного сечения этот член уравнения равен нулю. Второй и третий члены правой части уравнения (8.57) выражают соответственно потери давления на трение и на работу против массовых сил. При умеренных скоростях основной вклад в гидравлическое сопротивление вносят потери на трение. Гомогенная модель дает простой, физически ясный и дающий удовлетворительные результаты метод расчета значений где Формулу (8.58) можно представить в следующем виде: где
Согласно гомогенной модели потери на трение в двухфазном потоке с увеличением паросодержания растут линейно и при полном испарении жидкости (х = 1): Применение формул (8.58) и (8.59) оправдано в потоках с гомогенной структурой, т.е. при пузырьковом и эмульсионном режимах течения, при φ<0,7 при больших скоростях смеси. При малых скоростях смеси дают заниженные значения
Причем плотность смеси рассчитывается по формуле: а истинное паросодержание по формулам:
Гидравлическое сопротивление в дисперсно-кольцевом потоке. Для восходящего дисперсно-кольцевого режима течения справедливы соотношения:
где
Истинное объемное паросодержание определяется по формуле: если не учитывать расход жидкости в виде капель в газовом ядре. Касательное напряжение на стенке определяется по формуле: где Касательное напряжение по поверхности пленки определяется по формуле: Коэффициент трения на межфазовой поверхности можно рассчитывать по соотношению: где
Значение Так как восходящее кольцевое течение возможно при значительных скоростях газа Соотношения (8.63–8.68) позволяют рассчитывать истинное объемное паросодержание и гидравлическое сопротивление восходящего кольцевого газожидкого потока.
Решение уравнений (8.63) весьма громоздко, необходимость применения машинного счета очевидна. При больших приведенных скоростях газа для дисперсно-кольцевого режима течения справедливо эмпирическое соотношение: где
Формула (8.69) применима при условии, что Для пароводяных потоков истинное объемное паросодержание в дисперсном кольцевом режиме может быть найдено по номограмме.
Нормативный метод. Метод основан на использовании гомогенной модели при любых режимах течения, т.е. во всем диапазоне паросодержаний при На основе опытных данных для пароводяных потоков вводится относительный коэффициент гидравлического сопротивления ψ, а искомый перепад давления определяется по формуле: Значение ψ определяется по номограммам. Местные сопротивления в двухфазных потоках рассчитываются по формулам для гомогенного потока: где
8.7.5. Критические истечения двухфазных систем.
Для многих практических решений, в первую очередь для систем аварийной защиты АЭС, требуется рассчитывать скорость истечения двухфазного потока через отверстия или насадки. Наиболее важной является задача об истечении насыщенной или недогретой до температуры насыщения жидкости. Истечение такой жидкости сопровождается падением давления ниже локального давления насыщения, что приводит к парообразованию внутри канала. Наличие в потоке сжимаемой фазы создает условие для появления критического режима. Критические режимы истечения двухфазных потоков значительно отличаются от аналогичных режимов при истечении однофазной сжимаемой среды, где критический режим наступает при достижении в критическом сечении локальной скорости звука. В двухфазном потоке достижение максимального критического расхода смеси необязательно сопряжено с установлением в критическом сечении давления, независящего от противодавления, что характерно для однофазного истечения газового потока. В критическом сечении однофазного (газового) потока устанавливается скорость звука при определенном давлении. В двухфазном потоке само определение скорости звука не является однозначным. Причем, скорость звука зависит как от действительной структуры потока, так и от принятой физической модели процесса распространения волны возмущения. В настоящее время не сложилась еще общепринятая точка зрения на механизм истечения и возникновения критических режимов в двухфазных потоках. На основе обработки опытных данных по истечению насыщенной и недогретой до насыщения воды из коротких (L/D≤6) каналов небольшого диаметра (D≤9) для плотности потока может быть рекомендована следующая формула:
где
Отличие формулы (8.73) от формулы для однофазного потока состоит в том, что при определении плотности потока массы однофазной смеси используется перепад давлений По мере роста недогрева и снижения давления начального давления При давлениях если Для коротких каналов (L/D<6) большого сечения (D>9мм) расчет по приведенным формулам дает завышенный результат. В длинных каналах (L/D>6) при значительных недогревах ( где При критическом истечении углеводородов для длинных каналов (L/D>8) применяется критериальное уравнение: где безразмерные величины
где
Безразмерные длина и диаметр канала, входящие в параметр Уравнение (8.77) применимо в диапазоне π = 0,025÷0,52 (при этом Порядок расчета по уравнению (8.77) следующий: 1) задаемся значением 2) рассчитываем входной перегрев жидкости 3) рассчитываем левую и правую часть уравнения (8.77) с использованием выражений (8.78). Если расхождение между ними окажется значительным, то задаемся новым значением
4) проверяем, лежат ли значения
8.8. Движение одиночных капель и пузырьков 8.8.1. Методы подобия и размерностей
В механике двухфазных систем числа подобия могут быть представлены как мера отношения сил, действующих на единицу площади поверхности:
(8.81) (8.82) где
Число Рейнольдса можно представить как отношение сил
При анализе движения дискретной капли (частицы) в сплошной среде коэффициент сопротивления используется как число подобия в виде: где
При анализе двухфазных систем часто используется безразмерное число, содержащее лишь свойства фаз и ускорение свободного падения: С помощью чисел подобия процесс движения пузырьков можно описать уравнением вида: или Причем, во многих случаях движение дискретной фазы (внутри пузырька или капли) оказывается несущественным, так что симплексы Конкретный вид уравнения подобия может быть получен на основе опытных результатов, а в отдельных случаях и теоретически. Силы поверхностного натяжения стремятся придать пузырьку (капле) сферическую форму, а остальные силы стремятся его деформировать. Поэтому в общем случае неравенства:
можно рассматривать как условие сферичности пузырька (капли). Первое условие характерно для задач гидростатики, последнее – для движущихся капель и пузырьков (достаточное условие сферичности). При анализе размерностей всегда следует думать о физической полноте набора независимых параметров и переменных процесса. Иначе можно получить формально верный, но физически ошибочный результат. В качестве примера приведем эмпирическую формулу для скорости свободного всплытия газового пузыря в жидкости, когда эта скорость снижается с увеличением радиуса пузыря:
где
В формуле (8.88) размерности согласованы:
Однако в ней отсутствует подъемная сила В рамках анализа размерностей можно предположить, что: а) определяемым критерием подобия является отношение масштаба динамического сопротивления подъему пузыря в жидкости к масштабу силы Архимеда:
где
б) коэффициент гидравлического сопротивления представляет собой функцию деформации пузыря, характеризуемого отношением силы поверхностного натяжения и той же силы Архимеда. Безразмерное соотношение этих воздействий можно записать в форме:
где
8.8.2. Скорость движения капли и пузырька при Re <1
При малых числах Рейнольдса уравнение Навье–Стокса для несжимаемой жидкости упрощается, ибо в нем можно опустить инерционный член В таком приближении было получено решении задачи о движении сферической капли в вязкой жидкости при Решение дает поля скоростей во внешней области и внутри капли, а также значения нормальных и касательных напряжений на границе капли. Интеграл от проекций этих напряжений на направление движения можно рассматривать как силу сопротивления: где
Если Для капли, движущейся в жидкости под действием Архимедовой силы Для твердой сферы где В маловязких жидкостях (вода, керосин, спирты и т.п.) в газах условию 8.8.3. Скорость всплытия газового пузырька в жидкости
Свободный газовый пузырь в жидкости, или капля одной жидкости в другой жидкости при отсутствии эффекта смешения, имеет одну определенную геометрическую характеристику – объем V. Форма пузыря и его линейные характеристики могут изменяться под действием динамических сил и силы поверхностного натяжения на границе раздела фаз (компонент). Таким образом, в качестве линейного масштаба можно вводить или величину V1/3, или эффективный радиус: Свободное движение пузыря обусловлено подъемной силой порядка Определяемый критерий в форме числа Фруда: где В критериях надо брать модуль величины относительной плотности Обычно связь между подъемной силой и гидродинамическим сопротивлением записывают в форме, соответствующей стационарному обтеканию правильной сферы: При такой записи т.е. по существу, это один и тот же критерий подобия. Практически удобнее пользоваться корнем квадратным из критерия Фруда, который обозначим символом безразмерной скорости всплытия пузыря: На границе раздела возникает гидродинамическое взаимодействие, вызывающее образование поля давления. Это приводит к деформациям и осцимациям[2] поверхности пузыря. В качестве меры этой деформации поверхности раздела принимается критерий, характеризующий взаимодействие подъемной силы и давления, создаваемого поверхностным натяжением: Молекулярные вязкости жидкости и газа проявляются в условиях преобладания ламинарного характера течения, т.е. при относительно малых числах Рейнольдса: При этом следует учитывать критерий Архимеда: и симплекс[3] Если в пузыре существенно выражены динамические эффекты, то в качестве самостоятельной величины учитывается симплекс: В реальных ситуациях действие симплексов (8.102) и (8.9103) практически не проявляется. Для сферы с неподвижными границами вязкого обтекания (Re<1) имеем В области вязкого обтекания с отрывом (1<Re<5×102): В области первой автомодельности (5×102 <Re<105) соответствуют законы всплытия: Для малых пузырей (капель), сохраняющих строго сферическую форму, для области Re<1 имеется теоретическое решение Адамара-Рыбчинского, учитывающее подвижность границы раздела: При или Это известная формула Стокса для движения твердой сферы в жидкости. Общий характер зависимости
Рис. 8.13. Зависимость скорости всплытия пузырьков от их диаметра В реальных средах реализуется закон (8.108). Это обусловлено упрочнением границы раздела диффундирующими к ней примесями, имеющимися в жидкости и газе. При движении пузыря (капли) в канале, например круглой трубе, необходимо учитывать взаимодействие со стенками. С этой целью, при прочих равных условиях вводится отношение эффективного радиуса пузыря к внутреннему радиусу трубы. Общий характер зависимости Правая ветвь, имеющая отчетливый минимум, соответствует движению деформирующихся больших пузырей и практически автомодельна относительно вязкости, т.е. критерия Установлено, что с помощью критериев подобия опытные данные по скоростям всплытия газовых пузырьков в различных жидкостях не удается обобщить единой зависимостью. Поэтому, можно выделить пять характерных зон на зависимости скорости всплытия На рис.8.13 границы зоны отмечены для дистиллированной воды. Зона I –сферические пузырьки при Re<1, Скорость всплытия подчиняется в чистых жидкостях при условии, что Малые газовые пузырьки в воде ( Зона II –сферические пузырьки при Re>1. Приближенно можно принимать, что сферичность сохраняется при При Рейнольдсе от 1 до 40 можно пользоваться формулой Чао: Зона III – пузырьки, сплющенные вдоль вертикальной оси в виде сфероидов. Эта зона ограничена условием Зона IV – пузырьки неправильной формы, всплытие которых происходит по сложной винтообразной траектории и сопровождается пульсациями формы. Для нижней границы Для воды скорость всплытия Зона V – пузырьки объемом V>2 см3, имеющие форму практически правильного сферического сегмента. Пузырьки в жидкостях любой вязкости всплывают со скоростью:
При этом возможно дробление пузырьков в маловязких жидкостях.
8.8.4. Особенности движения капель в газовых потоках
Малые сферические капли жидкости при Re<1 имеют скорость падения в газе, определяемую формулой Стокса:
при Условию Re<1 подчиняется падение в газе капель диаметром не более 0,1 мм. При 0,5 ≤ Re ≤ 5 скорость падения капель в газе определяется с помощью формулы Озеена для коэффициента сопротивления: Эта формула получена для движения твердой сферы в жидкости при частичном учете влияния инерционных членов в уравнении Навье-Стокса. При больших числах Рейнольдса движение капли в газе сопровождается отрывом потока в кормовой части ее поверхности для сферической капли при Re>>1 (практически при Re>20). Скорость падения определяется по формуле: Верхняя граница применимости этой формулы определяется условием Согласно этой формулы капля воды, падая в воздухе при комнатной температуре, сохраняет сферичность при диаметре 2R<1,5 мм. При где В газовых потоках скорость падения капель На основе опытных данных при условии:
происходит дробление капель. Это условие отвечает предельному диаметру капель:
где
8.8.5. Схлопывание (расширение) полости в жидкости. Уравнение Рэлея
Задача о схлопывании (расширении) с
|
|||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 426; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.33.41 (0.167 с.) |
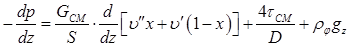 (8.57)
(8.57) – касательное напряжение на стенке канала при течении смеси;
– касательное напряжение на стенке канала при течении смеси; СМ. Тогда:
СМ. Тогда: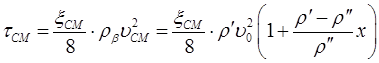 (8.58)
(8.58)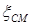 – коэффициент трения в пузырьковом, снарядном и эмульсионном режимах течения рассчитывается как для однофазного потока по формулам Блазиуса, Конакова, Шифринсона, Никурадзе и Альтшуля. При этом число Рейнольдса можно приближенно рассчитывать как
– коэффициент трения в пузырьковом, снарядном и эмульсионном режимах течения рассчитывается как для однофазного потока по формулам Блазиуса, Конакова, Шифринсона, Никурадзе и Альтшуля. При этом число Рейнольдса можно приближенно рассчитывать как  . При турбулентном течении удовлетворительные результаты получаются, если принять
. При турбулентном течении удовлетворительные результаты получаются, если принять  (8.59)
(8.59) – касательное напряжение на стенке при течении в том же канале однофазной жидкости с расходом GCM;
– касательное напряжение на стенке при течении в том же канале однофазной жидкости с расходом GCM;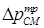 ,
, 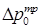 – перепады давления в канале за счет трения в двухфазном и однофазном потоках (
– перепады давления в канале за счет трения в двухфазном и однофазном потоках (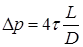 , где L – длина канала, D – диаметр канала).
, где L – длина канала, D – диаметр канала).
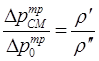 (8.60)
(8.60)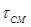 . Лучший результат достигается при расчете
. Лучший результат достигается при расчете  (8.61)
(8.61)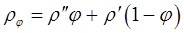 (8.62)
(8.62)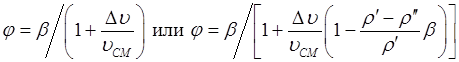 .
.
 (8.63)
(8.63) и
и 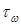 – касательные напряжения на свободной поверхности пленки и на стенке соответственно;
– касательные напряжения на свободной поверхности пленки и на стенке соответственно; – толщина пленки;
– толщина пленки;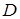 – диаметр канала.
– диаметр канала.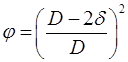 (8.64)
(8.64)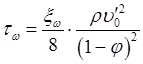 (8.65)
(8.65)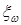 – коэффициент трения на границе жидкая пленка–стенка, определяемый по формулам однофазного потока в зависимости от
– коэффициент трения на границе жидкая пленка–стенка, определяемый по формулам однофазного потока в зависимости от 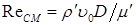 .
.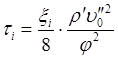 (8.66)
(8.66)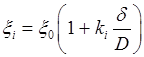 (8.67)
(8.67)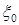 – коэффициент трения газового потока в гладком канале, определяемый по значениям Рейнольдса
– коэффициент трения газового потока в гладком канале, определяемый по значениям Рейнольдса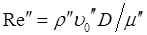
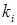 принимается равным 300.
принимается равным 300. в большинстве случаев можно принять
в большинстве случаев можно принять 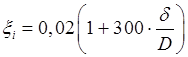 (8.68)
(8.68)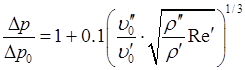 (8.69)
(8.69) – перепад давления в двухфазном потоке;
– перепад давления в двухфазном потоке; – перепад давления в однофазном потоке жидкости, имеющей скорость
– перепад давления в однофазном потоке жидкости, имеющей скорость 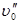 .
. и ламинарном течении жидкости в пленке. При этом для расчета истинного объемного паросодержания используется формула:
и ламинарном течении жидкости в пленке. При этом для расчета истинного объемного паросодержания используется формула: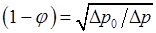 (8.70)
(8.70) .
.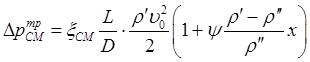 (8.71)
(8.71) (8.72)
(8.72)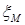 – коэффициент местного сопротивления, определяется из таблиц или нормативных документов.
– коэффициент местного сопротивления, определяется из таблиц или нормативных документов.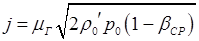 (8.73)
(8.73)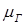 – гидравлический коэффициент расхода, который для каналов с острой кромкой на входе равен 0,61;
– гидравлический коэффициент расхода, который для каналов с острой кромкой на входе равен 0,61; и
и 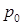 – плотность и давление заторможенного потока на уровне входного отверстия;
– плотность и давление заторможенного потока на уровне входного отверстия;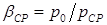 , здесь
, здесь 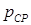 – давление на выходном срезе канала.
– давление на выходном срезе канала.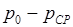 , а не полная разность между давлением
, а не полная разность между давлением 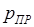 .
.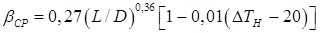 (8.74)
(8.74) К, а при
К, а при 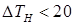 К – по формуле
К – по формуле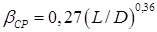 (8.75)
(8.75)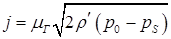 (8.76)
(8.76)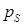 – давление насыщения при температуре Т0.
– давление насыщения при температуре Т0.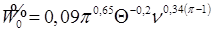 (8.77)
(8.77)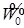 ,
, 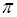 ,
, 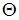 ,
,  выражены с помощью масштабов, полученных с использованием молекулярной массы m индивидуальной газовой постоянной R, давления и температуры в критической точке рКР, ТКР:
выражены с помощью масштабов, полученных с использованием молекулярной массы m индивидуальной газовой постоянной R, давления и температуры в критической точке рКР, ТКР: (8.78)
(8.78)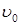 - скорость жидкости на входе в канал, отнесенная к полному сечению канала;
- скорость жидкости на входе в канал, отнесенная к полному сечению канала;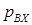 – давление на входе в канал, определяемое по формуле
– давление на входе в канал, определяемое по формуле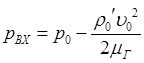 (8.79)
(8.79) – перегрев жидкости на входе в канал.
– перегрев жидкости на входе в канал.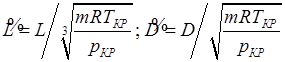
 может превышать 0,6);
может превышать 0,6);  .
. и по формуле (8.79) находим
и по формуле (8.79) находим 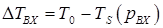 . Если получим
. Если получим 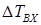 <0, то задаемся большим значением
<0, то задаемся большим значением 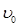 ;
; и
и 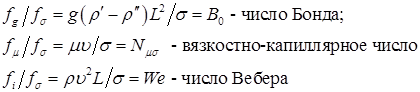 (8.80)
(8.80)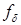 ,
, 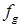 ,
, 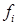 ,
, 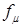 – соответственно силы поверхностного натяжения, гравитационные (архимедовы), инерции и вязкости;
– соответственно силы поверхностного натяжения, гравитационные (архимедовы), инерции и вязкости;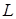 – характерный размер системы;
– характерный размер системы;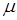 – динамическая вязкость жидкости;
– динамическая вязкость жидкости;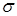 – коэффициент поверхностного натяжения;
– коэффициент поверхностного натяжения; и
и 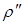 – плотность жидкости и газа;
– плотность жидкости и газа;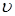 – характерная скорость;
– характерная скорость; – ускорение силы тяжести.
– ускорение силы тяжести. – инерции
– инерции 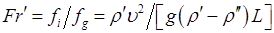 – для двухфазных систем, если в жидкости движется газовый пузырек.
– для двухфазных систем, если в жидкости движется газовый пузырек. – если капля движется в газе.
– если капля движется в газе.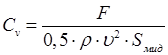 (8.83)
(8.83)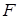 – сила вызывающая движение;
– сила вызывающая движение;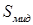 – площадь миделевого сечения частицы. Например, при движении в жидкости сферического пузырька коэффициент сопротивления аналогичен по физическому смыслу числу Фруда
– площадь миделевого сечения частицы. Например, при движении в жидкости сферического пузырька коэффициент сопротивления аналогичен по физическому смыслу числу Фруда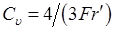 (8.84)
(8.84) (8.85)
(8.85)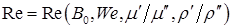 (8.86)
(8.86) (8.87)
(8.87) ,
, 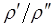 в анализе не учитываются.
в анализе не учитываются.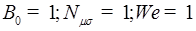
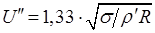 (8.88)
(8.88)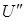 – скорость всплытия пузыря, м/с;
– скорость всплытия пузыря, м/с;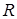 – радиус эквивалентной по объему сферы, м.
– радиус эквивалентной по объему сферы, м.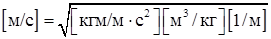 .
.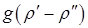 – единственный источник движения пузыря. Следовательно, независимо от действия гравитации пузырь по этой формуле всегда будет всплывать с одной и той же скоростью, даже в невесомости.
– единственный источник движения пузыря. Следовательно, независимо от действия гравитации пузырь по этой формуле всегда будет всплывать с одной и той же скоростью, даже в невесомости.
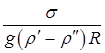
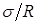 – мера давления, создаваемая поверхностным натяжением, Н/м2.
– мера давления, создаваемая поверхностным натяжением, Н/м2.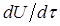 .
. .
.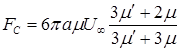 (8.89)
(8.89) – радиус капли;
– радиус капли;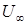 – скорость движения;
– скорость движения;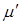 ,
, 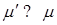 , то (8.86) переходит в формулу Стокса для обтекания твердой сферы при
, то (8.86) переходит в формулу Стокса для обтекания твердой сферы при 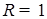 :
: (8.90)
(8.90)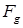 , равенство
, равенство 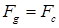 дает скорость её установившегося падения (всплытия):
дает скорость её установившегося падения (всплытия):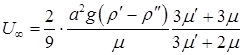 (8.91)
(8.91)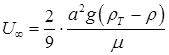 (8.92)
(8.92)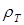 – плотность твердой фазы.
– плотность твердой фазы.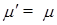 , так что:
, так что: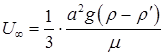 (8.93)
(8.93)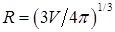 (8.94)
(8.94)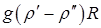 и силой гидродинамического сопротивления порядка
и силой гидродинамического сопротивления порядка 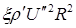 , здесь
, здесь  – коэффициент гидродинамического сопротивления пузыря;
– коэффициент гидродинамического сопротивления пузыря; 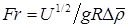 (8.95)
(8.95)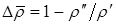 – относительная разность плотностей.
– относительная разность плотностей.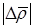 . Если
. Если  , то пузырь (капля) всплывает, если
, то пузырь (капля) всплывает, если 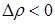 – капля тонет.
– капля тонет.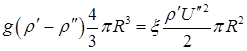 (8.96)
(8.96)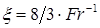 , (8.97)
, (8.97)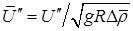 (8.98)
(8.98)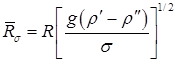 (8.99)
(8.99)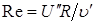 (8.100)
(8.100) (8.101)
(8.101)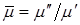 (8.102)
(8.102)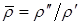 (8.103)
(8.103) (8.104)
(8.104)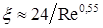 (8.105)
(8.105)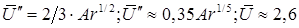 (8.106)
(8.106)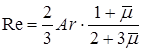 (8.107)
(8.107)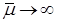 , т.е. при неподвижной (отвердевшей) границе раздела:
, т.е. при неподвижной (отвердевшей) границе раздела: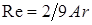 (8.108)
(8.108)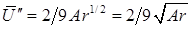 (8.109)
(8.109)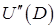 показан на рис. 8.13
показан на рис. 8.13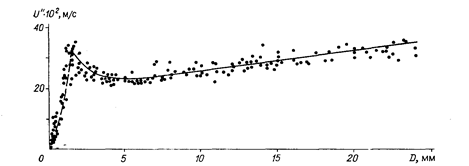
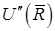 при свободном всплытии пузыря показан на рис.8.13. Левая ветвь отвечает малодеформированным сферам, т.е. автомодельна относительно
при свободном всплытии пузыря показан на рис.8.13. Левая ветвь отвечает малодеформированным сферам, т.е. автомодельна относительно 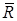 .
.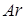 , т.е.:
, т.е.: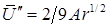 (8.110)
(8.110)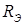 , которые для различных жидкостей охватывают различные диапазоны
, которые для различных жидкостей охватывают различные диапазоны  (8.111)
(8.111)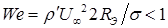 (8.112)
(8.112)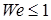 . При
. При  для газовых пузырьков Re = 300÷400,
для газовых пузырьков Re = 300÷400, 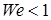 , автоматически приводит к требованию Re<1. в минеральном масле
, автоматически приводит к требованию Re<1. в минеральном масле 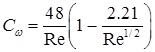 (8.114)
(8.114)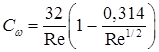 (8.115)
(8.115)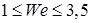 и охватывает весьма узкий диапазон размеров пузырьков (для воды
и охватывает весьма узкий диапазон размеров пузырьков (для воды 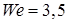 , для верхней
, для верхней 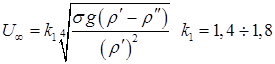 (8.116)
(8.116)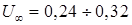 м/с.
м/с.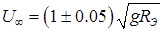 .
.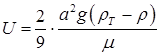
 ;
;  ;
;  .
.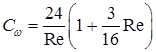 (8.117)
(8.117) (8.118)
(8.118) (8.119)
(8.119)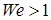 капли деформируются, причем в определенной области размеров увеличение архимедовой силы с ростом объема капли компенсируется ростом силы сопротивления за счет большего её сплющивания, поэтому скорость падения остается неизменной:
капли деформируются, причем в определенной области размеров увеличение архимедовой силы с ростом объема капли компенсируется ростом силы сопротивления за счет большего её сплющивания, поэтому скорость падения остается неизменной: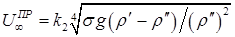 (8.120)
(8.120)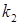 =1,6÷1,8, что соответствует
=1,6÷1,8, что соответствует 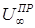 =7,6÷8,6 м/с для капель воды в воздухе.
=7,6÷8,6 м/с для капель воды в воздухе.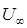 есть скорость движения капель относительно газа. При подъемном движении газа значение
есть скорость движения капель относительно газа. При подъемном движении газа значение  , где
, где 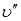 – скорость газа, подъемное движение которого соответствует положительному направлению системы отсчета.
– скорость газа, подъемное движение которого соответствует положительному направлению системы отсчета.
 ,
,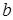 – капиллярная постоянная:
– капиллярная постоянная: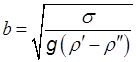 (8.121)
(8.121)


