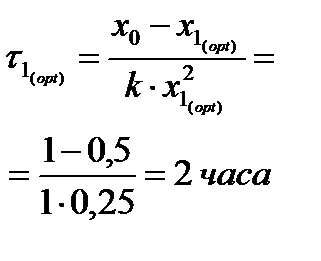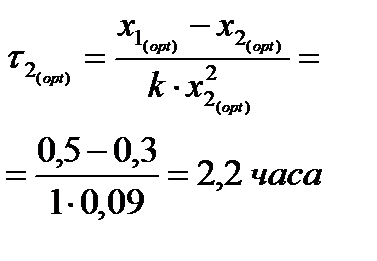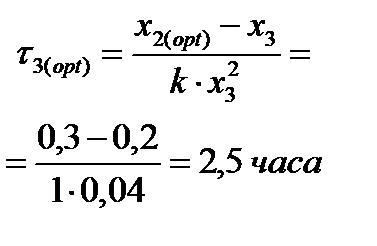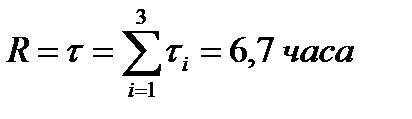Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулировка принципа оптимальностиБелмана
Оптимальная стратегия обладает таким свойством, что каково бы ни было начальное состояние и начальное решение, последующие решения должны приниматься, исходя из оптимальной стратегии относительно состояния, получаемого в результате первого решения Общая схема решения задач методом динамического программирования При подходе к решению задач оптимизации методом динамического программирования необходимо обращать внимание на следующее: a) оптимизируемый процесс должен быть дискретно-распределённым во времени или пространстве (многостадийный процесс); b) отдельные стадии процесса должны обладать относительной независимостью, т.е. вектор выходных параметров любой стадии должен зависеть только от вектора входных параметров на эту стадию и управлений на ней; c) критерий оптимальности процесса должен быть сформулирован как аддитивная функция критериев оптимальности каждой стадии; При выполнении перечисленных условий необходимо правильно формулировать задачу оптимизации. При формулировке должны быть выявлены: • параметры, характеризующие состояние каждой стадии; • управляющие параметры на каждой стадии; • ограничения, которые накладываются на параметры состояния процесса и управляющие параметры. Необходимо составить: 1. математическое описание для каждой стадии (рис.1.7.4); 2. критерий оптимальности.
её состоянием:
параметров и вектором управлений: Первый этап решения
экстремальным (например, максимальным):
предыдущей стадии
где математическая модель предыдущей стадии имеет вид: с зависимостями для управляющихпеременных:
для данной стадии, получим:
откуда определяется оптимальное управление
С учётом φ i получим математическую формулировку принципа оптимальности, являющуюся рекуррентной формулой,
решение задачи оптимизации последовательно:
Для первой стадии имеем:
А)или В) более сложная задача (большей размерности). На этом завершается 1-этап решения задачи ДП.
и (i=2,…N):
Произвольная стадия каскада
Пример 1.
Задана конечная концентрация A: Число реакторов в каскаде N. Задача оптимизации: выбрать объёмы реакторов так, чтобы суммарный объём всех реакторов был минимальным. Нетрудно видеть, что в поставленной задаче оптимизации выполнены условия a, b и с: оптимизируемый процесс является дискретно-распределённым в пространстве; отдельные стадии процесса обладают относительной независимостью (выход каждого реактора зависит только от входящих переменных и управлений на нём) и критерий оптимальности всего процесса является аддитивной функцией частных критериев (критерий оптимальности - объём каскада реакторов, частные критерии - объёмы каждого аппарата). Запишем сведения о процессе, необходимые для решения задачи оптимизации: Параметрами, характеризующими состояние каждой стадии являются концентрации продукта реакции или исходного реагента - xi.
На параметры состояния процесса на каждой стадии наложены ограничения:
Составляем критерий оптимальностиили Пример 1.
где
Концентрация реагента A на выходе из реактора N однозначно определяет время пребывания в нём, поэтому именно её можно взять в качестве управляющего параметра. Тогда задача оптимизации на последней стадии состоит в выборе такой концентрации на выходе из N –го аппарата, при которой время пребывания в N –ом аппарате было бы минимальным. Однако в рассматриваемой задаче конечная концентрация xN задана, поэтому задача какого-либо выбора исключается и остаётся только рассчитать время пребывания
к предпоследнему реактору: Если вид выражения критерия не сложен, а названное управление - это единственный управляющий параметр, то для определения экстремума r*N на стадии можно пользоваться теоремами математического анализа. Если же выражение критерия сложно, а управление есть совокупность нескольких управляющих воздействий, то решение с использованием классического дифференциального анализа или невозможно, или представляет значительные трудности. Поэтому следует применять методы нелинейного программирования.
воспользовавшись необходимым условием существования экстремума функции одной переменной:
Из последнего выражения следует:
Следовательно:
Чтобы получить минимальное значение времени пребывания в двух последних реакторах, запишем рекуррентное соотношение:
рекуррентное соотношение: Найдём минимум, воспользовавшись необходимым условием существования экстремума функции одной переменной:
Проверим достаточное условие:
последнее выражение полученное значение оптимальной концентрации, имеем:
Подставив значение оптимальной концентрации в рекуррентное соотношение, получим:
Решение задачи выполняется таким же образом последовательно для всех реакторов до первого включительно.
и рекуррентного соотношения:
и для первого реактора:
ВТОРОЙ ЭТАП РЕШЕНИЯ
Далее определяется:
Далее определяется: и т.д. до тех пор, пока не будут получены значения всех оптимальных управлений.
Пример 2 В каскаде реакторов идеального перемешивания проводится простая реакция 2-го порядка: A → P. Каждый из аппаратов каскада работает в изотермических условиях, причём температура реакционной массы во всех аппаратах одинакова. Требуется определить среднее время пребывания реакционной массы в каждом из аппаратов с тем, чтобы общее время пребывания реакционной массы в системе было минимальным. Исходные данные: Число аппаратов N = 3 Начальная концентрация компонента Ax 0 = 1 моль/литр
Константа скорости реакции:
Критерий оптимальности процесса по условию задачи есть:
Из уравнения материального баланса
Первый этап решения
Поскольку x 3 задано,
Рис.1.7.5. Функциональное уравнение
соотношение (рис.1.7.6.) для f 2:
Записываем рекуррентное соотношение (рис.1.7.7.) для f 3:
Рис.1.7.7. Рекуррентное соотношение для f 3.
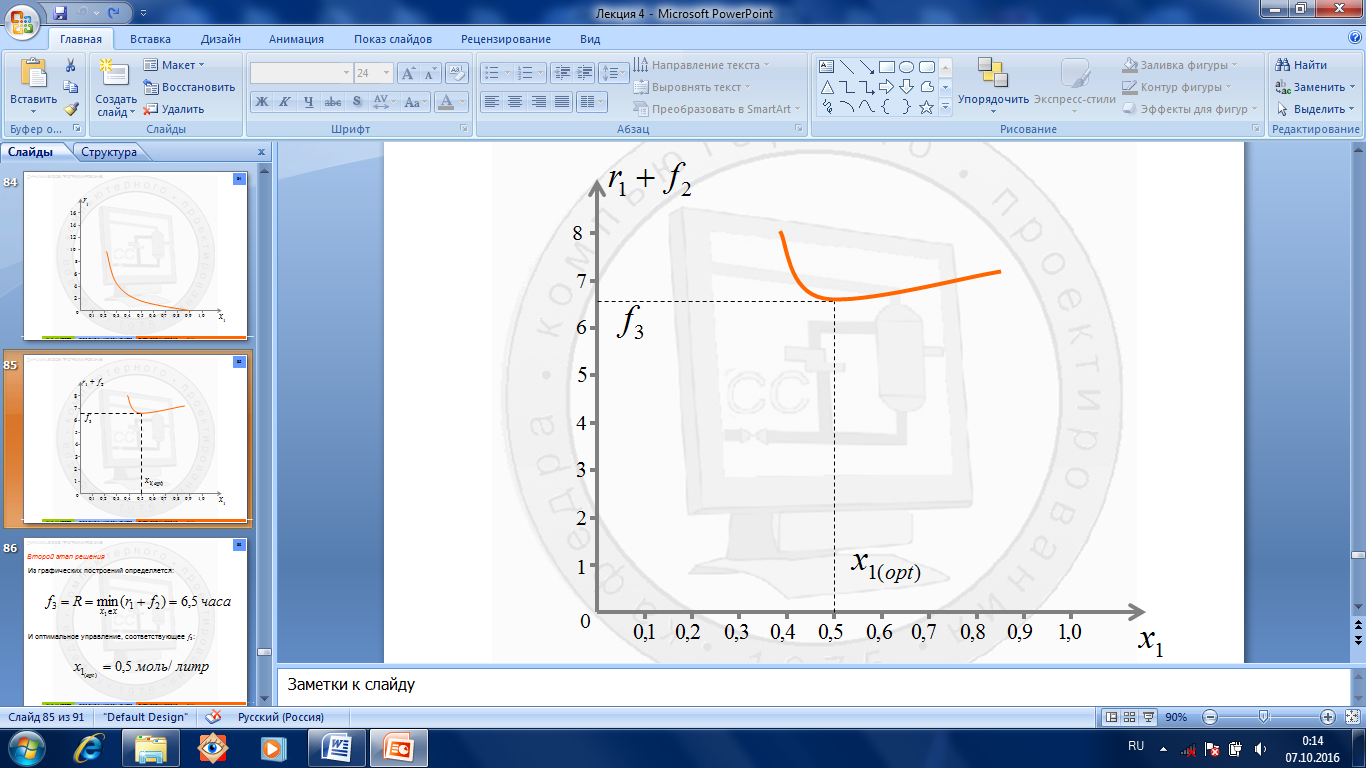
И оптимальное управление, соответствующее f 3:
графически определяем x 2( opt ): Рассчитываем время пребывания в каждом из аппаратов:
Небольшое расхождение τ = 6,7 часа с f 3 = 6,5 часа объясняется погрешностью графического расчёта.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 107; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.169.86 (0.082 с.) |
|||||||||||||||||||||||
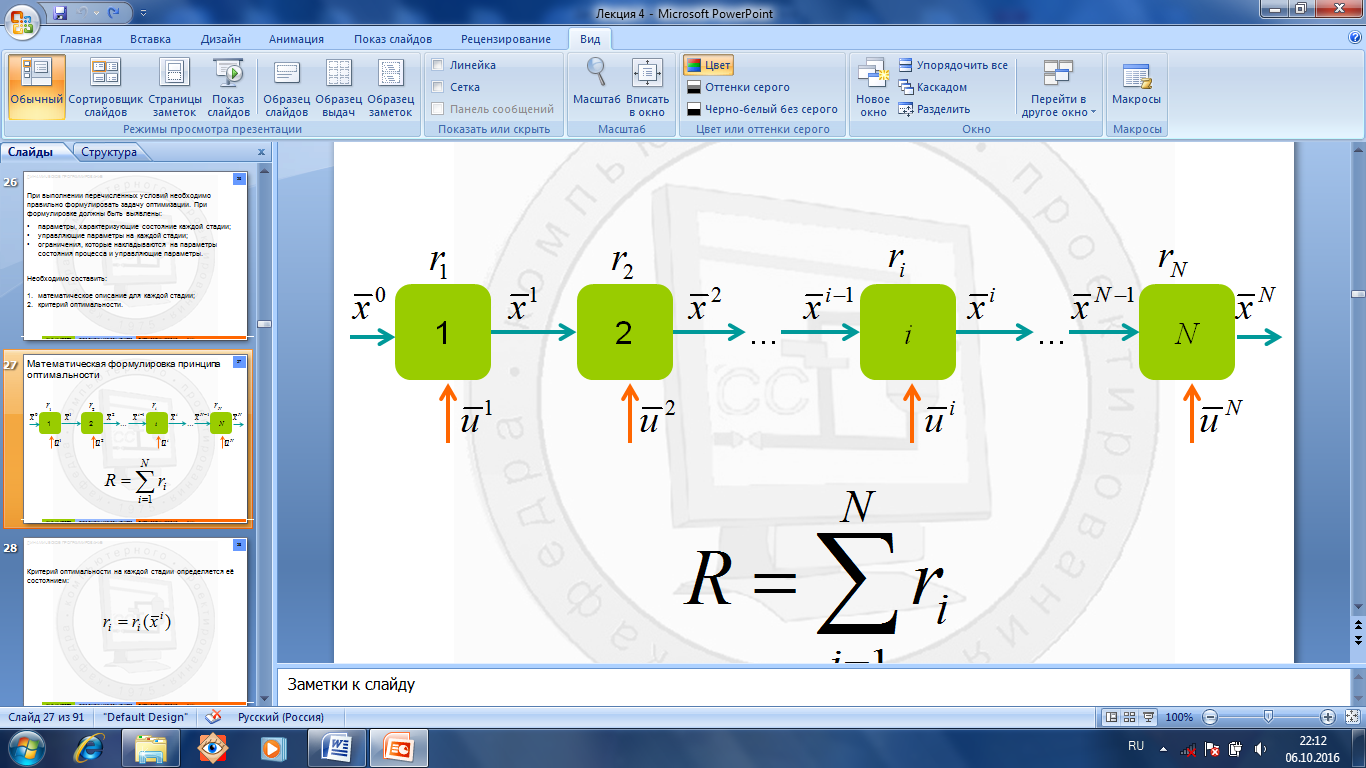
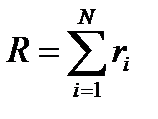 Рис.1.7.4. Стадии процеса
Рис.1.7.4. Стадии процеса Критерий оптимальности на каждой стадии определяется
Критерий оптимальности на каждой стадии определяется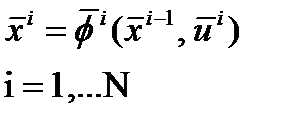 Уравнение математической модели для i –й стадии даёт связь между вектором входных параметров, вектором выходных
Уравнение математической модели для i –й стадии даёт связь между вектором входных параметров, вектором выходных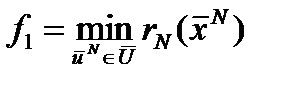 Решение задачи начинается с последней стадии, где необходимо выбрать оптимальное управление – так, чтобы
Решение задачи начинается с последней стадии, где необходимо выбрать оптимальное управление – так, чтобы критерий оптимальности rN был
критерий оптимальности rN был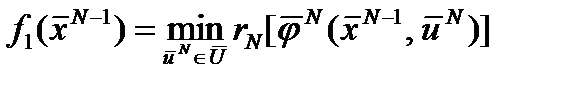 Используя уравнение математической модели для данной стадии, получим:
Используя уравнение математической модели для данной стадии, получим:
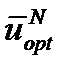 откуда определяется оптимальное
откуда определяется оптимальное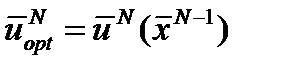 управление которое зависит от выходных переменных
управление которое зависит от выходных переменных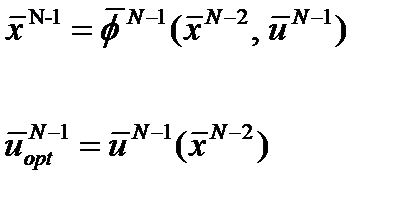
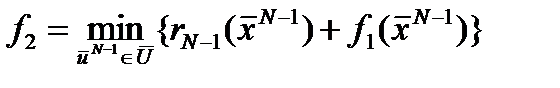 Переходя к стадии N – 1, получим условие выбора оптимального уравнения:
Переходя к стадии N – 1, получим условие выбора оптимального уравнения: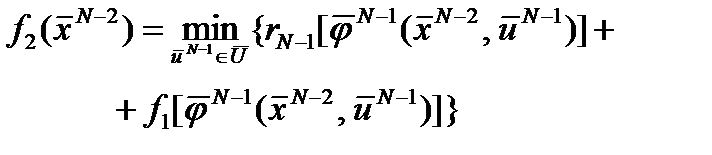 Поскольку f 1 уже выбрано, определение f 2 даёт возможность выбора оптимального управления на стадии N – 1. Подставляя уравнение математической модели
Поскольку f 1 уже выбрано, определение f 2 даёт возможность выбора оптимального управления на стадии N – 1. Подставляя уравнение математической модели
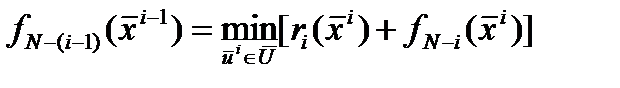
 Проводя аналогичный анализ, для стадии i можно записать:
Проводя аналогичный анализ, для стадии i можно записать: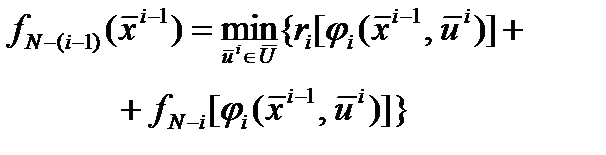 позволяющей выполнять
позволяющей выполнять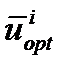 где fN -(i -1) – значение суммы критериев оптимальности последних N -i стадий, откуда определяется оптимальное управление
где fN -(i -1) – значение суммы критериев оптимальности последних N -i стадий, откуда определяется оптимальное управление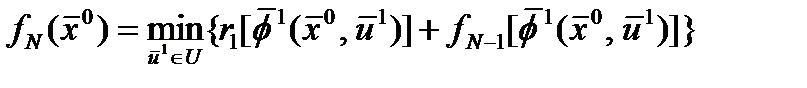
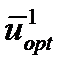
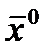
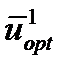 откуда определяется оптимальное управление (А) или наряду с оптимальным управлением и оптимальные входные переменные (В):
откуда определяется оптимальное управление (А) или наряду с оптимальным управлением и оптимальные входные переменные (В):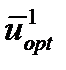 Второй этап решения
Второй этап решения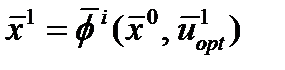
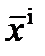
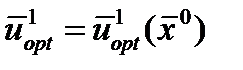
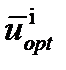 Для реализация 2-этапа на основе знания и по соотношениям, приведенным ниже, последовательно определяются (i=1,…N)
Для реализация 2-этапа на основе знания и по соотношениям, приведенным ниже, последовательно определяются (i=1,…N)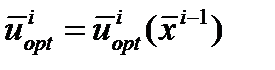
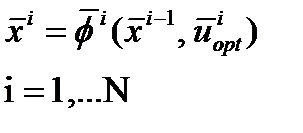
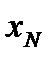
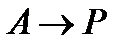 Пусть имеется каскад химических реакторов идеального перемешивания, в котором проводится необратимая реакция первого порядка:
Пусть имеется каскад химических реакторов идеального перемешивания, в котором проводится необратимая реакция первого порядка: Управляющие параметры - объёмы каждого реактора или, что то же самое, время пребывания смеси в каждом реакторе U i (при постоянной нагрузке).
Управляющие параметры - объёмы каждого реактора или, что то же самое, время пребывания смеси в каждом реакторе U i (при постоянной нагрузке).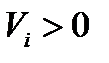
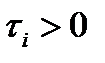 на параметры управления процесса на каждой стадии наложены ограничения:или
на параметры управления процесса на каждой стадии наложены ограничения:или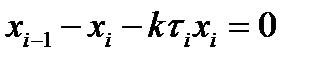
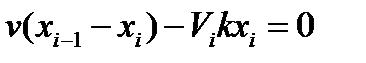 Составляем математическое описание каждой i-ой стадии (уравнение материального баланса):
Составляем математическое описание каждой i-ой стадии (уравнение материального баланса):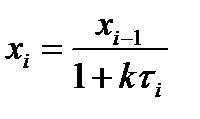 или
или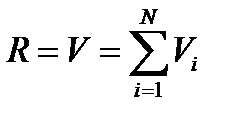
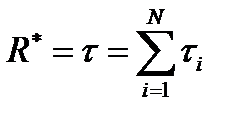 Откуда имеем:
Откуда имеем: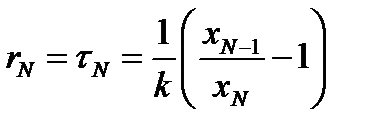
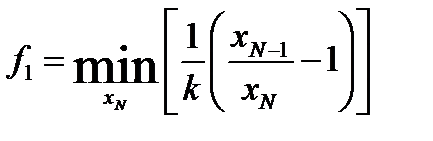 ПЕРВЫЙ ЭТАП решения выглядит следующим образом:
ПЕРВЫЙ ЭТАП решения выглядит следующим образом: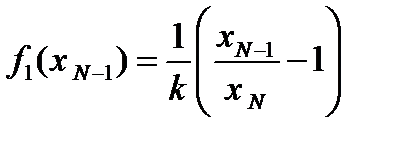 при заданном значении xN:
при заданном значении xN: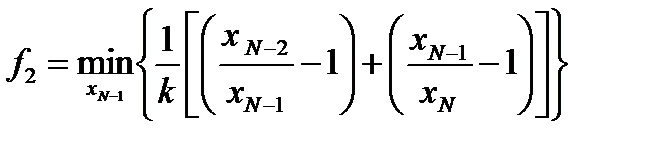 В соответствии с общей схемой переходим
В соответствии с общей схемой переходим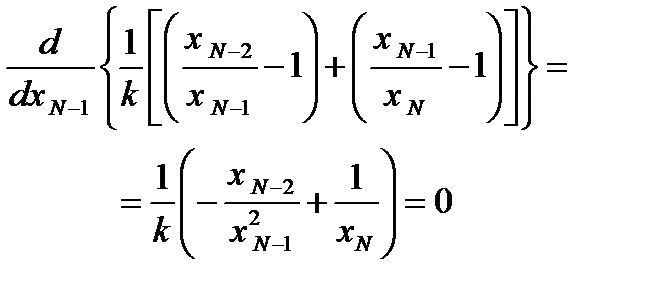 В предпоследнем реакторе необходимо выбрать такое значение xN -1, чтобы выражение в скобках имело минимум при любых значениях xN -2. Это значение xN -1 можно найти,
В предпоследнем реакторе необходимо выбрать такое значение xN -1, чтобы выражение в скобках имело минимум при любых значениях xN -2. Это значение xN -1 можно найти,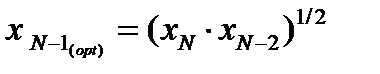
 Поскольку функция f 2 дифференцируемая, легко проверить достаточное условие существования экстремума:
Поскольку функция f 2 дифференцируемая, легко проверить достаточное условие существования экстремума: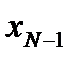 во всём диапазоне изменения xN -1,
во всём диапазоне изменения xN -1,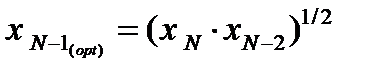 следовательно в точке
следовательно в точке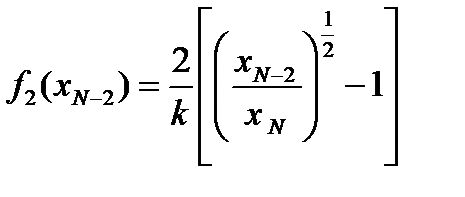 функция f 2 принимает минимальное значение.
функция f 2 принимает минимальное значение.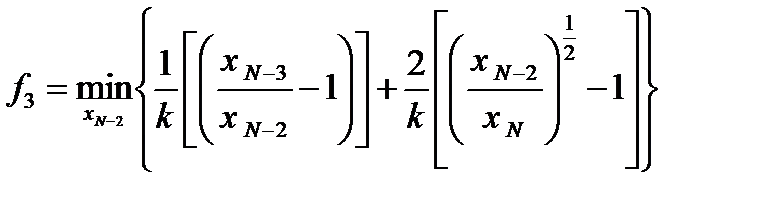 Повторим рассмотренную процедуру для третьего от конца реактора. Запишем для него
Повторим рассмотренную процедуру для третьего от конца реактора. Запишем для него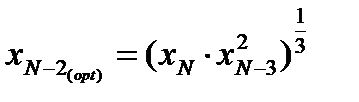
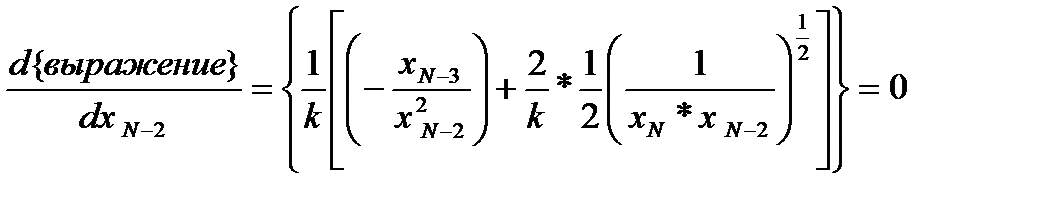
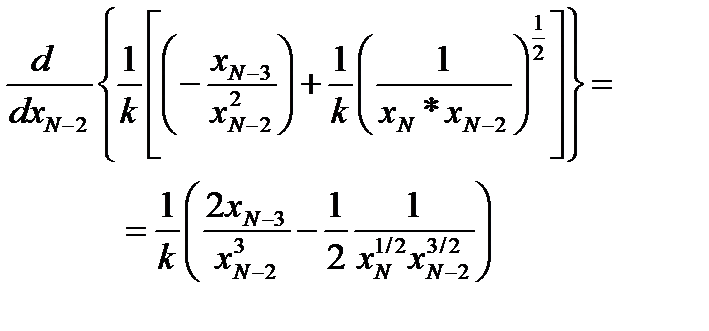 Откуда получаем:
Откуда получаем: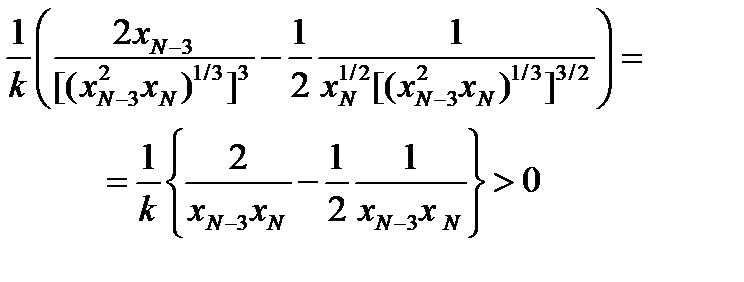 Подставив в
Подставив в т.е. при оптимальном значении концентрации действительно достигается минимум.
т.е. при оптимальном значении концентрации действительно достигается минимум. или после преобразований:
или после преобразований: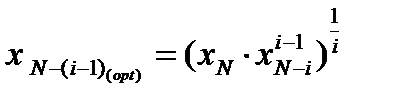 Для произвольного реактора i, считая от конца процесса, получим аналогичные выражения
Для произвольного реактора i, считая от конца процесса, получим аналогичные выражения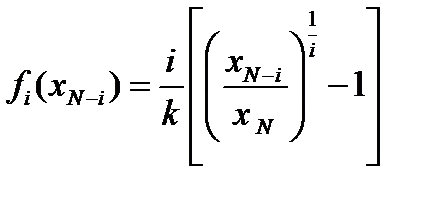 оптимальной концентрации:
оптимальной концентрации: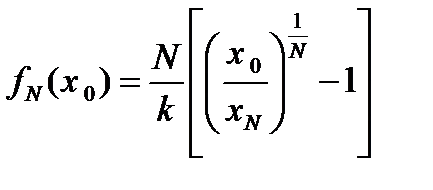
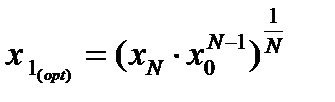 Для первого реактора:
Для первого реактора: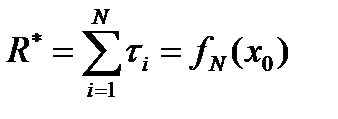 Поскольку в условии задачи x 0 и xN заданы, k и N неизвестны, из последнего выражения рассчитывается
Поскольку в условии задачи x 0 и xN заданы, k и N неизвестны, из последнего выражения рассчитывается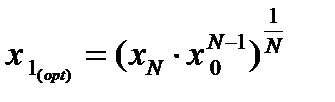 минимальное значение критерия оптимальности:
минимальное значение критерия оптимальности: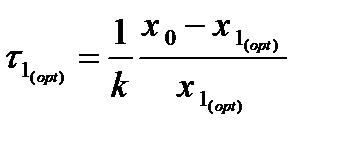
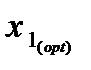 На втором этапе решения из полученных соотношений определяются:
На втором этапе решения из полученных соотношений определяются: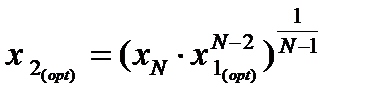
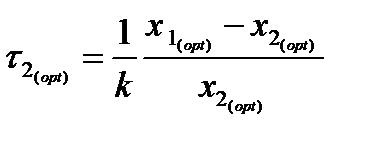 Для второго реактора имеем:
Для второго реактора имеем: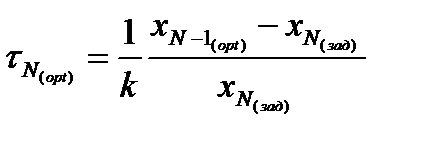 и т.д. до тех пор, пока не будут получены значения всех оптимальных управлений.
и т.д. до тех пор, пока не будут получены значения всех оптимальных управлений.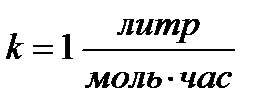 Конечная концентрация компонента A на выходе из каскада x 3 = 0,2 моль/литр
Конечная концентрация компонента A на выходе из каскада x 3 = 0,2 моль/литр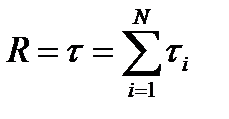 Решение
Решение τ i - среднее время пребывания в i – ом аппарате.
τ i - среднее время пребывания в i – ом аппарате.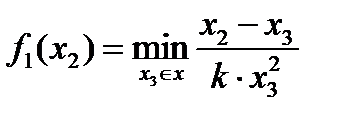 для i – го реактора имеем:
для i – го реактора имеем: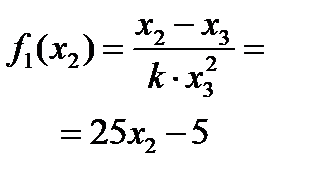 Записываем рекуррентное соотношение:
Записываем рекуррентное соотношение: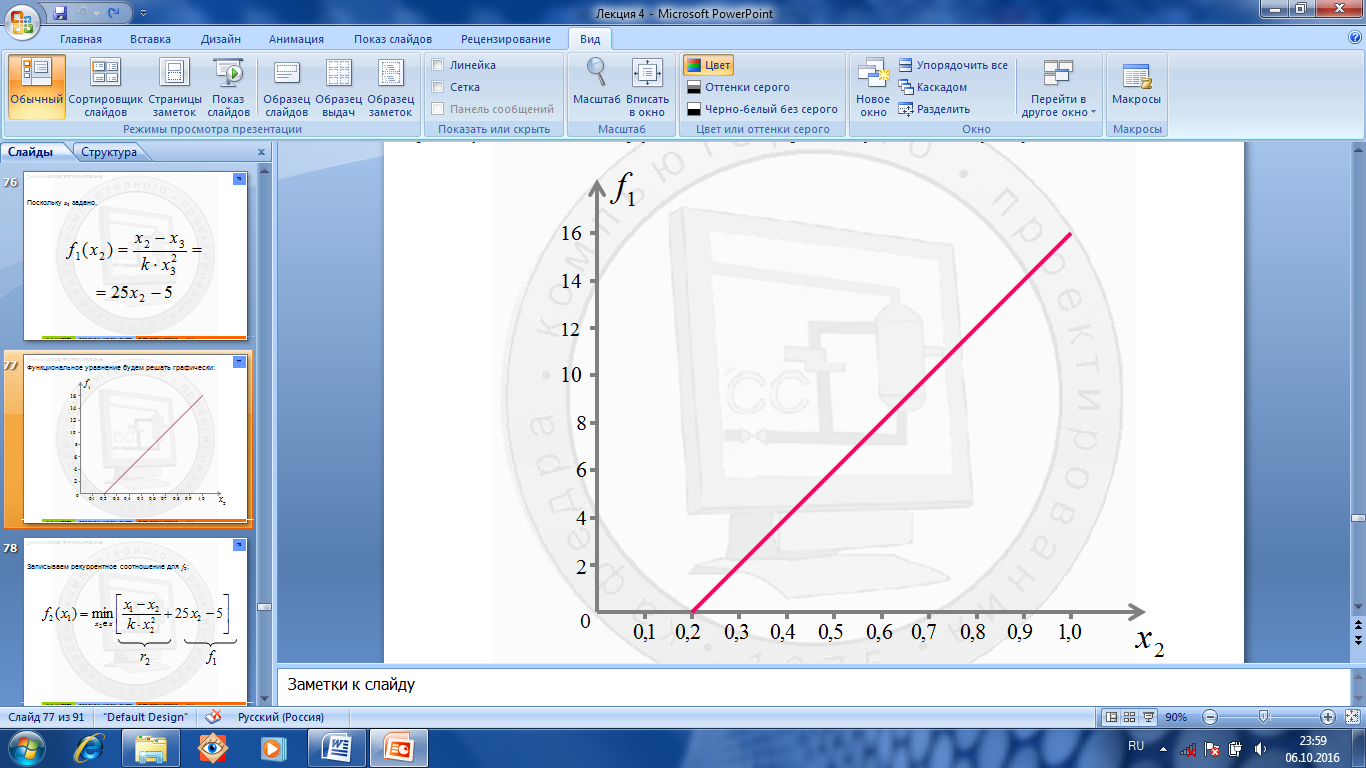
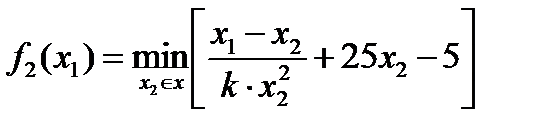 Записываем рекуррентное
Записываем рекуррентное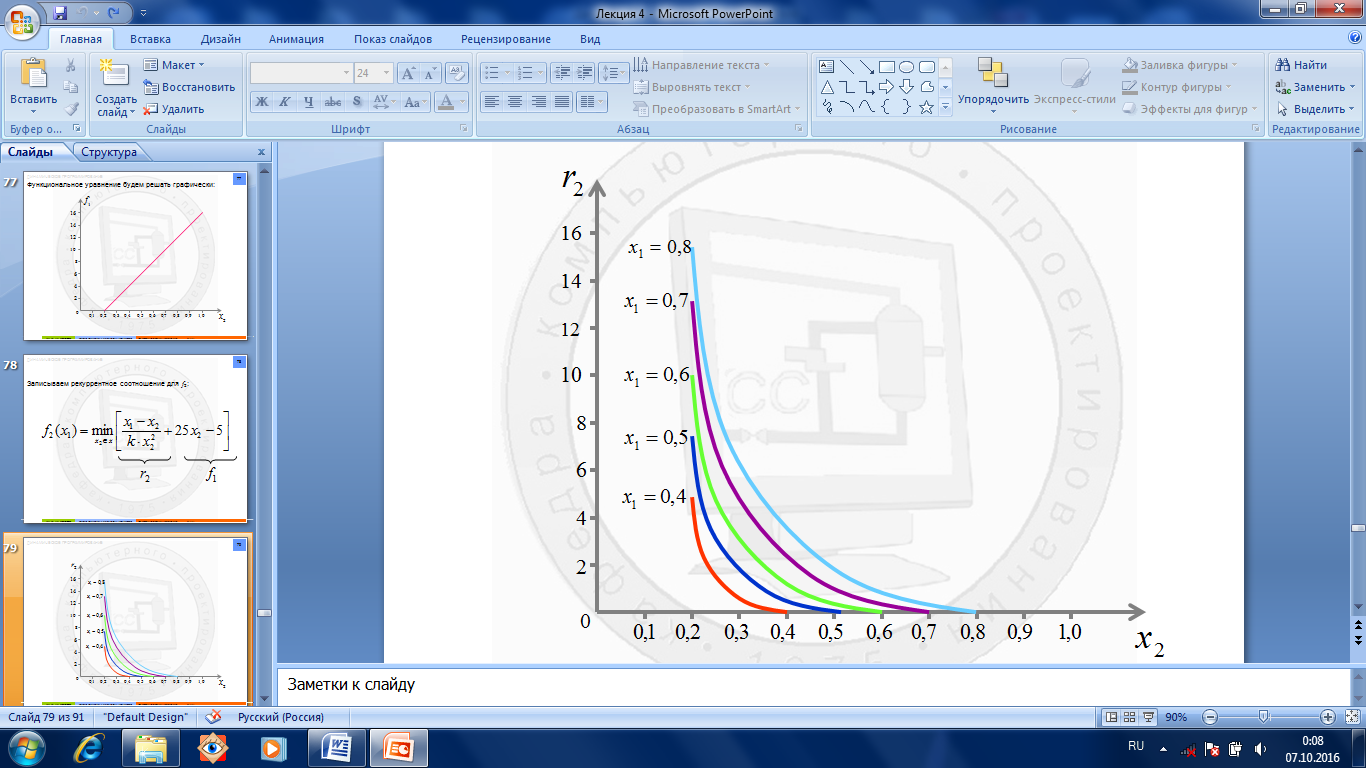
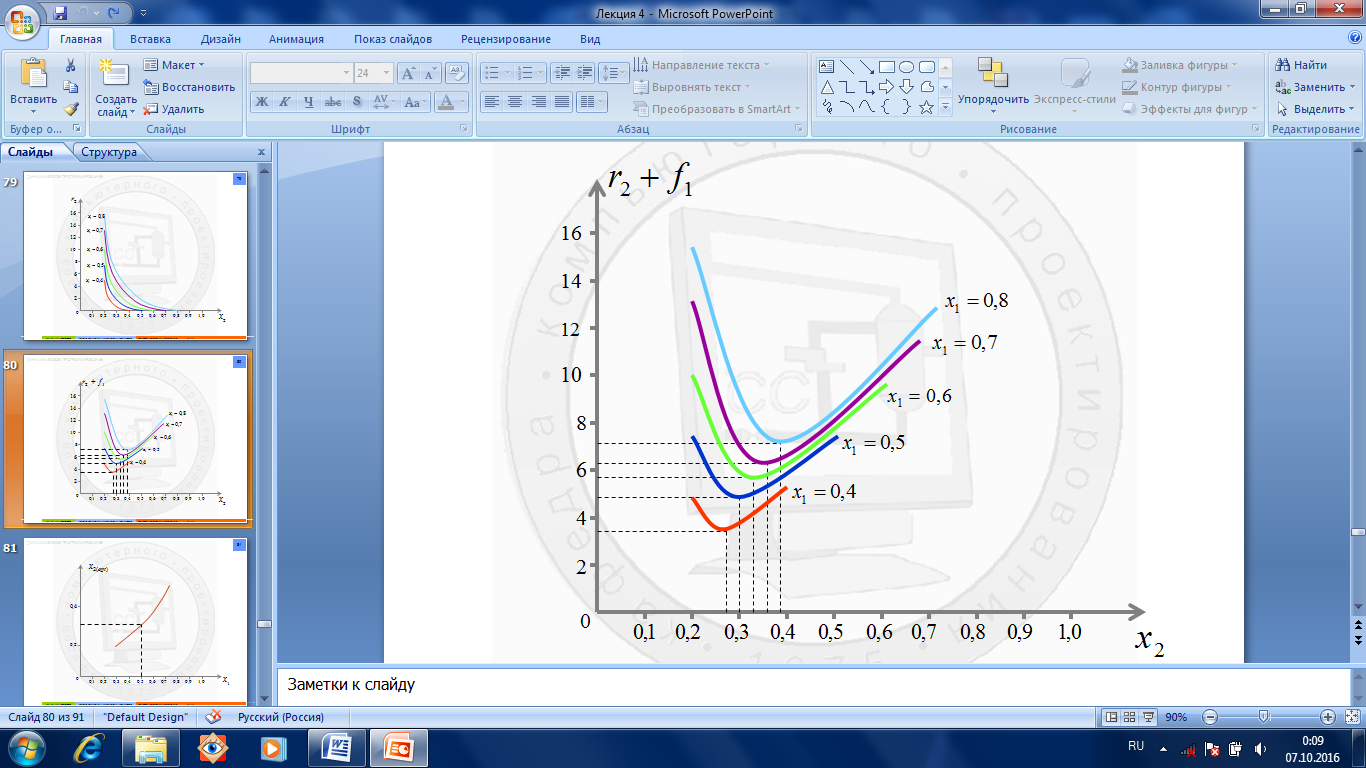

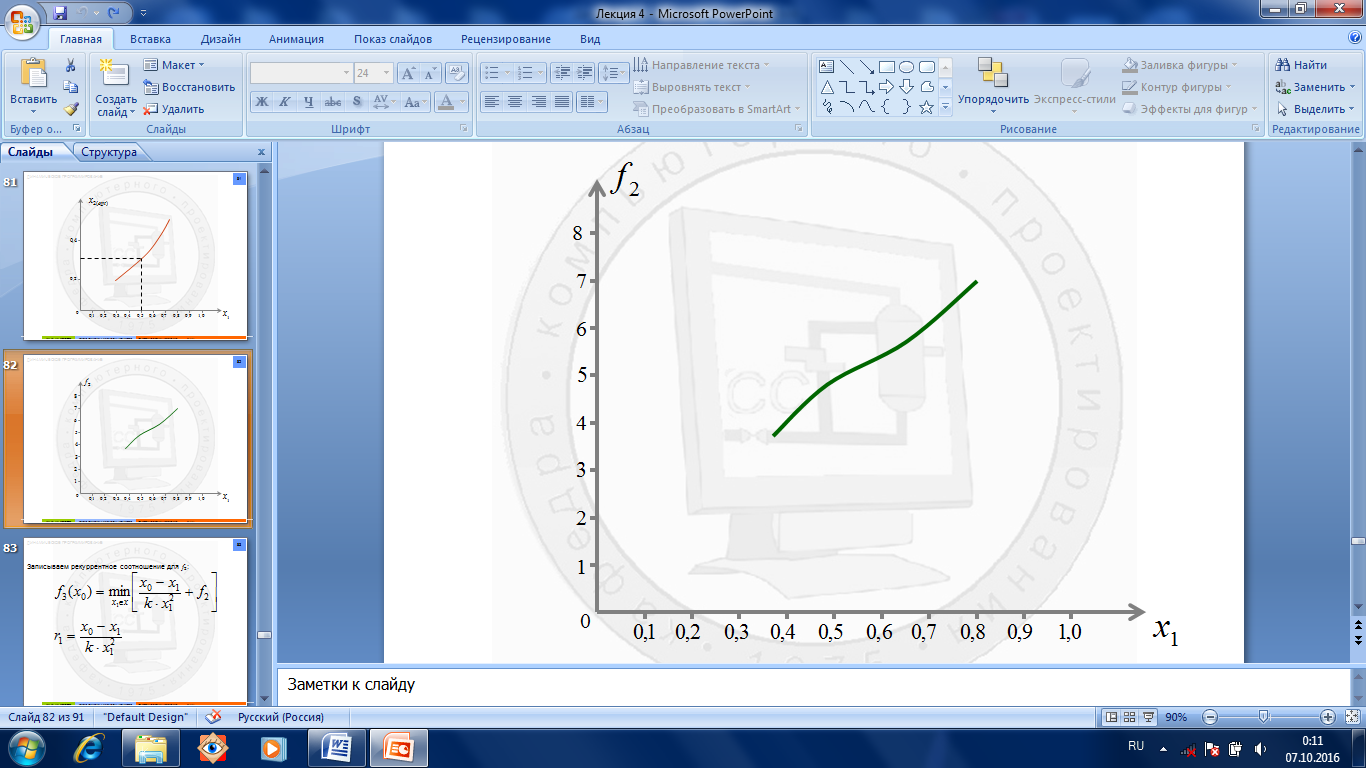
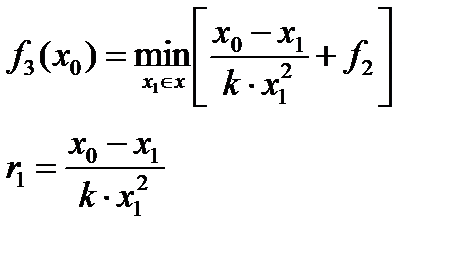 Рис.1.7.6. Рекуррентное соотношение
Рис.1.7.6. Рекуррентное соотношение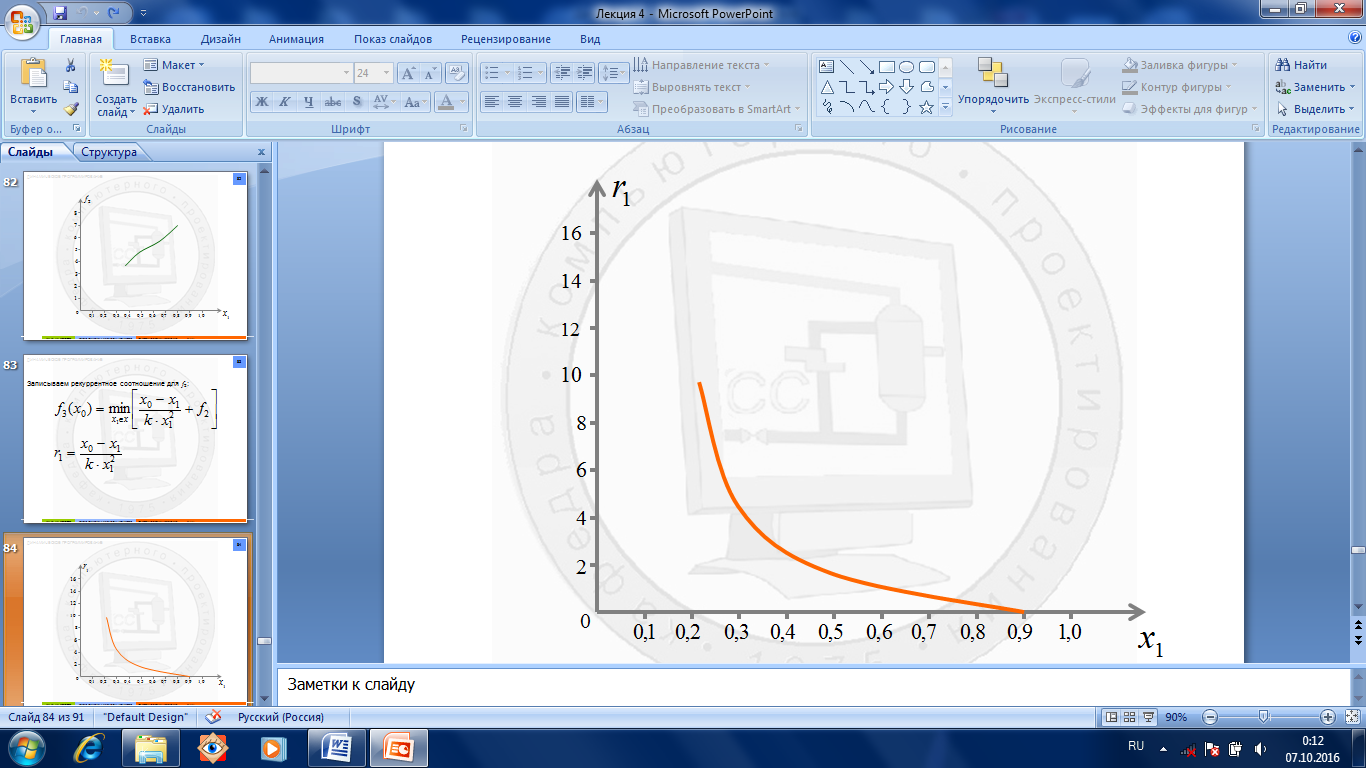
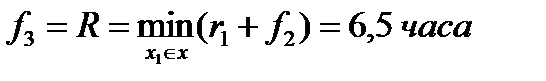 Второй этап решения
Второй этап решения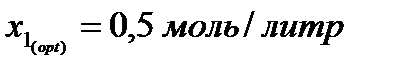 Из графических построений определяется:
Из графических построений определяется: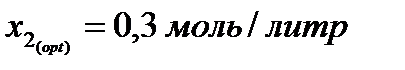 По найденному значению x 1( opt )
По найденному значению x 1( opt )