
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывность функции в точке ⇐ ПредыдущаяСтр 3 из 3
Пусть функция Определение 4.1. Функция Таким образом, функция 1. функция определена в некоторой окрестности точки а, т.е. существует 2.
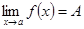 ; ;
3.

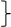   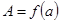 . .
Рис. 7 Обозначим
Таким образом, непрерывность функции в точке означает, что бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции. Определение 4.2. Если функция Аналогично, если функция Например, функция
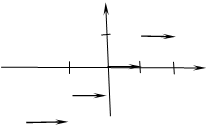
Рис.8 Очевидно, что функция непрерывна в данной точке тогда и только тогда, когда она непрерывна как справа, так и слева в этой точке. Точки разрыва Пусть функция Определение 4.3. Точка а называется точкой разрыва функции Следовательно, а – точка разрыва функции 1. 2. 3. Определение 4.4. Точка а называется точкой разрыва первого рода функции 1. если
2. если
В этом случае говорят, что функция доопределена по непрерывности в точке а. Определение 4.5. Точка а называется точкой разрыва второго рода функции
 непрерывности. непрерывности.
1.
 
 ; ;  – точка устранимого разрыва первого рода, (рис.10). – точка устранимого разрыва первого рода, (рис.10).
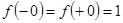    . Доопределим эту функцию по непрерывности, . Доопределим эту функцию по непрерывности,
Рис. 10
 получим функцию получим функцию 
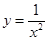 ; ;  – точка разрыва второго рода, (рис.11) т.к. – точка разрыва второго рода, (рис.11) т.к.
Свойства функций, непрерывных в точке Если функции
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 60; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.197.35 (0.015 с.) |
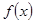 определена в некоторой окрестности точки а.
определена в некоторой окрестности точки а.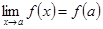 . (*)
. (*)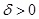 такое, что
такое, что 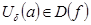 ;
;
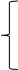
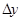

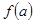


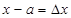 – приращение аргумента,
– приращение аргумента, 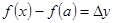 – приращение функции, соответствующее этому приращению аргумента, тогда, если
– приращение функции, соответствующее этому приращению аргумента, тогда, если 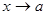 , то
, то  и
и 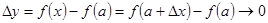 . Тогда равенство (*) примет вид:
. Тогда равенство (*) примет вид: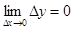 .
.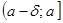 и
и 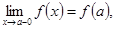 т.е.
т.е. 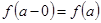 , то эту функцию называют непрерывной слева в точке а.
, то эту функцию называют непрерывной слева в точке а.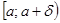 и
и 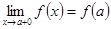 , т.е.
, т.е. 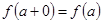 , то эту функцию называют непрерывной справа в точке а.
, то эту функцию называют непрерывной справа в точке а.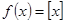 – (целая часть x, рис.8) непрерывна в точке
– (целая часть x, рис.8) непрерывна в точке 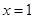 справа и не является непрерывной в этой точке слева, т.к.
справа и не является непрерывной в этой точке слева, т.к. 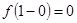 ,
, 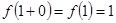 , или
, или  ,
,  .
.
 ;
;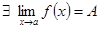 ;
;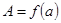 .
. , если в этой точке существуют конечные пределы слева и справа (односторонние пределы), т.е.
, если в этой точке существуют конечные пределы слева и справа (односторонние пределы), т.е. 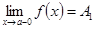 ,
,  . При этом:
. При этом: , то а – точка неустранимого разрыва, величина
, то а – точка неустранимого разрыва, величина  называется скачком функции в точке разрыва первого рода;
называется скачком функции в точке разрыва первого рода; , то а – точка устранимого разрыва. Полагая
, то а – точка устранимого разрыва. Полагая 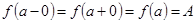 , получим функцию, непрерывную в точке а и совпадающую с
, получим функцию, непрерывную в точке а и совпадающую с  :
:
 характер, в случае устранимого разрыва доопределить функцию по
характер, в случае устранимого разрыва доопределить функцию по
 ;
; 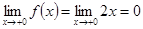 ;
; – точка разрыва первого рода (скачок), (рис.9). Рис.9
– точка разрыва первого рода (скачок), (рис.9). Рис.9 

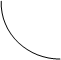

 . Рис.11
. Рис.11 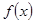 и
и 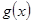 непрерывны в точке а, то функции
непрерывны в точке а, то функции 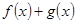 ,
,  ,
, 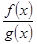
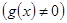 непрерывны в точке а.
непрерывны в точке а.


