
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ЛЕКЦИЯ 2. Производные высших порядков ⇐ ПредыдущаяСтр 3 из 3
Производная
Если этот предел существует и конечен, то он называется второй производной от функции f (x) в точке х. Принятое обозначение:
По-другому ещё называют производная второго порядка. Подобным образом вводят производные n -го порядка f (n)(x) = (f (n-1)(x))¢. В механике вторая производная от пути по времени есть ускорение Доказательство. Если материальная точка М движется прямолинейно по закону Отношение Но Пример. Производные от степенной функции y = х n. y ¢ = n x n-1, y ¢¢ = n (n-1) x n-2, y ¢¢¢ = n (n-1) (n-2) x n-3, ..., y(k) = n (n-1) (n-2)...(n-k+1) x (n-k) при (к £ n). Производные высших порядков можно найти и для неявно заданных функций, а также для функций, заданных параметрически (как и производные первого порядка). Дифференциалом второго порядка называется дифференциал от первого дифференциала d(d f (x)) = (d f (x))¢Dx = (f ¢(x)D x)¢D x = f ¢¢(x) (D x)2.
Применение дифференциала к приближенным вычислениям: равенство
Теоремы о дифференцируемых функциях. Для дифференцируемых функций выполняется ряд важных для приложений теорем. Перечислим основные теоремы. Теорема Ролля Пусть функция у = f (x): 1. непрерывна на отрезке [a, b], 2. дифференцируема во всех внутренних точках отрезка, т. е. в интервале (a,b), 3. f (а) = f (b). Тогда внутри отрезка (a, b) существует по крайней мере одна точка Замечание. Точка с является корнем производной. Если f(а) = f(b) =0, то теорема формулируется так: между корнями функции лежит корень производной.
Формула Лагранжа (формула конечных приращений). Пусть функция у = f (x) непрерывна на отрезке [a,b], дифференцируема во всех внутренних точках отрезка, т. е. в интервале (a,b), то внутри отрезка существует по крайней мере одна точка с a < c < b в которой справедливо равенство: полное приращение функции равно производной, вычисленной в точке с, умноженной на длину промежутка f (b) - f (а) = f `(c)(b - а). (7.18)
В точке с касательная параллельна секущей MN (см. рис. 7.4).
Рис. 2.1. Геометрический смысл формулы конечных приращений.
Правило Лопиталя. Пусть функции f (x) и g (x) на отрезке [a,b] удовлетворяют условию теоремы Коши и f (с) = g (с) = 0 (a < c < b), то, если существует предел отношения производных при х →с, то существует и предел отношения функций в этой точке, причем
Замечание. Правило Лопиталя можно применять и для раскрытия неопределенностей типа Коротко полученную формулу читают так: предел отношения двух бесконечно малых равен пределу отношения их производных, если последний существует. Если производные
Пример. Вычислить предел Решение. Так как е-х = 1/ех, то предел можно преобразовать к виду
ЛЕКЦИЯ 3. Приложение производных к исследованию функций. Использование производных позволяет прояснить многие особенности в поведении функций. Наиболее важными особенностями функций являются интервалы монотонности и точки экстремумов функций. Если функция относится к классу дифференцируемых монотонных функций, то ее производная сохраняет знак на интервале монотонности, причем возрастающая функция имеет положительную производную, а убывающая – отрицательную. Действительно, если Δх > 0, то так как
то знак производной совпадает со знаком приращения функции.
Для возрастающих функций
Δf(x) > 0
для убывающих функций
Δf(x) < 0 Необходимые условия возрастания и убывания функций: если дифференцируемая на интервале Достаточные условия: если функция Функция имеет локальный максимум (минимум) в точке х 0, если она определена как в точке х 0, так и в окрестности этой точки, и значение функции в точке х 0 больше (меньше), чем ее значения во всех соседних точках: т. е.
f (х 0) > f (x) в точках максимума
f (х 0) < f (x) в точках минимума
для всех х из окрестности точки х 0.
Минимумы и максимумы функции объединены единым понятием – экстремумы. До точки максимума функция возрастает, следовательно, ее производная положительна
f `(x) > 0
после точки максимума – убывает, производная отрицательна
f `(x) < 0.
Для точки минимума первоначально функция убывает
f `(x) < 0,
а потом возрастает
f `(x)>0).
В самих точках экстремумов производная или равна нулю (обычный экстремум) или не существует (острый экстремум). На рис. 3.1 функция имеет экстремумы в точках х1, х2 и х3, причем в точке х1 – острый максимум, а в точках х2 и х3 обычный минимум и максимум. Тем самым, в точках экстремумов функции производная равна нулю или не существует (необходимое условие экстремума) и меняет знак с «+» на «-» в точках максимумов и с «-» на «+» в точках минимумов (достаточные условия экстремума).
Рис. 3.1. Экстремумы функции Точки, в которых производная равна нулю, называются стационарными точками. Не все стационарные точки являются точками экстремумов. В стационарных точках надо проверять достаточное условие экстремума. Замечание. Не надо путать наибольшее и наименьшее значение и экстремумы. Экстремум достигается всегда внутри промежутка, а наибольшее и наименьшее значения могут достигаться и в точках экстремумов, и на границах промежутка, и в точках разрыва. На рис. 3.1 точка х3 является точкой максимума и в ней также достигается наибольшее значение, наименьшее значение достигается в точке а, т.е. на границе промежутка.
Функция называется выпуклой (выпуклость вверх) на интервале (a,b), если график функции лежит под любой касательной в каждой точке интервала, на всем интервале выпуклости вторая производная отрицательна f ``(x) < 0. Функция называется вогнутой (выпуклость вниз) на интервале (a,b), если график функции лежит над любой касательной в каждой точке интервала, на всем интервале вогнутости вторая производная положительна f ``(x) > 0. Следовательно, в точках экстремумов вторая производная имеет определенный знак (достаточное условие экстремума по второй производной): в точках максимумов f ``(x 0) < 0, в точках минимумов f ``(x0) > 0. Достаточное условие существования точек перегиба. Если вторая производная
Рис. 3.2. Выпуклость и вогнутость кривой. Точка перегиба. Пример: y = x 2 e- x y `= 0 если x = 0 или x = 2, это стационарные точки.
y ``= (2 x e- x – x 2e- x ))’ = 2e-x - 2 x e-x – 2 x e-x + x 2 e-x = e-x(2 - 4 x + x 2); y``= 0 если x1,2 =2 это точки перегиба y``(0) = 2 > 0, следовательно, в точке х = 0 минимум, y``(2) = -2e-2 < 0, следовательно в точке х = 2 максимум.
Асимптоты графика функции. Построение графика функции значительно облегчается, если знать его асимптоты. Понятие асимптоты рассматривалось при изучении формы гиперболы (в теме «кривые второго порядка»). Определение: асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой (рис. 3.3).
Асимптоты могут быть вертикальными, наклонными и горизонтальными. Горизонтальная асимптота – это частный случай наклонной асимптоты. Прямая Действительно, в этом случае непосредственно из рисунка 3.3 видно, что расстояние точки
Прямая y = kx + b называется наклонной асимптотой для функции f (x), если при х→∞ расстояние от переменной точки графика функции М до прямой стремится к нулю (рис. 3.4). При этом
Рис. 3.4. Наклонная асимптота Если хотя бы один из пределов k и b не существует или равен бесконечности, то кривая В частности, если Замечание: Асимптоты графика функции Пример. y = x e-x.
Прямая у = 0 является горизонтальной асимптотой.
|
|||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 561; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.87.95 (0.042 с.) |
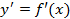 является функцией того же аргумента х, что и исходная функция. Поэтому ее можно опять дифференцировать, т.е. вычислять предел отношения приращения производной к приращению аргумента
является функцией того же аргумента х, что и исходная функция. Поэтому ее можно опять дифференцировать, т.е. вычислять предел отношения приращения производной к приращению аргумента =
= 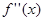 .
.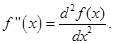
 .
.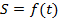 , производная
, производная  равна скорости точки в данный момент времени:
равна скорости точки в данный момент времени:  . Пусть в момент времени t скорость точки равна V, а в момент
. Пусть в момент времени t скорость точки равна V, а в момент 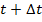 – скорость равна
– скорость равна 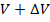 , т.е. за промежуток времени
, т.е. за промежуток времени 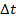 скорость изменилась на величину
скорость изменилась на величину  .
. выражает среднее ускорение движения точки за время
выражает среднее ускорение движения точки за время 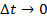 называется ускорением точки М в данный момент t и обозначается буквой a:
называется ускорением точки М в данный момент t и обозначается буквой a: 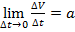 , т.е.
, т.е.  .
. . Поэтому
. Поэтому 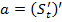 , т.е.
, т.е.  .
.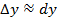 позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции. Дифференциал обычно находится значительно проще, чем приращение функции, поэтому равенство выше широко применяется в вычислительной практике.
позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции. Дифференциал обычно находится значительно проще, чем приращение функции, поэтому равенство выше широко применяется в вычислительной практике.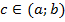 , в которой производная обращается в ноль – f `(c) = 0.
, в которой производная обращается в ноль – f `(c) = 0.



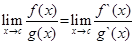 (2.1)
(2.1) .
.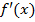 и
и 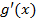 удовлетворяют тем же условиям, что и функции
удовлетворяют тем же условиям, что и функции 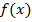 и
и 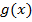 , теорему (2.1) можно применить ещё раз:
, теорему (2.1) можно применить ещё раз: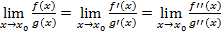 . (2.2)
. (2.2)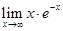 .
.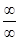
 .
.



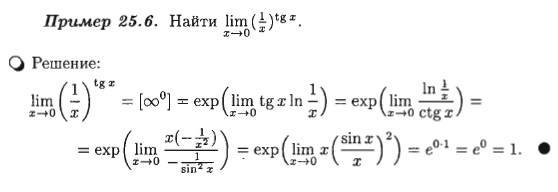
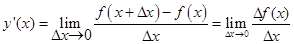
 f `(x) > 0,
f `(x) > 0, функция
функция  возрастает (убывает), то
возрастает (убывает), то  .
. и
и , то эта функция возрастает (убывает) на интервале
, то эта функция возрастает (убывает) на интервале 
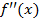 при переходе через точку
при переходе через точку 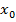 , в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой
, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой 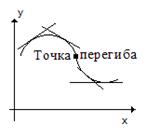
 y `= 2 x e- x - x 2 e- x = x e- x (2 – x);
y `= 2 x e- x - x 2 e- x = x e- x (2 – x);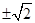 ,
,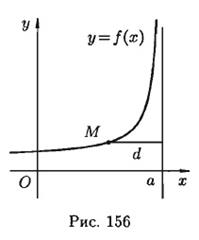 Рис. 3.3.
Рис. 3.3.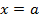 является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции 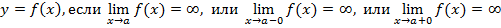 .
.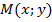 кривой от прямой
кривой от прямой 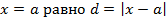 . Если
. Если 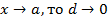 . Согласно определению асимптоты, прямая
. Согласно определению асимптоты, прямая 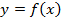 . Для отыскания вертикальных асимптот нужно найти те значения x, вблизи которых функция
. Для отыскания вертикальных асимптот нужно найти те значения x, вблизи которых функция 

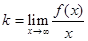 ,
, 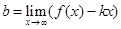 .
.
 . Поэтому
. Поэтому 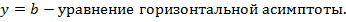
 могут быть разными. Поэтому при нахождении пределов k и b следует отдельно рассматривать случай, когда
могут быть разными. Поэтому при нахождении пределов k и b следует отдельно рассматривать случай, когда 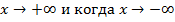 .
.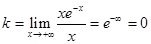 ,
,  .
.


