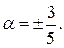Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. Прямоугольный декартов базис. ⇐ ПредыдущаяСтр 2 из 2
Разложение вектора в декартовом базисе
Рассмотрим пространство 0 xyz, т.е. введем в пространстве прямоугольную декартовую систему координат. Векторы
Теорема. Любой вектор
Такое представление вектора Проекции называются прямоугольными декартовыми координатами вектора
II. Операции над векторами, заданными их разложениями по ортам (заданными координатами) Пусть даны два вектора Тогда сумма векторов:
Разность векторов:
Произведение вектора на число
Итак,
Пример 5.1.
III. Модуль вектора
По теореме о длине диагонали параллелепипеда
IV. Расстояние между двумя точками в пространстве
Рассмотрим вектор
Тогда Расстояние между точками А и В равно
Частный случай. Расстояние между точками на плоскости
V. Направляющие косинусы
Направление вектора в пространстве определяется углами По свойству 1 проекций:
или Тогда
VI. Условие коллинеарности двух векторов
Для того, чтобы два вектора
Скалярное произведение векторов I. Определение Опр. Скалярным произведением векторов
Придадим (3.5) другой вид (по свойству 1 проекций).
II. Свойства скалярного произведения 1. Переместительное свойство Доказательство из определения. 2. Сочетательное свойство относительно скалярного множителя 3. Распределительное свойство Пример 6.1. Векторы Условие ортогональности векторов По определению
Итак, для того, чтобы два ненулевых вектора были ортогональны, необходимо и достаточно, чтобы их скалярное произведение равнялось нулю.
Пример 6.2. При каком
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.145.114 (0.011 с.) |

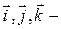 единичные векторы осей О x, Oy, Oz. Векторы
единичные векторы осей О x, Oy, Oz. Векторы 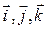 называются ортами. Поскольку
называются ортами. Поскольку 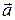 , заданный в пространстве 0 xyz, может быть представлен в виде
, заданный в пространстве 0 xyz, может быть представлен в виде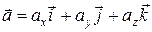 . (3.4)
. (3.4)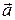 называется разложением вектора в декартовом базисе или разложением вектора по ортам.
называется разложением вектора в декартовом базисе или разложением вектора по ортам.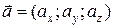 или
или 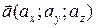 . Каждый вектор имеет единственное представление в виде (3.4) в заданном базисе.
. Каждый вектор имеет единственное представление в виде (3.4) в заданном базисе.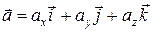 и
и  .
.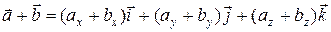 .
.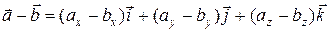 .
.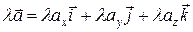 .
.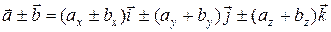 ,
,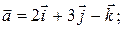
 . Найти
. Найти 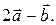
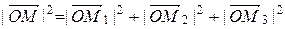 или
или 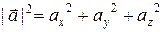 .
.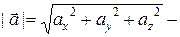 модуль вектора
модуль вектора  , где
, где 
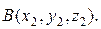
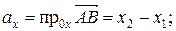
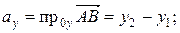

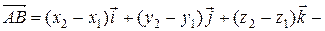 разложение
разложение 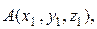
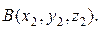
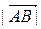 .значит
.значит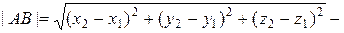 расстояние между точками
расстояние между точками 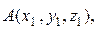
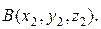
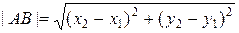 , где
, где 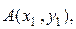
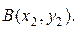
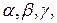 которые вектор составляет с осями Ox, Oy, Oz. Косинусы этих углов, т.е.
которые вектор составляет с осями Ox, Oy, Oz. Косинусы этих углов, т.е. 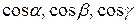 называются направляющими косинусами вектора.
называются направляющими косинусами вектора.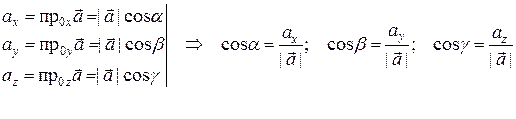

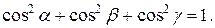
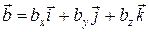 были коллинеарны, необходимо и достаточно, чтобы их проекции были пропорциональны
были коллинеарны, необходимо и достаточно, чтобы их проекции были пропорциональны условие коллинераности векторов.
условие коллинераности векторов.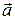 и
и 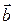 называется число, равное произведению модулей этих векторов на косинус угла между ними.
называется число, равное произведению модулей этих векторов на косинус угла между ними.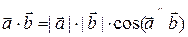 . (3.5)
. (3.5) проекция
проекция  на ось, определяемую
на ось, определяемую 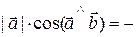 проекция
проекция 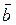 .
. (3.6)
(3.6)
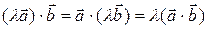 .
.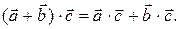
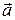 и
и 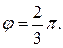 Зная, что
Зная, что 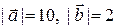 вычислить
вычислить 
 .
. 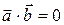 , если
, если 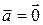 или
или 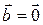 , или
, или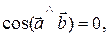 т.е.
т.е.  Пусть
Пусть 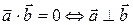 .
.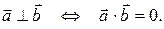
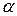 векторы
векторы 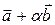 и
и 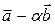 ортогональны, если
ортогональны, если 
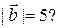 Ответ:
Ответ: