
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные операции над векторами.Стр 1 из 2Следующая ⇒
II. Векторная алгебра Лекция № 6. Понятие вектора. Проекции вектора. Определение: Вектор – это направленный отрезок прямой. Вектор обозначается обычно двумя буквами, сначала пишется буква, указывающая начало, а потом, буква, указывающая конец вектора. Вектор обозначается
Рис. 1
Определение: Длина вектора называется его модулем и обозначается символом Определение: Вектор, длина которого равна нулю, называется нулевым вектором. Нулевой вектор направления не имеет. Обозначается Определение: Вектор, длина которого равна единице, называется единичным вектором и обозначается Определение: Векторы, расположенные на одной прямой или параллельных прямых, называются коллинеарными. (Рис. 3)
Рис. 2 Определение: Два вектора называются равными, если они: 1. имеют равные модули 2. коллинеарны 3. направлены в одну сторону (Рис. 3)
Рис. 3
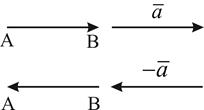
Определение: Вектора называются противоположными, если они: 1. имеют равные модули 2. коллинеарны 3. направлены в противоположную сторону(Рис. 4)
Рис. 4
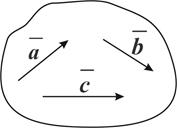
Определение: Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или параллельны некоторой плоскости. (Рис. 5)
Рис. 5 Определение: Проекцией вектора Проекция вектора на ось положительна, если вектор образует с осью острый угол и отрицательна, если вектор образует с осью тупой угол. (Рис. 6)
Рис. 6
Проекции вектора на координатные оси называют также его (декартовыми) координатами. Координаты вектора равны разностям соответствующих координат его конца и начала. Если для вектора
Модуль вектора равен арифметическому значению квадратного корня из суммы квадратов его проекций. Модуль вектора через его проекции на оси прямоугольной системы координат вычисляется по формуле:
Если вектор Определение: Радиус – вектор точки
Рис. 7 Если a, b, g - углы, образованные вектором Сумма квадратов направляющих косинусов ненулевого вектора равна единице Координатами единичного вектора Задачи Задача 1. Вектор Решение: Проекции вектора
Длина вектора Направляющие косинусы: Задача 2. Дан модуль вектора Решение: Используем формулу (9) для определения
Так как g - тупой угол, следовательно,
Замечание. Т. к. вектор При умножении вектора Задачи Задача 1. Найти сумму и разность векторов Решение: По формуле имеем
Задача 2. Проверить коллинеарность векторов Решение: По формулам находим векторы
Вектор Замечание. Если Замечание. Если даны углы a, b, g, которые ось u составляет с координатными осями, то
Рис. 2 Если вектор
Рис. 3 Работа силы: Задачи Задача 1. Найти скалярное произведение векторов Решение: Имеем
Задача 2. Даны точки Вычислить Решение: Найдем координаты векторов
По формуле (10) найдем
Задача 3. Вычислить угол, образованный векторами Решение: По формуле
Задача 4. Даны векторы Решение: Используя формулу (13), получаем
Задача 5. Дан вектор Решение: Т. к. ось u составляет с координатными осями равные острые углы, т. е. Но
Лекция №8. Векторное произведение двух векторов. Смешанное произведение трех векторов. Задачи Задача 1. Раскрыть скобки и упростить выражение Решение: Используя свойства векторного произведения (формулы 4, 5), получаем т. к. Задача 2. Найти площадь параллелограмма, построенного на векторах Решение:
Задача 3. Найти векторное произведение векторов Решение: По формуле (7) имеем
Задача 4. Найти площадь треугольника, координаты вершин которого известны: Решение:
Найдем проекции векторов
По формулам (7) для векторного произведения векторов найдем, что
Объем треугольной пирамиды
Замечание1. Знак перед определителем должен быть выбран так, чтобы объем V был положительным. Замечание 2. Предполагается, что векторы Задачи. Задача 1. Вектор Решение:
Рис. 1 Рис. 2 По условию задачи тройка векторов
По условию задачи Угол Задача 2. Даны координаты вершин пирамиды Решение:
В правой части выбран знак минус, так как определитель отрицателен. Задача 4. Показать, что точки Решение:
Находим смешанное произведение векторов:
Поскольку
II. Векторная алгебра Лекция № 6. Понятие вектора. Проекции вектора. Определение: Вектор – это направленный отрезок прямой. Вектор обозначается обычно двумя буквами, сначала пишется буква, указывающая начало, а потом, буква, указывающая конец вектора. Вектор обозначается
Рис. 1
Определение: Длина вектора называется его модулем и обозначается символом Определение: Вектор, длина которого равна нулю, называется нулевым вектором. Нулевой вектор направления не имеет. Обозначается Определение: Вектор, длина которого равна единице, называется единичным вектором и обозначается Определение: Векторы, расположенные на одной прямой или параллельных прямых, называются коллинеарными. (Рис. 3)
Рис. 2 Определение: Два вектора называются равными, если они: 1. имеют равные модули 2. коллинеарны 3. направлены в одну сторону (Рис. 3)
Рис. 3
Определение: Вектора называются противоположными, если они: 1. имеют равные модули 2. коллинеарны 3. направлены в противоположную сторону(Рис. 4)
Рис. 4
Определение: Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или параллельны некоторой плоскости. (Рис. 5)
Рис. 5 Определение: Проекцией вектора Проекция вектора на ось положительна, если вектор образует с осью острый угол и отрицательна, если вектор образует с осью тупой угол. (Рис. 6)
Рис. 6
Проекции вектора на координатные оси называют также его (декартовыми) координатами. Координаты вектора равны разностям соответствующих координат его конца и начала. Если для вектора
Модуль вектора равен арифметическому значению квадратного корня из суммы квадратов его проекций. Модуль вектора через его проекции на оси прямоугольной системы координат вычисляется по формуле:
Если вектор
Определение: Радиус – вектор точки
Рис. 7 Если a, b, g - углы, образованные вектором Сумма квадратов направляющих косинусов ненулевого вектора равна единице Координатами единичного вектора Задачи Задача 1. Вектор Решение: Проекции вектора
Длина вектора Направляющие косинусы: Задача 2. Дан модуль вектора Решение: Используем формулу (9) для определения
Так как g - тупой угол, следовательно,
Линейные операции над векторами. Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число. Пусть
Рис. 1 Это правило сложения векторов называют правилом треугольника. Сумму двух векторов можно построить также по правилу параллелограмма. Отложим от точки О векторы
Рис. 2 Модуль вектора
Разностью двух векторов
Если на векторах
Рис. 4 Модуль вектора При умножении вектора Полученный вектор 1. 2. вектор 3. 4. Замечание. Т. к. вектор При умножении вектора
|
||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 73; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.150.119 (0.148 с.) |
 или
или 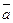 .
.
 или
или 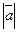 .
. - нулевой вектор.
- нулевой вектор. - единичный вектор
- единичный вектор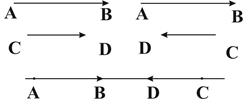

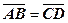 или
или 
 и
и 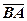 - противоположные векторы или
- противоположные векторы или  и
и 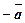
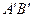 , заключенного между проекциями начала и конца вектора на эту ось. Эта длина берется со знаком плюс, если направление отрезка
, заключенного между проекциями начала и конца вектора на эту ось. Эта длина берется со знаком плюс, если направление отрезка 
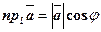
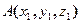 и координаты его конца
и координаты его конца 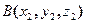 , то проекции вектора
, то проекции вектора 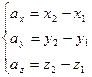
 б
б
 исходит из начала координат, а его конец М имеет координаты
исходит из начала координат, а его конец М имеет координаты 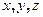 , то тогда его проекции на координатные оси равны координатам его конца:
, то тогда его проекции на координатные оси равны координатам его конца: 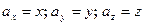 .
.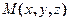 обозначается через
обозначается через 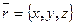 . Модуль радиус - вектора точки
. Модуль радиус - вектора точки 
 - называют направляющими косинусами вектора
- называют направляющими косинусами вектора 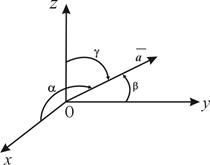

 . Данное равенство позволяет определить один из углов a, b, g, если известны два других.
. Данное равенство позволяет определить один из углов a, b, g, если известны два других.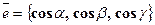
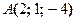 ;
; 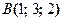 . Найти проекции вектора
. Найти проекции вектора  ,
,  ,
, 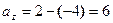 .
. .
.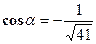 ;
; 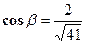 ;
;  .
. и его углы с осями координат:
и его углы с осями координат: 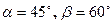 , а g - тупой угол. Вычислить проекции этого вектора на координатной оси.
, а g - тупой угол. Вычислить проекции этого вектора на координатной оси.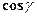 .
.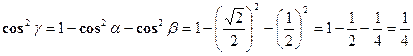

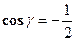 . Проекции вектора
. Проекции вектора 
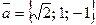 .
. коллинеарен вектору
коллинеарен вектору  , то в дальнейшем условие коллинеарности векторов будем записывать в виде
, то в дальнейшем условие коллинеарности векторов будем записывать в виде 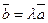 .
.
 .
. или
или 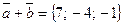
 или
или  .
.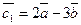 и
и 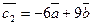 , где
, где  ,
,  . Установить, какой из них длиннее другого, во сколько раз, как они направлены: в одну или противоположные стороны.
. Установить, какой из них длиннее другого, во сколько раз, как они направлены: в одну или противоположные стороны.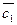 и
и  в координатной форме.
в координатной форме. ,
, 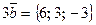 ,
, 
 ,
,  ,
, 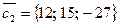
 , т. к.
, т. к. 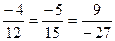 ,
,  .
. ), т. к.
), т. к. 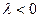 .
.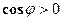 , угол j - острый,
, угол j - острый, , угол j - тупой.
, угол j - тупой.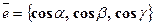 и для вычисления проекции вектора
и для вычисления проекции вектора 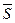 на ось u служит формула:
на ось u служит формула: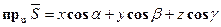
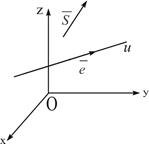
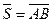 изображает перемещение материальной точки под действием постоянной силы
изображает перемещение материальной точки под действием постоянной силы 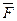 (Рис. 3), то работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению вектора силы на вектор перемещения.
(Рис. 3), то работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению вектора силы на вектор перемещения.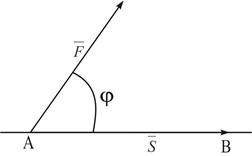
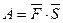 .
.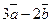 и
и 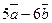 , если
, если 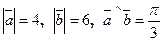 .
.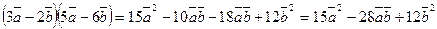 (используем свойства скалярного произведения – формулы (5), (6), (7)). По формулам (2) и (9), получаем
(используем свойства скалярного произведения – формулы (5), (6), (7)). По формулам (2) и (9), получаем 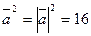 ,
, 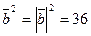 ,
, 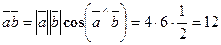
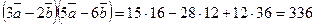
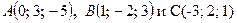 .
.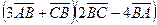 .
.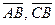 .
.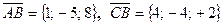 .
.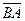 - противоположен вектору
- противоположен вектору 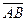 , следовательно,
, следовательно, 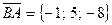 . Аналогично
. Аналогично 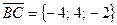 .
.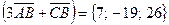 ;
; 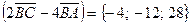 .
.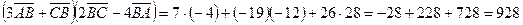 .
.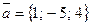 и
и 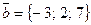 .
.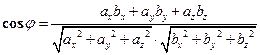 , получаем
, получаем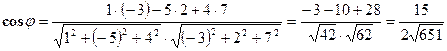
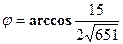
 и
и 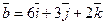 . Найти
. Найти 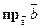 и
и 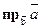 .
.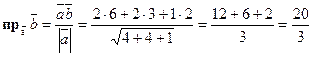
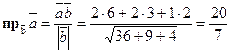
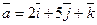 . Найти его проекцию на ось u, составляющую с координатными осями равные острые углы.
. Найти его проекцию на ось u, составляющую с координатными осями равные острые углы.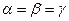 , то
, то 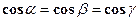 .
.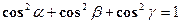 , и т. к. в этой сумме все слагаемые между собой равны, то
, и т. к. в этой сумме все слагаемые между собой равны, то 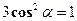 ;
; 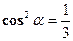 ;
; 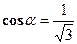 , тогда
, тогда 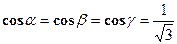 (знак плюс перед корнем взят потому, что по условию углы a, b, g - острые, значит косинусы их положительны). Т. к. по условию
(знак плюс перед корнем взят потому, что по условию углы a, b, g - острые, значит косинусы их положительны). Т. к. по условию 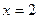 ,
, 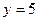 ,
,  , то по формуле получаем
, то по формуле получаем 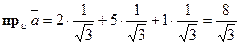 .
.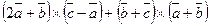 .
.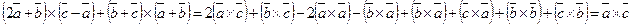 ,
, ,
, 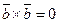 ,
, 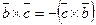 ,
,  .
.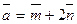 и
и  , где
, где 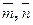 - единичные векторы, образующие угол
- единичные векторы, образующие угол 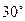 .
.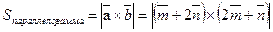
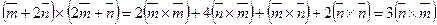 , т. к.
, т. к. 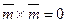 ,
,  ,
, 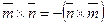


 и
и 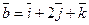 .
.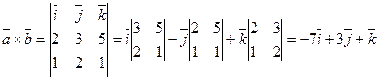

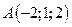 ,
,  ,
, 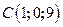 .
. Рассмотрим векторы
Рассмотрим векторы  . Площадь треугольника ABC есть половина площади параллелограмма, построенного на векторах
. Площадь треугольника ABC есть половина площади параллелограмма, построенного на векторах 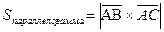 ,
,  .
.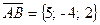 ,
, 
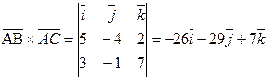


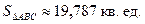
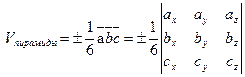 .
.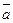 ,
, 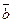 и
и 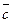 не лежат в одной плоскости (некомпланарны).
не лежат в одной плоскости (некомпланарны). и
и  равен
равен 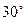 . Зная, что
. Зная, что 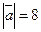 ,
, 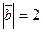 ,
, 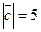 , вычислить
, вычислить 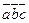 .
.
 , где
, где  ,
, 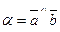 .
. .
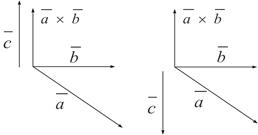
.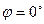 (Рис. 1),
(Рис. 1), 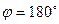 (Рис. 2), следовательно,
(Рис. 2), следовательно,  . Тогда
. Тогда 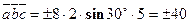 .
. ,
, 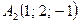 ,
, 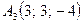 и
и  . Определить ее объем.
. Определить ее объем. Рис. 3
Рис. 3
 ,
,  ,
, 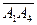 .
.


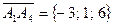 Найдем объем пирамиды по формуле (9)
Найдем объем пирамиды по формуле (9)


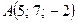 ,
,  ,
, 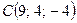 и
и  лежат в одной плоскости.
лежат в одной плоскости.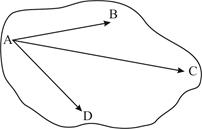 Рассмотрим три вектора
Рассмотрим три вектора 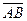 ,
,  .
.

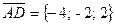
 (Элементы первого и третьего столбцов пропорциональны).
(Элементы первого и третьего столбцов пропорциональны).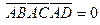 , то векторы компланарны, т. е. точки A, B, C, D лежат в одной плоскости.
, то векторы компланарны, т. е. точки A, B, C, D лежат в одной плоскости. и
и 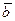 - два произвольных вектора. Возьмем произвольную точку О и построим вектор
- два произвольных вектора. Возьмем произвольную точку О и построим вектор 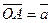 ; затем от точки А отложим вектор
; затем от точки А отложим вектор 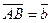 . Вектор
. Вектор 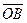 , соединяющий начало первого слагаемого вектора с концом второго называется суммой этих векторов
, соединяющий начало первого слагаемого вектора с концом второго называется суммой этих векторов  . (Рис. 1)
. (Рис. 1)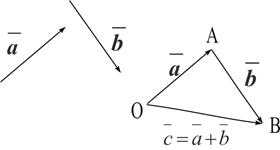
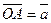 и
и  . Построим на этих векторах как на сторонах параллелограмм OACB. Вектор
. Построим на этих векторах как на сторонах параллелограмм OACB. Вектор  , служащий диагональю параллелограмма, проведенной из вершины О, является суммой векторов
, служащий диагональю параллелограмма, проведенной из вершины О, является суммой векторов  . (Рис. 2)
. (Рис. 2)
 вычисляется по формуле
вычисляется по формуле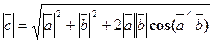
 , сумма которого с вычитаемым вектором
, сумма которого с вычитаемым вектором  . (Рис. 3)
. (Рис. 3)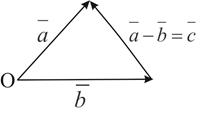
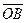 , совпадающий с одной диагональю параллелограмма, исходящей из точки О, равен сумме
, совпадающий с одной диагональю параллелограмма, исходящей из точки О, равен сумме 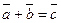 , а вектор
, а вектор  , совпадающий с другой диагональю равен разности
, совпадающий с другой диагональю равен разности  . (Рис. 4).
. (Рис. 4).
 вычисляется по формуле
вычисляется по формуле 

 , если l > 0
, если l > 0 , если l < 0
, если l < 0


