
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Колебательный контур с затуханием
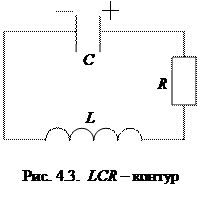
Колебательный контур без сопротивления - это идеальная модель. Реально LC -контур всегда обладает некоторым сопротивлением R хотя бы за счет подводящих проводов. Рассмотрим LC -контур с сопротивлением R (рис. 4.3). Такой контур называется контуром с затуханием или LCR -контуром. При замыкании обкладок заряженного конденсатора в контуре начинаются колебания. Однако теперь при протекании электрического тока за счет сопротивления R контур нагревается. Энергия электрического поля, первоначально запасенная в конденсаторе, постепенно переходит во внутреннюю энергию провода, амплитуды колебаний всех электрических величин уменьшаются вплоть до полного прекращения колебаний. Дифференциальное уравнение затухающих колебаний некоторой физической величины
Оно отличается от дифференциального уравнения гармонических колебаний (4.2) слагаемым ( В случае, когда затухание не слишком велико (выполняется условие
где
Вернемся к электромагнитным колебаниям в LCR -контуре. Поскольку внешние ЭДС в цепи не действуют, сумма падений напряжений на отдельных элементах контура равна нулю
Учитывая, что
Уравнение (4.12) по форме совпадает с дифференциальным уравнением (4.10). Отсюда можно сделать два основных вывода. 1). Процесс в LCR -контуре представляет собой затухающие колебания, зависимость заряда конденсатора от времени подобна (4.11):
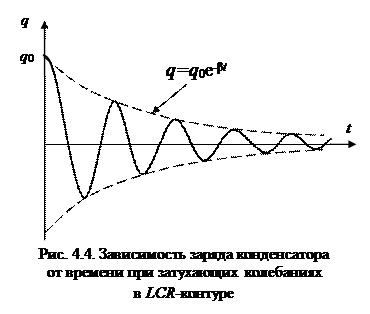
График функции (4.13) изображен на рис. 4.4. сплошной линией. Отдельно пунктирной линией показана зависимость амплитуды колебаний заряда от времени
2) Сравнение коэффициентов уравнений (4.10) и (4.12) показывает, что собственная циклическая частота колебаний Сформулируем несколько определений параметров затухающих колебаний. Время t, в течение которого амплитуда колебаний уменьшается в e»2,72 раз, называется временем затухания или временем релаксации. Отметим, что уменьшение амплитуды почти в 3 раза существенно, однако не означает полного прекращения колебаний. Время затухания t есть величина, обратная коэффициенту затухания b:
Докажем утверждение (4.14). Амплитуда колебаний в некоторый момент времени
Из формулы (4.14) следует, что Декрементом затухания
где Декремент затухания
Докажем формулу (4.16). Пусть Логарифмическим декрементом затухания называется величина
Пример 4.2. Определить число колебаний маятника за время затухания, если известен логарифмический декремент затухания Решение. Число колебаний можно найти, разделив полное время колебаний (в данном случае время затухания
4.3. Вынужденные колебания в LCR -контуре
Для того, чтобы поддерживать колебания в LCR -контуре, необходимо пополнять запасы энергии, непрерывно рассеиваемой в виде тепла на сопротивлении
где Согласно второму правилу Кирхгофа сумма падений напряжений на отдельных элементах контура равна внешней ЭДС:
Обозначая
Уравнение (4.18) называется дифференциальным уравнением вынужденных колебаний под действием синусоидальной ЭДС. С точки зрения математики уравнение (4.18) представляет собой линейное неоднородное (правая часть отлична от нуля) дифференциальное уравнение с постоянными коэффициентами. Решение данного уравнения представляет собой сумму двух слагаемых
Первое слагаемое – общее решение однородного уравнения (с правой частью, равной нулю), второе слагаемое – частное решение неоднородного уравнения. Первое слагаемое в точности совпадает с уравнением (4.13) и представляет собой затухающие колебания заряда конденсатора с циклической частотой
Характеристики вынужденных колебаний
График зависимости
Пример 4.3. Вывести формулу для величин резонансной частоты Решение. Для того чтобы найти точку максимума Далее, подставляя значение Если частота внешней силы Отношение резонансной амплитуды Используя формулы для
Поскольку
Чем меньше декремент затухания, тем выше добротность контура, и тем более он пригоден для радиотехники. Далее мы покажем, что добротность контура пропорциональна отношению энергии, запасённой в контуре, к её потерям за период колебаний (т.е. энергии, выделяющейся в контуре за период в виде тепла).
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 1032; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.137.164 (0.041 с.) |
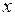 имеет вид
имеет вид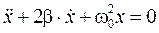 (4.10)
(4.10)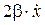 ), учитывающим силы сопротивления, действующие на маятник. Коэффициент b называется коэффициентом затухания. Если величина
), учитывающим силы сопротивления, действующие на маятник. Коэффициент b называется коэффициентом затухания. Если величина 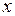 - смещение, её производная
- смещение, её производная 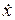 - скорость, тогда слагаемое
- скорость, тогда слагаемое 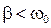 ), решение дифференциального уравнения (4.10) имеет вид:
), решение дифференциального уравнения (4.10) имеет вид: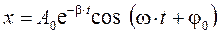 , (4.11)
, (4.11)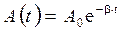 - амплитуда колебаний, уменьшающаяся со временем по экспоненциальному закону;
- амплитуда колебаний, уменьшающаяся со временем по экспоненциальному закону; 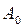 - начальная амплитуда колебаний;
- начальная амплитуда колебаний; 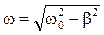 - циклическая частота колебаний;
- циклическая частота колебаний; 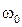 - собственная циклическая частота колебаний (частота, с которой колебался бы маятник, если бы сил сопротивления не было). Присутствие сил сопротивления уменьшает циклическую частоту колебаний и, соответственно, увеличивает период колебаний:
- собственная циклическая частота колебаний (частота, с которой колебался бы маятник, если бы сил сопротивления не было). Присутствие сил сопротивления уменьшает циклическую частоту колебаний и, соответственно, увеличивает период колебаний: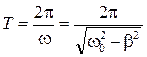 .
.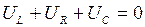
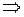
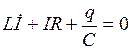 .
.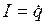 , получим:
, получим: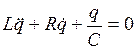
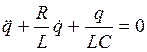 . (4.12)
. (4.12)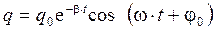 . (4.13)
. (4.13)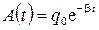 .
.
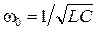 , а коэффициент затухания
, а коэффициент затухания 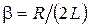 .
.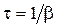 . (4.14)
. (4.14)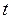 :
: 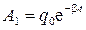 . Через время t, т.е. в момент времени
. Через время t, т.е. в момент времени 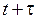 амплитуда колебаний
амплитуда колебаний 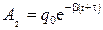 . По определению величины t
. По определению величины t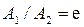
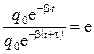
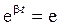
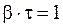
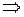
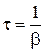 .
.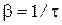 . Таким образом, коэффициент затухания – это величина, обратная времени затухания, т.е. времени, за которое амплитуда уменьшается в е раз.
. Таким образом, коэффициент затухания – это величина, обратная времени затухания, т.е. времени, за которое амплитуда уменьшается в е раз.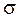 называется величина, равная отношению амплитуд следующих друг за другом колебаний:
называется величина, равная отношению амплитуд следующих друг за другом колебаний: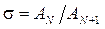 (4.15)
(4.15)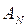 - амплитуда
- амплитуда 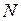 -го колебания,
-го колебания, 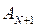 - амплитуда
- амплитуда 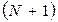 -го колебания.
-го колебания.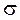 связан с коэффициентом затухания
связан с коэффициентом затухания 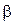 и периодом колебаний
и периодом колебаний 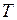 :
: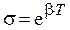 (4.16)
(4.16)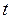 , тогда
, тогда 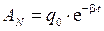 . Поскольку (
. Поскольку (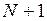 )-е и
)-е и 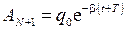 . Тогда
. Тогда 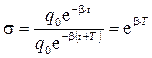 .
.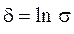 . Из формулы (4.16) следует:
. Из формулы (4.16) следует: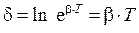 . (4.17)
. (4.17)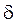 .
.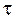 ) на время одного колебания, т.е. на период
) на время одного колебания, т.е. на период 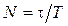 . Далее, используя формулу (4.14), получаем ответ:
. Далее, используя формулу (4.14), получаем ответ: 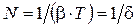 . Следствие:
. Следствие: 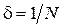 , т.е. логарифмический декремент затухания – есть величина, обратная числу колебаний за время затухания.
, т.е. логарифмический декремент затухания – есть величина, обратная числу колебаний за время затухания.
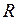 . Это можно с помощью воздействия на контур внешней периодической электродвижущей силы (рис. 4.5). При этом в контуре возникнут вынужденные колебания. Будем рассматривать синусоидальную ЭДС, т.е. ЭДС, зависящую от времени по закону синуса (или косинуса):
. Это можно с помощью воздействия на контур внешней периодической электродвижущей силы (рис. 4.5). При этом в контуре возникнут вынужденные колебания. Будем рассматривать синусоидальную ЭДС, т.е. ЭДС, зависящую от времени по закону синуса (или косинуса):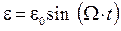 ,
,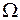 - циклическая частота колебаний ЭДС.
- циклическая частота колебаний ЭДС.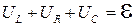
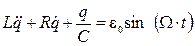
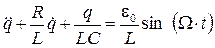 .
.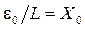 и учитывая, что
и учитывая, что 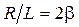 ,
, 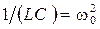 , получим
, получим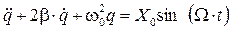 . (4.18)
. (4.18)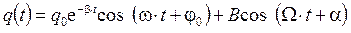 .
.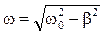 . Второе слагаемое соответствует собственным вынужденным колебаниям заряда с циклической частотой вынуждающей силы
. Второе слагаемое соответствует собственным вынужденным колебаниям заряда с циклической частотой вынуждающей силы 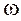 и
и 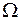 . Такой режим колебаний называется переходным. Первое слагаемое экспоненциально затухает за время по порядку величины, равное времени затухания
. Такой режим колебаний называется переходным. Первое слагаемое экспоненциально затухает за время по порядку величины, равное времени затухания 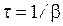 . Переходный режим заканчивается и наступает режим установившихся вынужденных колебаний с частотой вынуждающей силы
. Переходный режим заканчивается и наступает режим установившихся вынужденных колебаний с частотой вынуждающей силы 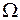
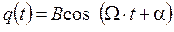 . (4.19)
. (4.19)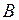 и a зависят, во-первых, от параметров вынуждающей силы
и a зависят, во-первых, от параметров вынуждающей силы 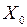 и
и 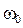 и
и 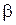 , но не зависят от начальных условий. Подставляя функцию
, но не зависят от начальных условий. Подставляя функцию 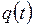 (4.19) в уравнение (4.18), можно найти выражение для амплитуды вынужденных колебаний
(4.19) в уравнение (4.18), можно найти выражение для амплитуды вынужденных колебаний 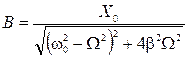 , (4.20)
, (4.20)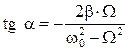 . (4.21)
. (4.21)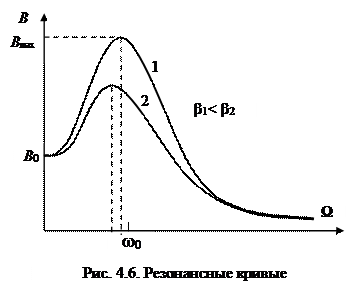
 (4.20), показанный на рис. 4.6, называется резонансной кривой. Резонансная кривая имеет максимум. Максимальное значение амплитуды установившихся колебаний достигается при резонансной частоте
(4.20), показанный на рис. 4.6, называется резонансной кривой. Резонансная кривая имеет максимум. Максимальное значение амплитуды установившихся колебаний достигается при резонансной частоте 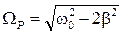 , которая при небольшом затухании мало отличается от собственной циклической частоты колебаний системы
, которая при небольшом затухании мало отличается от собственной циклической частоты колебаний системы 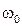 . Таким образом, резонанс наступает при условии совпадения частоты внешней синусоидальной силы и собственной частоты колебательной системы
. Таким образом, резонанс наступает при условии совпадения частоты внешней синусоидальной силы и собственной частоты колебательной системы 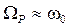 . Кривая 1 на рис. 4.6 относится к колебательной системе с меньшим затуханием. Чем меньше коэффициент затухания, тем ближе резонансная частота к собственной частоте системы и больше значение максимальной амплитуды, т.е. острее и уже пик резонансной кривой. Отметим, что ширина максимума на уровне
. Кривая 1 на рис. 4.6 относится к колебательной системе с меньшим затуханием. Чем меньше коэффициент затухания, тем ближе резонансная частота к собственной частоте системы и больше значение максимальной амплитуды, т.е. острее и уже пик резонансной кривой. Отметим, что ширина максимума на уровне 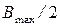 равна коэффициенту затухания:
равна коэффициенту затухания: 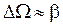 .
.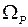 и максимальной амплитуды B max (рис. 4.6).
и максимальной амплитуды B max (рис. 4.6).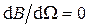 . В результате получится
. В результате получится 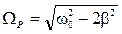 .
.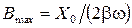 , где
, где 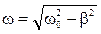 - циклическая частота затухающих колебаний.
- циклическая частота затухающих колебаний.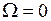 , то значение амплитуды по формуле (4.20)
, то значение амплитуды по формуле (4.20) 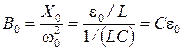 , что соответствует статическому заряду конденсатора, приобретаемому при подключении его к постоянной ЭДС
, что соответствует статическому заряду конденсатора, приобретаемому при подключении его к постоянной ЭДС 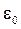 .
.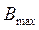 к величине статического отклонения колебательной системы
к величине статического отклонения колебательной системы 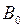 называется добротностью колебательной системы
называется добротностью колебательной системы 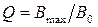 .
.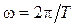 , получим:
, получим: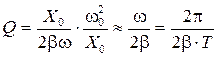 .
.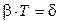 - логарифмический декремент затухания, то:
- логарифмический декремент затухания, то: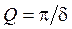 . (4.22)
. (4.22)


