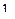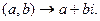Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторы и векторные пространства
Первоначально вектором называли направленный отрезок, прикрепленный к одной точке. Для иллюстрации физических величин, имеющих не только величину, но и направление. Эти величины можно складывать по правилу параллелограмма, вычитать, умножать на числа. При этом, каковы бы ни были векторы
Позже вектор сделали свободным от точки прикрепления. Свободный вектор- совокупность всевозможных направленных отрезков, параллельных между собой, имеющих одну и ту же длину и одно и тоже направление. Такие отрезки называются эквивалентными. Свободные векторы задаются с помощью координат, т.е. проекций на координатные оси X и Y. В пространстве направленный отрезок имеет три координаты – проекции на координатные оси X,Y,Z. Вектор можно заменить совокупностью координат. На плоскости это пары чисел
Такая точка зрения на векторы оказалась очень плодотворной. Под определение вектора попало много физических и математических объектов. Например, всякое элементарное событие, происходящее в пространстве в точке с координатами (x, y, z) в момент времени t, можно рассматривать как четырехмерный вектор (x, y, z, t). Получается пространство событий. Количество координат вектора называется размерностью. Векторы одной размерности можно складывать и умножать на числа по тем же правилам, что двумерные и трехмерные. И при любой размерности будут выполняться свойства (2). Векторным пространством называется всякое множество, для элементов которого определены операции сложения и умножения на числа таким образом, что выполняются свойства (2). Группы Три свойства операции сложения: - ассоциативность: (а + в) + с = а + (в + с), - наличие нейтрального элемента: а + 0 = а, (3) (3) - существование противоположных элементов: а + (- а) = 0. справедливы для любого кольца и любого векторного пространства. Пример: Запишем по порядку числа 1, 2, 3, 4, 5, 6. Перепутаем их каким- либо образом: 2, 3, 5, 1, 6, 4.
Запишем в виде таблицы:
Эта таблица задает некоторую функцию, если считать, что верхний ряд- значения х, а нижний – значения у. Такая функция называется подстановкой или перестановкой из шести элементов и действует так: Результат последовательного действия двух перестановок тоже будет перестановкой:
т.е. Любые три перестановки
Умножение тождественной перестановки
на любую другую перестановку дает следующее:
Для каждой перестановки S можно найти обратную ей
отсюда
Если в равенствах (4) - (6) заменить символ Все сказанное относится и к подстановкам из любого числа элементов. Группой называется множество, на котором задана операция, свойства которой описываются аксиомами (3). Множество всех подстановок из n элементов образует группу относительно операции композиции (умножения). В этой группе n! элементов, она называется симметричной группой и обозначается Множество Z (Q, R) является группой относительно сложения. Комплексные числа Множество R действительных чисел ограничено тем, что квадратные корни можно извлекать только из положительных чисел. Это создает большие неудобства при решении, например, алгебраических уравнений. Поэтому поле действительных чисел было расширено добавлением нового элемента
Для каждого комплексного числа можно найти обратное:
Операции сложения и умножения комплексных чисел подчиняются аксиомам (1), поэтому комплексное число образует поле. Открытие комплексных чисел позволило решить проблему алгебраических уравнений. Главный результат сформулирован в основной теореме алгебры: Всякое алгебраическое уравнение степени n с комплексными коэффициентами имеет ровно n комплексных корней. (Гаусс). Иоганн Бернулли и Леонард Эйлер открыли формулу
из которой при Каждое комплексное число геометрически представлено на плоскости точкой с координатами Информатизация общества
|
||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 83; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.137.218 (0.007 с.) |
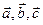 и числа
и числа 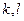 всегда выполняются равенства:
всегда выполняются равенства: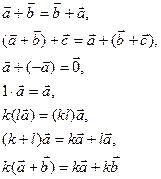 (2)
(2) в пространстве тройки чисел
в пространстве тройки чисел  . Сложение векторов и умножение на число заменяется соответствующими действиями над координатами:
. Сложение векторов и умножение на число заменяется соответствующими действиями над координатами: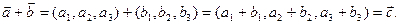
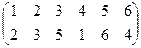
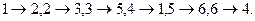 Всего подстановок 6! = 720.
Всего подстановок 6! = 720.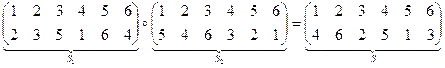
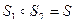 Это композиция, или сложная функция S, называется произведением
Это композиция, или сложная функция S, называется произведением 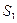 и
и 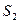 .
.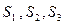 можно перемножить так: либо
можно перемножить так: либо 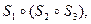 либо
либо 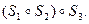 Результат один и тот же, поэтому можно записать:
Результат один и тот же, поэтому можно записать: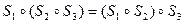 (4)
(4)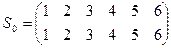
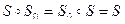 (5)
(5)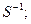 которая действует так: если S переводит
которая действует так: если S переводит 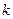 в
в 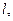 то
то 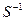 переводит
переводит 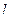 в
в 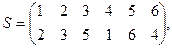
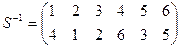
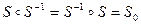 (6)
(6) на + и вместо
на + и вместо 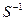 написать
написать 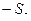 то эти равенства совпадут с равенствами (3).
то эти равенства совпадут с равенствами (3).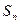 .
.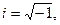 который называется мнимой единицей. Мнимая единица не является действительным числом, но на нее распространили все алгебраические свойства действительных чисел. В результате появились новые элементы, которые записывают в виде
который называется мнимой единицей. Мнимая единица не является действительным числом, но на нее распространили все алгебраические свойства действительных чисел. В результате появились новые элементы, которые записывают в виде 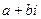 и называют комплексными числами. Если
и называют комплексными числами. Если 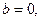 то комплексное число является действительным. Поэтому действительные числа составляют часть комплексных чисел. По определению
то комплексное число является действительным. Поэтому действительные числа составляют часть комплексных чисел. По определению 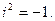 Комплексные числа можно складывать и умножать:
Комплексные числа можно складывать и умножать: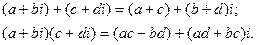

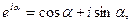
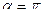 следует
следует 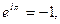 что связывает мнимую единицу
что связывает мнимую единицу 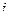 с числами
с числами 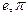 и
и