
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деление комплексных чисел в алгебраической форме
Деление комплексных чисел Деление комплексных чисел в алгебраической форме Определение Частным двух комплексных чисел
На практике деление комплексных чисел проводят по следующей схеме: 1. сначала делимое и делитель умножают на число, комплексно сопряженное делителю, после чего делитель становится действительным числом; 2. в числителе умножают два комплексных числа; 3. полученную дробь почленно делят. Пример Задание. Найти частное Решение. Домножим и числитель, и знаменатель заданной дроби на число, комплексно сопряженное к знаменателю
Далее перемножаем комплексные числа как алгебраические двучлены, учитывая, что
Ответ. Деление комплексных чисел в геометрической форме Если надо поделить комплексные числа
То есть модуль частного двух комплексных чисел равен частному модулей, а аргумент - разности аргументов делимого и делителя. Пример Задание. Найти частное Решение. Искомое частное
Ответ.
Выводы В данной статье введено понятие комплексного числа и рассмотрены основные его свойства. Подробно рассмотрено представление комплексного числа на плоскости, приведена формула Эйлера показательной формы комплексного числа. Рассмотрены основные арифметические операции над комплексными числами.
Любые вопросы и пожелания вы можете оставить в гостевой книге, на форуме, или прислать по электронной почте admin@dsplib.ru
Наверх Вернуться к списку статей |

|
Деление комплексных чисел
Деление комплексных чисел в алгебраической форме
Определение
Частным двух комплексных чисел 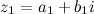 и
и  называется число
называется число  , которое задается соотношением:
, которое задается соотношением:
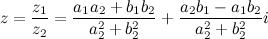
На практике деление комплексных чисел проводят по следующей схеме:
1. сначала делимое и делитель умножают на число, комплексно сопряженное делителю, после чего делитель становится действительным числом;
2. в числителе умножают два комплексных числа;
3. полученную дробь почленно делят.
Пример
Задание. Найти частное 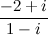
Решение. Домножим и числитель, и знаменатель заданной дроби на число, комплексно сопряженное к знаменателю 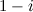 , это будет
, это будет  , тогда имеем:
, тогда имеем:

Далее перемножаем комплексные числа как алгебраические двучлены, учитывая, что  :
:
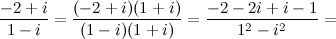

Ответ. 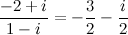
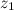 и
и  в геометрической форме:
в геометрической форме: 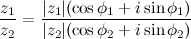 , то искомое число
, то искомое число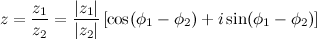
 , если
, если  , а
, а 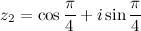
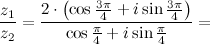
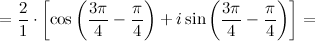
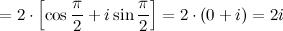
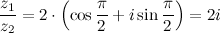
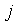 , которая существует на множестве комплексных чисел, но не существует на множестве действительных. Мнимая единица удовлетворяет равенству:
, которая существует на множестве комплексных чисел, но не существует на множестве действительных. Мнимая единица удовлетворяет равенству:
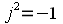 .
.
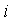 . Тогда комплексное число
. Тогда комплексное число 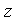 можно представить в виде:
можно представить в виде: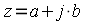 ,
,
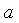 носит название действительной части или реальной части и обозначается
носит название действительной части или реальной части и обозначается 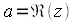 , а
, а 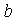 носит название мнимой части и обозначается как
носит название мнимой части и обозначается как  . Графически все множество действительных чисел можно представить на бесконечной числовой прямой, при этом комплексные числа можно трактовать как расширение числовой прямой до комплексной плоскости, а каждое комплексное число можно представить как точку на комплексной плоскости (смотри рисунок 1). При этом все множество действительных чисел будет представляться прямой на комплексной плоскости.
. Графически все множество действительных чисел можно представить на бесконечной числовой прямой, при этом комплексные числа можно трактовать как расширение числовой прямой до комплексной плоскости, а каждое комплексное число можно представить как точку на комплексной плоскости (смотри рисунок 1). При этом все множество действительных чисел будет представляться прямой на комплексной плоскости.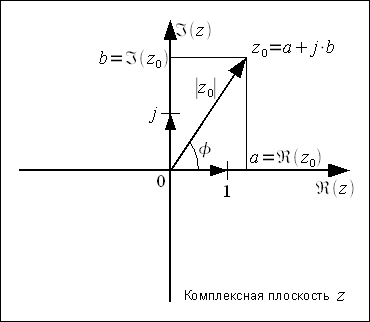
 делится прямыми реальной части
делится прямыми реальной части  (прямой действительных чисел) и прямой мнимых чисел
(прямой действительных чисел) и прямой мнимых чисел 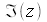 на четыре четверти. Любое комплексное число
на четыре четверти. Любое комплексное число 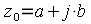 ,будет представляться точкой на комплексной плоскости с координатами
,будет представляться точкой на комплексной плоскости с координатами  и
и 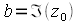 . Если число не содержит мнимой части, то оно действительное и находится на прямой
. Если число не содержит мнимой части, то оно действительное и находится на прямой 


