
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа. Определение длины световой волны при помощи дифракционной решетки
Цель работы: изучение явления дифракции и определение длины волны с помощью дифракционной решетки.
Теоретические сведения
Явление дифракции света заключается в отклонении от прямолинейного распространения света вблизи непрозрачных препятствий. Дифракция обусловлена взаимодействием световых волн с краями препятствий. Строгий расчет картины дифракции на основе электромагнитной теории света сложен, но можно оценить результат дифракции, пользуясь принципом Гюйгенса-Френеля. Согласно принципу Гюйгенса-Френеля каждая точка волновой поверхности (т.е. поверхности с одинаковой фазой колебаний) является самостоятельным источником вторичных волн, распространяющихся со скоростью света. Вторичные волны являются когерентными. Результат действия волновой поверхности в конкретной точке определяется интерференцией вторичных волн.
Дифракция от одной щели
Рассмотрим узкую щель шириной АВ=а, освещенную пучком параллельных монохроматических лучей с длиной волны λ (рисунок 10.1). Согласно принципу Гюйгенса-Френеля каждая точка щели, до которой дошел свет, становится источником вторичных волн, распространяющихся за щелью во всех направлениях. Дифрагирующие волны когерентны и при наложении интерферируют. Результат интерференции в виде периодического распределения интенсивности наблюдается на экране Э, расположенном в фокальной плоскости линзы Л, поставленной за щелью.
Все дифрагирующие волны, идущие от щели, можно мысленно разделить на системы параллельных лучей. Лучи каждой системы образуют с нормалью угол α и собираются на экране в побочном фокусе линзы Л. Результат наложения волн можно оценить по оптической разности хода лучей, исходящих из крайних точек щели А и В. Для нахождения оптической разности хода построим фронт волны, дифрагирующей под углом α, для чего опустим перпендикуляр ВС из точки В на луч АС. Тогда оптическая разность хода крайних лучей будет равна:
так как Пусть разность хода между крайними лучами равна длине волны λ, т.е.
В этом случае разность хода между лучами, идущими от точек А и О щели, равна λ/2. Аналогично, разность хода между лучами, идущими от точек О и В, равна λ/2. Для любого луча, выходящего из левой половинки щели (АО), можно найти луч из правой половины (ОВ) такой, что разность хода между ними будет равна λ/2, и при наложении они погасят друг друга. Таким образом, все лучи левой половины пучка погасят все лучи правой половины, и соответствующее место экрана будет темным, т.е. условие (9.1.) является условием первого минимума. Можно показать, что если
где к=1,2,…кmax, то в соответствующих точках экрана будет также наблюдаться минимум. Число к называют порядком минимума. кmax – наибольший порядок минимума, он определяется из условия: Условие дифракционных максимумов записывают в виде
Дифракционная решетка
Плоская прозрачная дифракционная решетка представляет собой систему параллельных щелей одинаковой ширины а, находящихся на равных расстояниях друг от друга в и лежащих в одной плоскости. Она изготавливается путем нанесения непрозрачных штрихов на прозрачной пластине, либо шероховатых, рассеивающих штрихов на тщательно отполированной металлической пластине и применяется в проходящем или отраженном свете. Дифракционная картина при прохождении света через дифракционную решетку (систему из N щелей) значительно усложняется. Колебания, приходящие от разных щелей, являются когерентными. Условие ослабления колебаний от одной щели (10.2) является условием ослабления колебаний для каждой щели дифракционной решетки. Его поэтому называют условием главных минимумов:
которое называют условием главных максимумов, а m – порядок главного максимума. Наибольший порядок главного максимума определяется из условия
Величину
Условие наибольшего ослабления колебаний от всех щелей, называемое условием дополнительных минимумов, наблюдается в том случае, когда оптическая разность хода волн от крайних точек соседних щелей равна
где Из условия (10.7) следует, что между соседними главными максимумами наблюдается N-1 дополнительных минимумов и N-2 дополнительных максимумов. При большом числе щелей в решетке интенсивность дополнительных максимумов настолько мала, что они практически не обнаруживаются, и на экране наблюдаются только главные максимумы, расположение которых зависит от постоянной решетки и длины волны падающего на решетку монохроматического света. При освещении решетки белым светом вместо одиночных главных максимумов первого и более высокого порядков появляются спектры. Максимум нулевого порядка в спектр не разлагается, т.к. под углом α=0 наблюдается максимум для любых длин волн. В спектре каждого порядка, как следует из (10.6), максимум для более коротких волн наблюдается ближе к нулевому максимуму, для более длинных – дальше от него. Способность дифракционной решетки разлагать падающий на нее немонохроматический свет в спектр характеризуется угловой или линейной дисперсией. Угловая дисперсия решетки характеризуется углом, на который смещается максимум спектральной линии при изменении длины волны на единицу
где Δα – угол, на который смещается максимум при изменении длины волны спектральной линии на Δλ. Угловая дисперсия зависит от порядка спектра m и постоянной решетки d
Линейная дисперсия дифракционной решетки определяется соотношением
где Δl – расстояние между двумя спектральными линиями, длины волн которых отличаются на Δλ. Другой характеристикой решетки является ее разрешающая способность. Она определяется отношением длины волны в данной области спектра к минимальному интервалу длин волн, разрешаемому с помощью данной решетки
Разрешающая способность зависит от порядка спектра m и общего числа щелей N в решетке. Способность дифракционной решетки разлагать белый свет в спектр дает возможность использовать ее в качестве диспегирующего устройства в спектральных приборах. Зная постоянную решетки и измерив угол дифракции, можно определить спектральный состав излучения неизвестного источника. В данной лабораторной работе дифракционная решетка используется для определения длины световой волны.
Описание установки
Для точного измерения углов дифракции в данной лабораторной работе используется прибор, называемый гониометром. Схематическое устройство гониометра приведено на рисунке 10.2.
Рисунок 10.2
Основные части гониометра: закрепленные на общей оси круг с делениями (лимб), коллиматор, зрительная труба и столик с дифракционной решеткой. Коллиматор предназначен для создания параллельного пучка лучей. Он состоит из наружного тубуса, в котором закреплена линза Л, и внутреннего с входной щелью S. Ширина щели может регулироваться микрометрическим винтом. Щель располагается в фокальной плоскости линзы Л, поэтому из коллиматора выходит параллельный пучок лучей. Зрительная труба также состоит из двух тубусов: наружного, в котором закреплен объектив M, и внутреннего с закрепленным в нем окуляром N. В фокальной плоскости объектива располагается визирная нить. Если прибор отъюстирован, то визирная нить и изображение освещенной щели коллиматора в поле зрения окуляра видны отчетливо. Лимб разделен на 360 градусов, расстояние между градусными делениями разделено на две части по 30 минут каждая, т.е. цена деления лимба 30 минут. Для более точного отсчета углов имеется нониус Н, имеющий 30 делений, общая длина которых составляет 29 делений лимба. Поэтому точность деления нониуса Dl равна:
так как Если цена деления лимба 30 минут и нониус содержит 30 делений, то точность деления нониуса равна одной минуте. Отсчет угла гониометра производят следующим образом. Отмечают число целых делений по шкале лимба напротив нуля нониуса (отсчет берется от нуля нониуса), затем делают отсчет по шкале нониуса: выбирают такое деление нониуса, которое совпадает с каким-либо делением шкалы лимба. Измеренный угол будет равен:
где k – число делений по шкале лимба; m – число делений нониуса до деления, точно совпадающего с делением шкалы лимба; l – цена деления лимба; Δl – точность нониуса. Для случая, приведенного на рисунке 10.3, число делений лимба до 0 нониуса 19,5, что соответствует 19 градусам и 30 минутам.
Рисунок 10.3 Нуль нониуса не совпадает с делениями лимба, совпадает пятое деление нониуса. Следовательно, угол отсчета равен 19 градусам и 35 минутам.
На столике гониометра закреплена дифракционная решетка так, что ее плоскость, обращенная к зрительной трубе, совпадает с диаметром столика. Столик гониометра устанавливается таким образом, чтобы дифракционная решетка была перпендикулярна оси коллиматора. Щель коллиматора освещается ртутной лампой. Если зрительная труба установлена по оси коллиматора, то в поле зрения видно изображение щели – главный максимум нулевого порядка. При смещении зрительной трубы вправо или влево можно увидеть сначала синюю, затем зеленую и желтую линии спектра первого порядка. При дальнейшем повороте зрительной трубы в ее поле зрения окажутся в той же последовательности спектральные линии второго порядка, затем третьего и т.д. Для определения угла дифракции какой-либо волны необходимо навести визирную нить зрительной трубы на середину линии соответствующего цвета слева от нулевого максимума, закрепить винт, фиксирующий положение трубы, и произвести отсчет угла, например b1, затем, освободив винт, навести визирную нить зрительной трубы на середину линии такого же цвета в том же порядке спектра справа от нулевого максимума и, закрепив винт, сделать отсчет угла b2. Разность отсчетов даст удвоенный угол дифракции (рисунок 10.4), а угол дифракции будет равен:
Рисунок 10.4
10.5 Приборы и материалы: дифракционная решетка, осветитель, гониометр. Порядок выполнения работы
Включить вентилятор и ртутную лампу. Направить коллиматор гониометра на “окно” ртутной лампы. Проверить, стоит ли дифракционная решетка перпендикулярно оси коллиматора. Навести зрительную трубу на центральный дифракционный максимум (максимум нулевого порядка) – изображение щели коллиматора. Если изображение щели неотчетливо, слегка перемещая внутренний тубус с помощью винта, добиться отчетливого изображения щели. Отчетливое изображение визирной нити достигается перемещением окуляра зрительной трубы. Навести визирную нить на желтую линию в спектре второго порядка слева от нулевого максимума и, закрепив зрительную трубу винтом, произвести отсчет угла по шкале лимба и нониуса b1. Произвести те же измерения для зеленой и синей линии второго порядка и для всех трех линий первого порядка. Перевести зрительную трубу на спектры справа от нулевого максимума и произвести измерения углов дифракции b2 для этих же линий в спектре первого и второго порядков. Повторить измерения 2 раза в том те порядке. Результаты измерений по мере их выполнения заносить в заранее заготовленную таблицу 10.1. Таблица 10.1
Определить углы дифракции по формуле (10.14), и занести в таблицу. Вычислить длины волн всех линий по формуле:
Значение постоянной решетки спросить у лаборанта или преподавателя. Оценить погрешность измерений.
Вопросы для самоподготовки
В чем суть явления дифракции света? Сформулировать принцип Гюйгенса-Френеля. Рассмотрите дифракцию от одной щели и дифракционной решетки. Чем отличается дифракционный спектр от спектра призмы? Что такое угловая и линейная дисперсия дифракционной решетки? Что такое разрешающая способность дифракционной решетки? Что такое гониометр? Рассмотрите его принципиальное устройство.
Техника безопасности
Перед включением вентилятора установить его так, чтобы лопасти не касались установки. При выполнении работы не касаться лопастей вентилятора. Ртутная лампа – источник ультрафиолетового излучения, поэтому необходимо избегать прямого попадания излучения в глаза. При выполнении работы строго выполнять порядок включения источника питания ртутной лампы: сначала включить вентилятор, а потом источник питания. Отключение производить в обратном порядке: сначала источник питания, а затем вентилятор.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 394; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.249.105 (0.039 с.) |

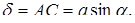
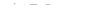 по построению.
по построению. (10.1)
(10.1)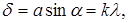 (10.2)
(10.2)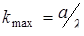 .
. (10.3)
(10.3) Кроме того, происходит взаимодействие колебаний одной щели с колебаниями других щелей. Взаимное усиление колебаний, исходящих из всех щелей происходит при условии
Кроме того, происходит взаимодействие колебаний одной щели с колебаниями других щелей. Взаимное усиление колебаний, исходящих из всех щелей происходит при условии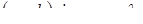 (10.4)
(10.4)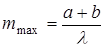 (10.5)
(10.5)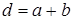 называют периодом решетки, поэтому формулу (10.4) можно записать в виде
называют периодом решетки, поэтому формулу (10.4) можно записать в виде (10.6)
(10.6)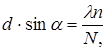 (10.7)
(10.7)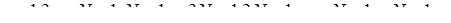 – порядок дополнительных минимумов, N – число щелей решетки.
– порядок дополнительных минимумов, N – число щелей решетки. (10.8)
(10.8)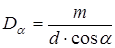 . (10.9)
. (10.9)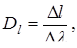 (10.10)
(10.10)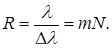 (10.11)
(10.11)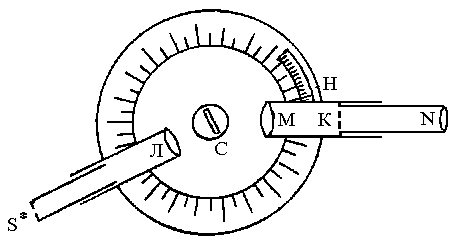
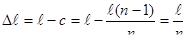 , (10.12)
, (10.12)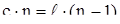 ,где l – цена деления лимба, с – цена деления нониуса.
,где l – цена деления лимба, с – цена деления нониуса.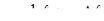 , (10.13)
, (10.13)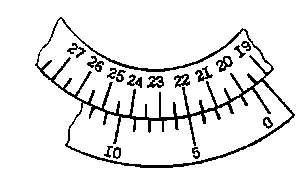
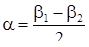 (10.14)
(10.14)
 . (10.15)
. (10.15)


