Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная параметрически заданной функции
Функция
Пример 3.4. Найти производную функции Решение. Функция задана параметрически, тогда по формулам параметрического дифференцирования (8) имеем:
Логарифмическое дифференцирование
Логарифмической производной положительной функции есть производная от логарифма данной функции. Пример 3.5. Найти производную функции Решение. Используем к данной функции логарифмическое дифференцирование. Логарифмируем обе части уравнения:
Дифференцируем обе части уравнения:
Пример 3.6. Найти производную функции Решение. Логарифмируем обе части уравнения, получим:
Производная функции старших порядков
Пример 3.7. Найти производные
Решение. Имеем:
Пример 3.8. Найти дифференциал dy функции: Решение.
Пример 9. Найти предел:
Решение. Используем правило Лопиталя:
(использование предельного перехода приводит к неопределенности вида
Основные понятия 1. Если производная дифференцируемой функции положительна внутри некоторого интервала 2. Если производная дифференцируемой функции отрицательна внутри интервала
Достаточные условия экстремума функции.
Аналогичное утверждение можно сформулировать о наименьшем значении функции: оно достигается на одно из концов данного промежутка или в такой внутренней точке, которая есть минимумом.
Исследование функции План исследования функций 1. Найти область определения функции. 2. Проверить четность (нечетность) и периодичность функции. 3. Найти точки разрыва функции и определить их вид. 4. Определить точки пересечения функции с осями координат. 5. Найти точки экстремума, интервалы возрастания и убывания функции. 6. Найти точки перегиба, интервалы выпуклости и вогнутости функции. 7. Найти асимптоты. 8. Построить график. Пример 3.10. Исследовать на экстремум функцию Решение. Область определения функции: Найдем производную функции
Используем необходимое условие экстремума функции:
Критическая точка Рассмотрим интервалы
Таблица 3.1. – Исследование функции с помощью первой производной
Из таблицы 3.1 видно, что в точке
Пример 3.11. Найти наибольшее и наименьшее значения функции Решение. Находим производную и критические точки функции:
Критическая точка Вычислим значение функции в критических точках – Следовательно, наибольшее значение функции на заданном отрезке Пример 3.12. Найти асимптоты графика функции Решение. Функция определена при всех значениях То есть, прямая Горизонтальных асимптот график не имеет, так как Найдем наклонную асимптоту:
Следовательно,
Пример 3.13. Исследовать функцию Решение. 1. Находим область определения функции. ОДЗ: Функция существует при всех значениях 2. Функция общего вида, не периодическая. Поскольку 3. Точка
То есть, точка 4. Находим точки перегиба графика функции с осями координат: с осью Ох: с осью Оу: 5. Находим точки экстремума, интервалы возрастания и убывания функции, результаты заносим в таблицу:
Исследуем критические точки на экстремум:
Таблица 3.2 – Исследование функции с помощью второй производной
Проходя через точку Функция убывает при Функция возрастает при 6. Точки перегиба и интервалы выпуклости и вогнутости находим из второй производной:
При
Таблица 3.3 – Исследование функцию с помощью второй производной
Вторая производная, проходя через Найдем ее ординату: Таким образом, График функции вогнутый при График функции выпуклый при 7. Прямая Так как 8. Строим график функции.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 82; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.240.21 (0.052 с.) |
 от
от 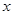 задана параметрическими уравнениями:
задана параметрическими уравнениями: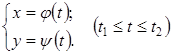 , тогда производная равна:
, тогда производная равна:
 , если она задана в параметрическом виде:
, если она задана в параметрическом виде: 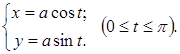
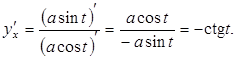
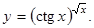


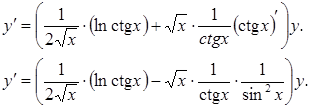

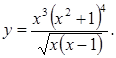
 Дифференцируем обе части уравнения:
Дифференцируем обе части уравнения:

 :
: 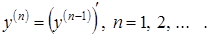
 функции
функции .
.
 ,
,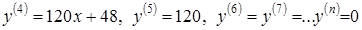 .
.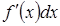 называется дифференциалом функции
называется дифференциалом функции 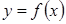 и его обозначают символом dy, то есть:
и его обозначают символом dy, то есть:

 -го порядка имеет вид:
-го порядка имеет вид:


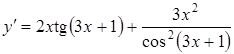 , тогда
, тогда  .
.


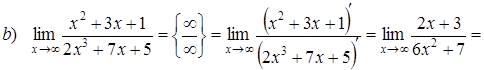
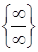 , а поэтому используем правило Лопиталя повторно):
, а поэтому используем правило Лопиталя повторно): .
. , то функция возрастает на этом интервале.
, то функция возрастает на этом интервале. , то функция убывает на этом интервале.
, то функция убывает на этом интервале. имеет максимум
имеет максимум 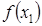 , если в некоторой окрестности точки
, если в некоторой окрестности точки  выполняется неравенство
выполняется неравенство 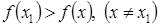 .
.
 имеетминимум
имеетминимум  если в некоторой окрестности точки
если в некоторой окрестности точки  выполняется неравенство
выполняется неравенство 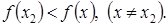
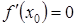 или не существует.
или не существует.
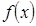 непрерывна на некотором интервале, в котором содержится критическая точка
непрерывна на некотором интервале, в котором содержится критическая точка 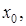 и дифференцируема во всех точках этого интервала (кроме, возможно, той точки
и дифференцируема во всех точках этого интервала (кроме, возможно, той точки  ). Если при переходе слева направо через эту точку производная:
1) изменяет знак с «+» на «–», то в точке
). Если при переходе слева направо через эту точку производная:
1) изменяет знак с «+» на «–», то в точке  функция имеет максимум;
2) изменяет знак «–» на «+», то в точке
функция имеет максимум;
2) изменяет знак «–» на «+», то в точке 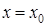 функция имеет минимум;
3) не изменяет своего знака, то в точке
функция имеет минимум;
3) не изменяет своего знака, то в точке  функция экстремума не имеет.
функция экстремума не имеет.
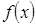 в некоторой точке
в некоторой точке  ее первая производная
ее первая производная 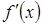 равна нулю, а вторая производная
равна нулю, а вторая производная  существует и отлична от нуля, то есть
существует и отлична от нуля, то есть 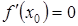 ,
, 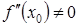 , тогда:
1) если
, тогда:
1) если 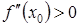 , то в точке
, то в точке 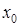 функция
функция  то в точке
то в точке  то в точке
то в точке 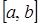 достигает своего наибольшего значения на одном из концов этого промежутка или в такой точке, которая является точкой максимума.
достигает своего наибольшего значения на одном из концов этого промежутка или в такой точке, которая является точкой максимума.
 для функции
для функции 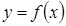 вторая производная положительна
вторая производная положительна  , то график функции вогнутый.
2) Если во всех точках промежутка
, то график функции вогнутый.
2) Если во всех точках промежутка 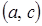 вторая производная отрицательна
вторая производная отрицательна 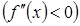 , то график функции выпуклый.
, то график функции выпуклый.
 , если хотя бы один из односторонних пределов в точке
, если хотя бы один из односторонних пределов в точке  равен бесконечности, то есть
равен бесконечности, то есть 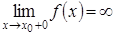 или
или  , или
, или  .
.
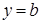 называется горизонтальной асимптотой графика функции
называется горизонтальной асимптотой графика функции  , если существует конечный предел функции при
, если существует конечный предел функции при 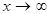 , то есть
, то есть 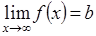 .
.
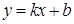 называется наклоннойасимптотой графика функции
называется наклоннойасимптотой графика функции
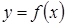 , если
, если 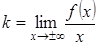 ,
,  .
.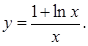
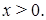
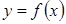 и ее стационарные точки:
и ее стационарные точки:



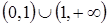 и исследуем знак слева и справа от каждой критической точки. Результаты занесем в таблицу 2.
и исследуем знак слева и справа от каждой критической точки. Результаты занесем в таблицу 2.


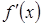


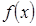
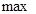
 функция имеет максимум.
функция имеет максимум.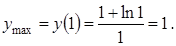
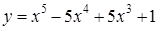 на отрезке
на отрезке 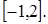


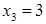 не принадлежит заданному отрезку, то есть
не принадлежит заданному отрезку, то есть 
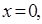
 и на концах отрезка –
и на концах отрезка – 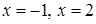 :
: 



 наименьшее
наименьшее 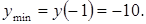

 за исключением значения
за исключением значения 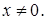 Поскольку при
Поскольку при 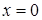 знаменатель дроби равен нулю, то в точке
знаменатель дроби равен нулю, то в точке 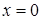 функция имеет разрыв второго рода.
функция имеет разрыв второго рода.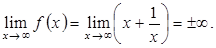


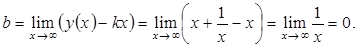

 и построить ее график.
и построить ее график.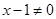
 .
. за исключением значения
за исключением значения 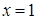 .
.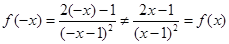 , значит, функция
, значит, функция 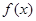 не является четной и
не является четной и 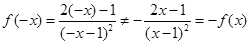 , значит
, значит  не является нечетной, таким образом, функция
не является нечетной, таким образом, функция  - функция общего вида.
- функция общего вида.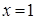 является точкой разрыва функции. Исследуем ее характер:
является точкой разрыва функции. Исследуем ее характер: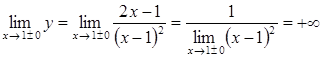 .
.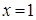 – точка разрыва второго рода.
– точка разрыва второго рода.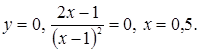


 – критическая точка. При
– критическая точка. При  первая производная функции не существует, но в этой точке сама функция тоже не существует.
первая производная функции не существует, но в этой точке сама функция тоже не существует.





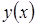
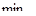
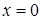 функция имеет минимум:
функция имеет минимум: 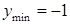 .
.


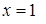 вторая производная функции не существует, но в этой точке не существует и сама функция. Исследуем точку
вторая производная функции не существует, но в этой точке не существует и сама функция. Исследуем точку  и найдем значение
и найдем значение  слева и справа от этой точки. Результаты исследования заносим в таблицу 3.3.
слева и справа от этой точки. Результаты исследования заносим в таблицу 3.3.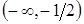
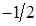

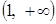

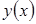
 , изменяет знак.
, изменяет знак. .
.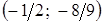 – точка перегиба.
– точка перегиба.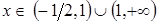 .
.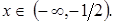
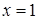 – вертикальная асимптота.
– вертикальная асимптота. то наклонных асимптот нет.
то наклонных асимптот нет.