Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розвязування раціональних нерівностей вищих степенів методом інтервалів
Будемо розглядати розв’язання раціональних нерівностей методом інтервалів. Існують різні схеми реалізації цього методу. Розглянемо одну з цих схем, допускаючи, що розв’язується нерівність 1.Перенести всі члени нерівності вліво:
2.Ліву частину отриманої нерівності привести до спільного знаменника:
3.Багаточлени
При скороченні треба мати на увазі, що:
4. Виключити з розкладення нелінійні множники. Це виключення виконується таким чином. Якщо в розкладенні є множник,
Якщо в розкладенні є множник
Нелінійний множник
5. На числовій осі відмітимо точки, в яких обертаються в нуль всі множники, що стоять в чисельнику і знаменнику лівої частини нерівності, отриманої в результаті виконання пунктів «1» - «4». При цьому, якщо нерівність нестрога, точки, які відповідають множникам чисельника будемо визначати зафарбованими кружками, а точки, що відповідають множникам знаменника світлими. Якщо нерівність строга, всі точки відмічаються світлими кружками. 6. Поставити знаки в кожному проміжку, на якій числова вісь розбивається відміченими точками. Спочатку поставити знак у самому правому проміжку на числовій осі за правилом: знак «+» ставиться, якщо число множників виду 7. Вибираються проміжки, в яких стоїть знак «+», якщо нерівність, отримана в пункті 4 має вигляд: Приклад 1. Розв’язати методом інтервалів нерівність
Розв’язування:З нерівності
Далі замість нерівності (1) розв’язуємо рівняння
Наносимо відповідні точки на числову вісь (див. рисунок).
Розглядаємо кожний з утворених інтервалів окремо. 1. Підставляємо значення 2. Підставляючи в нерівність (1) значення 3. Підставляючи в (3) значення Остаточно маємо розв’язок нерівності (1) Відповідь Приклад 2. Розв’язати нерівність Розв’язування: Для знаходження коренів рівняння
Отже числа
1 2 3 x Відповідь:
|
|||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 129; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.33.107 (0.012 с.) |
 . У випадку нерівності
. У випадку нерівності  ця схема аналогічна.
ця схема аналогічна. .
.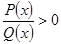 .
.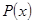 і
і  розкласти на множники. Якщо при цьому з’являються однакові множники, то треба замінити їх відповідним степенем. Наприклад,
розкласти на множники. Якщо при цьому з’являються однакові множники, то треба замінити їх відповідним степенем. Наприклад,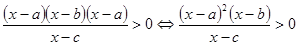 .
.

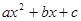 , де
, де 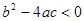 , то його виключення залежить від знака старшого коефіцієнта і виконується за правилом:
, то його виключення залежить від знака старшого коефіцієнта і виконується за правилом:
 , то його виключення здійснюється за правилами
, то його виключення здійснюється за правилами



 .
. парне, і знак «-», якщо це число непарне. Знаки в інших проміжках ставляться з урахуванням того, що вони чергуються в сусідніх проміжках.
парне, і знак «-», якщо це число непарне. Знаки в інших проміжках ставляться з урахуванням того, що вони чергуються в сусідніх проміжках. , або «-», якщо ця нерівність має вигляд
, або «-», якщо ця нерівність має вигляд  . Ці проміжки містять у собі крайні точки, відмічені на числовій осі зафарбованими кружками, і не містять точок, відмічених світлими кружками,. Об’єднання цих проміжків і є множиною розв’язків даної нерівності.[4:124]
. Ці проміжки містять у собі крайні точки, відмічені на числовій осі зафарбованими кружками, і не містять точок, відмічених світлими кружками,. Об’єднання цих проміжків і є множиною розв’язків даної нерівності.[4:124]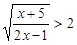 . (1)
. (1) знаходимо ОДЗ:
знаходимо ОДЗ: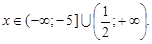
 або
або  звідки
звідки 
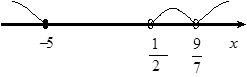
 з інтервалу
з інтервалу  у нерівність (1). Дістаємо нерівність
у нерівність (1). Дістаємо нерівність  , яка не виконується. Тому нерівність (1) не виконується в усіх точках інтервалу
, яка не виконується. Тому нерівність (1) не виконується в усіх точках інтервалу  з інтервалу
з інтервалу 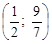 , дістаємо правильну нерівність
, дістаємо правильну нерівність 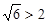 . Отже, нерівність (1) виконується на інтервалі
. Отже, нерівність (1) виконується на інтервалі  з інтервалу
з інтервалу  дістаємо неправильну нерівність
дістаємо неправильну нерівність  . Це означає, що нерівність (1) не виконується ні в одній точці інтервалу
. Це означає, що нерівність (1) не виконується ні в одній точці інтервалу 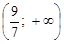 .
.
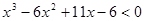

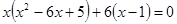
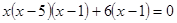



 ,
, 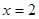 ,
,  є коренями даного рівняння. Наносимо ці числа на числову вісь і визначаємо знак лівої частини функції
є коренями даного рівняння. Наносимо ці числа на числову вісь і визначаємо знак лівої частини функції на одному з інтервалів. Зокрема, взявши точку
на одному з інтервалів. Зокрема, взявши точку  з інтервалу
з інтервалу 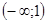 , дістаємо
, дістаємо 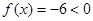 . Провівши «криву знаків», визначаємо знак
. Провівши «криву знаків», визначаємо знак  в кожному з інтервалів.
в кожному з інтервалів.



 +
+