Простой цикл, ограничивающий грань, назовём границей грани. Две грани будем называть соседними, если их границы имеют хотя бы одно общее ребро.

Лекция 2.

 Задача о полном графе, имеющем 5 вершин. Теорема Куратовского. Формула Эйлера для многогранников

 

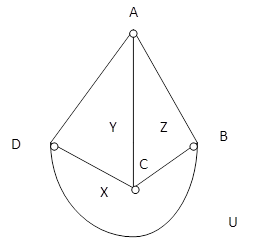
Задача о полном графе, имеющем 5 вершин.

 Доказать, что любой полный граф, имеющий пять вершин, неплоский.

Решение.

 Вершины графа обозначим буквами А, В, С, D. По 4 точкам А, В, С, D построим полный граф, он будет плоским и разделит плоскость на четыре области (рис. 1).

Рис. 1

Обозначим эти области буквами X,Y,Z,U. Тогда 5 вершина будет расположена в одной из этих областей. Но тогда полный граф, построенный на таких 5 вершинах, никак не может быть плоским. Проведя рассуждения, аналогичные предыдущим, получаем, что полный граф с пятью вершинами действительно плоским быть не может.  

    Полный граф с пятью вершинами (см. рис. 2) позволяют определить целое  семейство не планарных графов и играет особую роль в определении того, является ли данный граф планарным или нет.

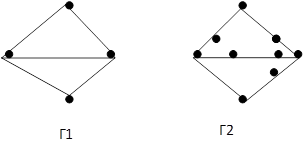
Рис. 2

Эти два графа, изображённые на рис. 2, называются графами Куратовского. Критерий, характеризующий плоские графы, был предложен в 1930 г. польским математиком Куратовским.

Чтобы сформулировать его, мы должны сначала объяснить, что нужно понимать под расширением и сжатием графа.

Расширение и сжатие графа

Предположим, что на некоторые рёбра графа мы поставили новые вершины, так что эти рёбра стали элементарными цепями, состоящими из нескольких рёбер. Эту операцию мы назовём расширением графа.

На рис. 3 приведён пример расширения, переводящего граф Г1, содержащий всего четыре вершины, в граф Г2.

Рис. 3

    Обратно, предположим, что мы имеем такой граф, как Г2, на рис. 3, содержащий элементарные цепи, разделённые на рёбра, причём из промежуточных вершин не исходит никаких других рёбер. Посредством обратной операции он может быть сжат в такой граф, на котором его элементарные цепи становятся рёбрами. Так, граф Г2 на рис. 3 может быть сжат в граф Г1 путём удаления вершин из соответствующих элементарных цепей, соединяющих их вершины. Теперь сформулируем теорему Куратовского.

Теорема Куратовского. Для того, чтобы граф был планарным, т.е., чтобы его можно было бы изобразить плоским графом, необходимо и достаточно, чтобы он не содержал внутри себя никакого графа, который можно было бы сжать до графов Куратовского (т.е. до пятиугольного графа Г5 или шестиугольного графа Г6).

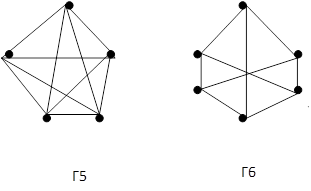
Рис. 4. Графы Куратовского

Заметим, что всякий плоский граф может быть изображён на поверхности сферы. Очевидно, что в этом случае такое изображение будет уже не плоским, а планарным графом. Существует много способов такого представления. Например, можно воспользоваться для этого стереографической проекцией, этот метод часто используется картографами, особенно для составления карт районов земного шара, лежащих вблизи полюсов.

 

Формула Эйлера для многогранников

 В качестве характеристики плоского представления графа вводится понятие грани.

 Гранью в плоском представлении графа называется часть плоскости, ограниченная простым циклом и не содержащая внутри других циклов.

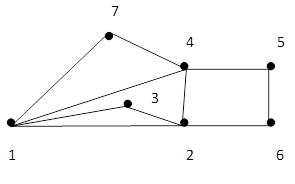
Рис. 5

На рис. 5 имеем плоское представление графа с четырьмя гранями: (1,7,4,1), (1,2,3,1), (1,3,2,4,1), (2,6,5,4,2). Часть плоскости, ограниченная простым циклом (1,2,4,1), гранью не является, так как содержит внутри себя цикл (1,2,3,1).

Лекция 2.

 Задача о полном графе, имеющем 5 вершин. Теорема Куратовского. Формула Эйлера для многогранников

 

Задача о полном графе, имеющем 5 вершин.

 Доказать, что любой полный граф, имеющий пять вершин, неплоский.

Решение.

 Вершины графа обозначим буквами А, В, С, D. По 4 точкам А, В, С, D построим полный граф, он будет плоским и разделит плоскость на четыре области (рис. 1).

Рис. 1

Обозначим эти области буквами X,Y,Z,U. Тогда 5 вершина будет расположена в одной из этих областей. Но тогда полный граф, построенный на таких 5 вершинах, никак не может быть плоским. Проведя рассуждения, аналогичные предыдущим, получаем, что полный граф с пятью вершинами действительно плоским быть не может.  

    Полный граф с пятью вершинами (см. рис. 2) позволяют определить целое  семейство не планарных графов и играет особую роль в определении того, является ли данный граф планарным или нет.

Рис. 2

Эти два графа, изображённые на рис. 2, называются графами Куратовского. Критерий, характеризующий плоские графы, был предложен в 1930 г. польским математиком Куратовским.

Чтобы сформулировать его, мы должны сначала объяснить, что нужно понимать под расширением и сжатием графа.

Расширение и сжатие графа

Предположим, что на некоторые рёбра графа мы поставили новые вершины, так что эти рёбра стали элементарными цепями, состоящими из нескольких рёбер. Эту операцию мы назовём расширением графа.

На рис. 3 приведён пример расширения, переводящего граф Г1, содержащий всего четыре вершины, в граф Г2.

Рис. 3

    Обратно, предположим, что мы имеем такой граф, как Г2, на рис. 3, содержащий элементарные цепи, разделённые на рёбра, причём из промежуточных вершин не исходит никаких других рёбер. Посредством обратной операции он может быть сжат в такой граф, на котором его элементарные цепи становятся рёбрами. Так, граф Г2 на рис. 3 может быть сжат в граф Г1 путём удаления вершин из соответствующих элементарных цепей, соединяющих их вершины. Теперь сформулируем теорему Куратовского.

Теорема Куратовского. Для того, чтобы граф был планарным, т.е., чтобы его можно было бы изобразить плоским графом, необходимо и достаточно, чтобы он не содержал внутри себя никакого графа, который можно было бы сжать до графов Куратовского (т.е. до пятиугольного графа Г5 или шестиугольного графа Г6).

Рис. 4. Графы Куратовского

Заметим, что всякий плоский граф может быть изображён на поверхности сферы. Очевидно, что в этом случае такое изображение будет уже не плоским, а планарным графом. Существует много способов такого представления. Например, можно воспользоваться для этого стереографической проекцией, этот метод часто используется картографами, особенно для составления карт районов земного шара, лежащих вблизи полюсов.

 

Формула Эйлера для многогранников

 В качестве характеристики плоского представления графа вводится понятие грани.

 Гранью в плоском представлении графа называется часть плоскости, ограниченная простым циклом и не содержащая внутри других циклов.

Рис. 5

На рис. 5 имеем плоское представление графа с четырьмя гранями: (1,7,4,1), (1,2,3,1), (1,3,2,4,1), (2,6,5,4,2). Часть плоскости, ограниченная простым циклом (1,2,4,1), гранью не является, так как содержит внутри себя цикл (1,2,3,1).

Простой цикл, ограничивающий грань, назовём границей грани. Две грани будем называть соседними, если их границы имеют хотя бы одно общее ребро.

Бесконечная грань.  В качестве грани можно рассматривать и часть плоскости, расположенную "вне" плоского представления графа; она ограничена "изнутри" простым циклом и не содержит в себе других циклов. Эту часть плоскости называют "бесконечной" гранью.