
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ускоренный градиент Нестерова
Однако шар, который катится вниз по склону, слепо следуя искривлениям склона, крайне неудовлетворителен. Хотелось бы иметь более умный шар, который имеет представление о том, куда он движется, чтобы он знал, что нужно замедляться, прежде чем холм снова поднимется. Ускоренный градиент Нестерова (NAG) [6] – это способ придать нашему коэффициенту импульса (momentum term) предвидение такого рода. Мы знаем, что будем использовать коэффициент импульса γ v t−1 для перемещения параметров θ. Тогда вычисление θ − γ v t−1 даёт аппроксимацию следующей позиции параметров (при отсутствии градиента для полного обновления), грубое представление о том, где будут находиться наши параметры. Теперь можем эффективно смотреть в будущее, вычисляя градиент не относительно текущих параметров θ, а относительно приблизительного будущего положения о параметрах: θ` = θ – γ v t–1 (место, ближе к точке, где окажемся на след.шаге) v t = γ v t-1 + η ∇ θ J(θ`) (скорость для перемещения на тек.шаге) θ = θ – v t. (найдём следующую позицию) Опять же, устанавливаем коэффициент импульса γ в значение около 0.9. В то время как импульс сначала вычисляет текущий градиент (маленький синий вектор на рис.4), а затем делает большой скачок в направлении обновлённого накопленного градиента (большой синий вектор), NAG сначала делает большой скачок в направлении предыдущего накопленного градиента (коричневый вектор), измеряет градиент, а затем вносит поправку (красный вектор), что приводит к полному NAG- обновлению (зеленый вектор). Это упреждающее обновление не позволяет идти слишком быстро и приводит к улучшению чувствительности, что значительно повышает производительность RNN для ряда задач [7].
Рис.4: Обновление Нестерова (исходник: лекция 6c G. Hinton)
Для получения другого объяснения интуитивной идеи, стоящей за NAG, обраться можно сюда, в то время как Ilya Sutskever даёт более подробный обзор в своей докторской диссертации [8]. Импульс Нестерова – набирающая популярность версия обновления импульса, что обладает более сильными теоретическими гарантиями сходимости для выпуклых функций, и на практике также работает немного лучше, чем стандартный импульс.
Основная идея импульса Нестерова в том, что когда текущие параметры находится в некоторой позиции x, то глядя на обновление импульса выше, известно, что одно только слагаемое импульса (т.е. игнорируем 2е слагаемое с градиентом) собирается подтолкнуть параметры на γ v t−1. Поэтому, чтобы вычислить градиент можно рассматривать «перспективу» – будущую приблизительную позицию x + γ v t−1, точку в окрестности, которой скоро окажемся. Следовательно, имеет смысл вычислять градиент в точке x + γ v t−1, а не в «старой/устаревшей» позиции x. Теперь, адаптировав обновления к наклону функции ошибок, и ускорив SGD, в свою очередь, хотелось бы адаптировать обновления каждого отдельного параметра для выполнения больших или меньших обновлений в зависимости от их важности.
Adagrad Adagrad [9] – это алгоритм оптимизации на основе градиента, который делает именно это: он а даптирует скорость обучения по параметрам, выполняя небольшие обновления(т.е. низкая скорость обучения) для параметров, связанных с часто встречающимися признаками, и более крупные обновления (т.е. высокая скорость обучения) для параметров, связанных с редкими признаками. По этой причине он хорошо подходит для работы с разрежёнными данными. Dean et al. [10] обнаружили, что Adagrad улучшил надёжность/устойчивость SGD значительно, и использовали его для обучения крупномасштабных нейронных сетей в Google, которые среди прочего научились распознавать кошек в видео на Youtube. Более того, Pennington et al. [11] использовали Adagrad для обучения встраивания слов (word embedding) GloVe, т.к. редкие слова требуют гораздо больших величин обновления, чем часто встречающиеся. Ранее мы выполняли обновление всех параметров θ одновременно, поскольку каждый параметр θi использовал одинаковую скорость обучения η. Поскольку Adagrad может использовать различную скорость обучения для каждого параметра θi на каждом шаге t, то вначале покажем Adagrad- обновление каждого параметра, затем его векторизуем. Для краткости используем gt для обозначения градиента на шаге времени t.
gt, i = ∇θ J(θ t, i) Обновление SGD для каждого параметра θi на каждом шаге t становится: θ t +1, i = θ t , i – η ⋅ gt , i В правиле обновления Adagrad изменяет общую скорость обучения η на каждом шаге t для каждого параметра θi на основе прошлых градиентов, которые были вычислены для θi:
здесь Gt ∈ Rd × d – диагональная матрица, где каждый диагональный элемент i,i является суммой квадратов градиентов относительно θ i до временного шага t [12], а ϵ является сглаживающим слагаемым, которое позволяет избежать деления на 0 (обычно порядка 10−8). Интересно, что без операции квадратного корня алгоритм работает намного хуже. Поскольку Gt содержит сумму квадратов прошлых градиентов по всем параметрам θ вдоль своей диагонали, можно векторизовать реализацию, выполнив произведение ⊙ матрицы Gt на вектор gt:
Одним из главных преимуществ Adagrad является то, что он устраняет необходимость ручной настройки скорости обучения. Большинство реализаций используют значение по умолчанию 0.01 и оставляют его таким. Главная слабость Adagrad – это накопление квадратов градиентов в знаменателе: поскольку каждый добавленный член является положительным, накопленная сумма продолжает расти в процессе обучения. Что, в свою очередь, приводит к уменьшению скорости обучения, которая в конечном итоге становится бесконечно малой, в этот момент алгоритм больше не может получать дополнительные знания. Следующие алгоритмы направлены на устранение этого недостатка.
Adadelta Алгоритм Adadelta [13] является продолжением Adagrad, который стремится сократить агрессивное монотонное уменьшение скорости обучения. Вместо того, чтобы накапливать все квадраты градиентов прошлого, Adadelta ограничивает окно накопления градиентов прошлого некоторым фиксированным размером w. Вместо неэффективного хранения w штук предыдущих квадратов градиентов, сумма рекурсивно определяется как затухающее среднее (decaying average) всех прошлых квадратов градиентов. Скользящее среднее E[g2]t (running average) на шаге времени t зависит (аналогично, как множитель γ для коэффициента импульса) только от предыдущего среднего и текущего градиента: E[g2]t = γ E[g2]t–1 + (1- γ) gt2 Устанавливаем значение γ, аналогичное коэффициенту импульса, около 0.9. Для ясности, теперь перепишем известное SGD -обновление в терминах обновления вектора параметров Δθt: Δθ t = – η ⋅ gt,i θ t+1 = θ t + Δθ t Тогда Adagrad -обновление параметров, полученное ранее, имеет вид:
Теперь можно заменить диагональную матрицу Gt на затухающее среднее E[g2]t нескольких последних квадратов градиентов:
Поскольку знаменатель – это просто критерий среднеквадратичной ошибки (RMS) градиента, можно заменить критерий его обозначением: Δθ t = –η / (RMS [ g ] t) ⊙ gt Отметим, что единицы измерения в этом обновлении (как и в SGD, импульсе или Adagrad) не совпадают, т.е. обновление должно иметь те же гипотетические единицы, что и параметр. Чтобы реализовать это, сначала нужно определить другое экспоненциально затухающее среднее, на этот раз не квадратов градиентов, а квадратов обновлений параметров: Е[Δθ2] t = γ Е[Δθ2] t –1 + (1–γ) Δθt2 Среднеквадратическая ошибка обновления параметров таким образом:
Поскольку RMS[Δθ]t неизвестна, приближаемся к ней через RMS обновления параметров до предыдущего временного шага. Замена скорости обучения η в предыдущем правиле обновления на RMS[Δθ]t−1, наконец, даёт правило обновления Adadelta:
θ t +1 = θ t + Δθt Используя Adadelta, даже не нужно устанавливать скорость обучения по умолчанию, т.к. она была исключена из правила обновления.
RMSprop RMSprop – это неопубликованный метод адаптивной скорости обучения, предложенный Geoff Hinton на 6й лекции его курса на Coursera. RMSprop и Adadelta разработаны независимо друг от друга в одно и то же время, связаны необходимостью разрешения уменьшающейся скорости обучения по порядку квадратного корня, взятого у Adagrad. RMSprop фактически идентичен 1му вектору обновления Adadelta, который был получен выше:
RMSprop также делит скорость обучения на экспоненциально затухающее среднее квадратов градиентов. Hinton предлагает установить γ равным 0.9, тогда как хорошее значение по умолчанию для скорости обучения η составляет 0.001.
Adam Адаптивная Оценка Импульсов (Adam – Adaptive Moment) [14] – это ещё 1 метод, который вычисляет адаптивные скорости обучения для каждого параметра. В дополнение к хранению экспоненциально затухающего среднего последних квадратов градиентов v t, как Adadelta и RMSprop, Adam также сохраняет экспоненциально затухающее среднее последних градиентов mt, аналогично импульсу. В то время как импульс можно рассматривать как шар, бегущий по склону, Adam ведет себя как тяжелый шар с трением, который, таким образом, предпочитает плоские минимумы на поверхности ошибки [15]. Мы вычисляем средние значения затухания прошлых и прошлых квадратов градиентов mtmt и vtvt соответственно следующим образом: mt = β1 mt–1 + (1–β1) gt (затухающее среднее градиентов) v t = β2 v t–1 + (1–β2) g t 2 (затухающее среднее квадратов градиентов) mt и v t являются оценками первого статического момента (среднего значения – m ean) и второго момента инерции (нецентрированной дисперсии – uncentered v ariance) градиентов соответственно, отсюда и название метода. Поскольку mt и v t инициализируются как векторы нулей, авторы Adam отмечают, что они смещены к 0, особенно на начальных шагах, и особенно, когда скорости затухания (decay rates) малы (т.е. β1 и β2 близки к 1). Авторы противодействуют этим отклонениям, вычисляя скорректированные смещением оценки первого и второго моментов:
Затем эти оценки используются для обновления параметров, как в Adadelta и RMSprop, что приводит к правилу обновления Adam:
Предлагаются значения по умолчанию: β1=0.9, β2=0.999 и ϵ=10-8. Авторы эмпирически показывают, что Adam хорошо работает на практике и выгодно отличается от других методов адаптивного обучения.
AdaMax Коэффициент v t в правиле обновления Adam масштабирует градиент обратно пропорционально L 2 норме прошлых градиентов (исп. v t−1) и текущему градиенту |gt|2: v t = β2 v t−1 + (1–β2) |gt|2 Можно обобщить это обновление до нормы L p. Отметьте, что Kingma and Ba также параметризуют и β2, как β2 p: v t = β2 p v t–1 + (1- β2 p) |gt| p Нормы для больших значений p обычно становятся численно нестабильными, поэтому нормы L 1 и L 2 наиболее распространены на практике. Однако норма L ∞ также обычно демонстрирует устойчивое поведение. По этой причине авторы предлагают AdaMax (Kingma and va, 2015) и показывают, что v t с L ∞ сходится к следующему более стабильному значению. Чтобы избежать путаницы с Adam, используем ut для обозначения v t, ограниченного нормой бесконечности: ut = β2∞ v t–1 + (1–β2∞) |gt|∞ = max(β2 v t–1, |gt|) Теперь можно вставить это в уравнение обновления Adam, заменив
Обратите внимание, поскольку ut полагает операцию max, он не так подвержен к смещению в сторону 0, как mt и v t в Adam, поэтому не нужно вычислять поправку смещения для ut. Хорошими значениями по умолчанию являются η=0.002, β1=0.9 и β2=0.999.
Nadam Ранее указано, что A dam можно рассматривать как комбинацию RMSprop и импульса: RMSprop вносит экспоненциально затухающее среднее прошлых квадратов градиентов v t, в то время как импульс учитывает экспоненциально убывающее среднее прошлых градиентов mt. Ускоренный градиент Нестерова (NAG) превосходит обыкновенный метод импульса. Nadam (Nesterov-accelerated Adaptive Moment Estimation – Адаптивная Оценка Импульсов, ускоренная по Нестерову) [16], таким образом, объединяет A dam и NAG. Чтобы включить NAG в A dam, нужно изменить его коэффициент импульса mt. Давайте вспомним правило обновления импульса, используя текущую запись:
где J – целевая функция, γ – коэффициент затухания импульса, а η – размер шага. Разложение 3го уравнения выше даёт: θt +1 = θt – (γ mt –1 + η gt) Что ещё раз демонстрирует, что импульс включает в себя шаг в направлении предыдущего вектора импульса и шаг в направлении текущего градиента. Затем NAG позволяет выполнять более точный шаг в направлении градиента, обновляя параметры с шагом импульса перед вычислением градиента. Таким образом, нужно только изменить градиент gt, чтобы получить NAG:
Dozat предлагает изменить NAG следующим образом: вместо того, чтобы дважды применять шаг импульса – 1 раз для обновления градиента gt и 2й раз для обновления параметров θt +1 – теперь напрямую применяем опережающий импульс обновить текущие параметры:
Отметьте, что вместо предыдущего импульса mt −1, как в уравнении расширенногоправила обновления импульса выше, теперь используется текущий импульс mt, для того чтобы заглянуть в будущее. Таким образом, чтобы добавить импульс Нестерова к A da m, можно аналогичным образом заменить предыдущий импульс текущим импульсом.
Напомним, что правило обновления A da m следующее (обратите внимание, что изменять
Расширение 2го уравнения с определениями
Обратите внимание, что
есть просто уточнённая-по-смещению (bias-corrected) оценка вектора импульса предыдущего шага времени. Таким образом, можно заменить её на
То, что знаменатель равен 1– β 1 t, а не 1– β 1 t -1, игнорируется для простоты, т.к. всё равно знаменатель будет заменён на следующем шаге. Это уравнение снова выглядит очень похоже на расширенное правило обновления импульса выше. Теперь можно добавить импульс Нестерова, как было сделано ранее, просто заменив эту уточнённую-по-смещению оценку импульса предыдущего временного шага
AMSGrad Поскольку адаптивные методы обучения стали нормой при обучении нейронных сетей, на практике было замечено, что в некоторых случаях, например, для распознавания объектов [17] или машинного перевода [18] эти методы не сходятся к оптимальному решению и их опережает SGD с импульсом. Reddi et al. (2018) [19] формализуют эту проблему и указывают экспоненциальное скользящее среднее (exponential moving average) последних квадратов градиентов как причину плохого обобщающего поведения методов адаптивной скорости обучения. Напомним, что введение экспоненциального среднего было хорошо мотивировано: оно должно предотвратить бесконечно малые скорости обучения в процессе обучения, что является ключевым недостатком алгоритма Adagrad. Однако это кратковременное запоминание градиентов становится препятствием в других сценариях. В условиях, когда Ada m сходится к неоптимальному решению, было замечено, что некоторые мини-пакеты предоставляют большие и информативные градиенты, но, поскольку эт и мини-пакеты встречаются редко, экспоненциальное среднее уменьшает их влияние, что приводит к плохой сходимости. Авторы приводят пример простой выпуклой задачи оптимизации, где такое же поведение можно наблюдать для Ada m. Чтобы исправить это поведение, авторы предлагают новый алгоритм AMSGrad, который использует максимум прошлых квадратов градиентов v t, а не экспоненциальное среднее для обновления параметров. v t определяется так же, как в Ada m: v t = β 2 v t -1 + (1- β 2) gt 2 Вместо v t (или его уточнённой-по-смещению версии
Таким образом, AMSGrad приводит к увеличению размера шага, что позволяет избежать проблем, с которыми сталкивается Ada m. Для простоты авторы также удаляют этап (debiasing) коррекции смещения, присутствующий в Ada m. Полное обновление AMSGrad без исправленных смещений оценок показано ниже:
Авторы наблюдают улучшение производительности по сравнению с Ada m на небольших наборах данных и на CIFAR-10. Другие эксперименты, однако, показывают аналогичную или худшую производительность, чем Ada m. Ещё неизвестно, сможет ли AMSGrad последовательно превзойти Ada m на практике. Для получения дополнительной информации о последних достижениях в области оптимизации Deep Learning см. этот блог.
Визуализация алгоритмов Следующие 2 анимации (рис 5,6. предоставлены: Alec Radford) обеспечивают некоторые интуитивные предположения о поведении оптимизации большинства представленных методов. Также посмотрите здесь описание тех же изображений, сделанных Karpathy, другой краткий обзор обсуждаемых алгоритмов. На Рис.5 видно их поведение на контурах поверхности потерь (Beale function) с течением времени. Обратите внимание, что Adagrad, Adadelta и RMSprop почти сразу же движутся в правильном направлении и сходятся быстро, в то время как импульс и NAG выводятся из «колеи», изображая шар, катящийся вниз по склону. NAG, однако, быстро может скорректировать свой курс благодаря повышенной чувствительности, заглядывая в будущее при движении к минимуму. http://ruder.io/content/images/2016/09/contours_evaluation_optimizers.gif Рис.5: Оптимизация SGD на контурах поверхности потерь http://ruder.io/content/images/2016/09/saddle_point_evaluation_optimizers.gif Рис.6: Оптимизация SGD в седловой точке
На Рис.6 показано поведение алгоритмов в седловой точке, т.е. в точке, где одно измерение имеет положительный наклон, а другое измерение имеет отрицательный наклон, что создает трудности для SGD, как упоминали ранее. Отметьте, что SGD, импульс и NAG испытывают трудности с нарушением симметрии, хотя 2м последним в конечном итоге удаётся избежать седловой точки, в то время как Adagrad, RMSprop и Adadelta быстро снижают отрицательный уклон. Как можно видеть, методы адаптивной скорости обучения, т.е. Adagrad, Adadelta, RMSprop и Adam, являются наиболее подходящими и обеспечивают наилучшую сходимость для этих сценариев. Примечание: если Вы заинтересованы в визуализации этих или других алгоритмов оптимизации, обратитесь к этому полезному руководству.
|
|||||||||
|
Последнее изменение этой страницы: 2019-11-02; просмотров: 939; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.174.156 (0.108 с.) |











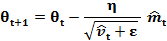
 на ut, чтобы получить правило обновления AdaMax:
на ut, чтобы получить правило обновления AdaMax:





 не нужно):
не нужно):
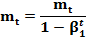

 и mt даёт:
и mt даёт:

 :
:








