
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разности решетчатых функций и разностные уравнения
Скорость изменения РФ характеризуется ее первой разностью или разностью первого порядка, являющейся аналогом первой производной для непрерывных функций.
Рисунок 1.4.1
Различают левые и правые разности:
Соотношение между РФ y [ n ] и ее разностями
Если в уравнении (1.4.4) разности РФ заменить соответствующими РФ из выражений (1.4.1,1.4.2), то получим следующую форму записи разностного уравнения:
Порядок разностного уравнения может не совпадать порядком наивысшей разности, обычно порядок уравнения определяется после приведения к виду (1.4.5). Если выражение содержит РФ вида y [ n ] и y [ n + K ], то оно имеет порядок К. Это положение иллюстрируется следующим примером:
Произведём замену
Дискретные системы во временной области описываются разностными уравнениями также, как непрерывные – дифференциальными. 1.5 Дискретное (D) преобразование Лапласа. Дискретное преобразование Лапласа является функциональным преобразованием РФ и определяется соотношением:
Если сравнить с преобразованием Лапласа непрерывных функций (1.5.2), то легко найти аналогию между ними.
Изображение F * (q, e) существует, если ряд (1.5.3) сходящийся. Значение Если РФ имеет ограниченный порядок роста, т.е.
Рассмотрим несколько примеров. Пример 1.

Рисунок 1.5.1
Сумма S бесконечно убывающей прогрессии имеет вид:
Пример 2.
При e=0, получим
Рассмотрим теперь Обычно выбирают такую полосу симметрично относительно оси абсцисс -π < Im q <π (рисунок 1.5.2).
Рисунок 1.5.2
1.6 Основные теоремы, правила D-преобразования 1. Свойство линейности. Изображение линейной комбинации РФ соответствует линейной комбинации их изображений.
2. Теорема смещения оригиналов в области независимого переменного (теорема сдвига). Смещение независимого переменного на величину ±k соответствует в области изображений умножению на
при условии 3. Изображение разности. Операция взятия «к -ой» разности в области оригинала, в области изображения соответствует умножение на сомножитель
при нулевых начальных условиях. 4. Изображение суммы. Суммирование в области оригинала соответствует в области изображений делению на
5. Теорема свертывания в вещественной области или умножение изображений. Произведению изображений соответствует в области оригиналов сумма:
6. Теорема о конечном значении РФ
Прямое D преобразование:
Обратное D преобразование:
1.7 Z преобразование Родственное D – преобразованию, получаемое заменой
Рисунок 1.7.1
Особый отрезок L на плоскости q отображается на плоскости Z в окружность радиуса r.
Рисунок 1.7.2
|
||||||||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.25.32 (0.009 с.) |


 (1.4.3)
(1.4.3) Пример:
Пример: 


 называется разностным уравнением или уравнением в конечных разностях.
называется разностным уравнением или уравнением в конечных разностях. (1.4.4)
(1.4.4) (1.4.5)
(1.4.5)
 . В результате получили разностное уравнение первого порядка:
. В результате получили разностное уравнение первого порядка:
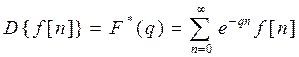 (1.5.1)
(1.5.1)
 , при котором
, при котором  – ряд сходится, а при
– ряд сходится, а при  – расходится, называется абсциссой сходимости. Если для данной РФ f [ n ] абсцисса сходимости
– расходится, называется абсциссой сходимости. Если для данной РФ f [ n ] абсцисса сходимости  , то ряд (1.5.1 или 1.5.3) сходится при всех значениях q, удовлетворяющих условию Re q > σc. В этом случае РФ называется преобразуемой.
, то ряд (1.5.1 или 1.5.3) сходится при всех значениях q, удовлетворяющих условию Re q > σc. В этом случае РФ называется преобразуемой. – то изображение РФ существует.
– то изображение РФ существует.
 (1.5.4)
(1.5.4) a1 - первый член геометрической прогрессии, d - знаменатель прогрессии (отношение последующего члена прогрессии к предыдущему).
a1 - первый член геометрической прогрессии, d - знаменатель прогрессии (отношение последующего члена прогрессии к предыдущему).
 (1.5.7)
(1.5.7) на плоскости комплексного переменного q. Так как
на плоскости комплексного переменного q. Так как  , а
, а  вдоль мнимой оси на плоскости комплексной переменной q, то F * (q), также является периодической функцией
вдоль мнимой оси на плоскости комплексной переменной q, то F * (q), также является периодической функцией  вдоль мнимой оси плоскости q и полностью определяется при
вдоль мнимой оси плоскости q и полностью определяется при  в любой полосе шириной 2π параллельной оси абсцисс.
в любой полосе шириной 2π параллельной оси абсцисс.
 (1.6.1)
(1.6.1) .
. (1.6.2)
(1.6.2)
 при нулевых начальных условиях.
при нулевых начальных условиях. (1.6.3)
(1.6.3) .
. (1.6.4)
(1.6.4) (1.6.5)
(1.6.5) (1.6.6)
(1.6.6)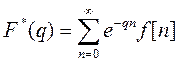 (1.6.7)
(1.6.7) (1.6.8)
(1.6.8)


 (рисунок 1.7.2)
(рисунок 1.7.2)



