
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближенное моделирование случайного процесса
3.1. Теоретические основания. Как отмечено в конце предыдущего параграфа, во многих случаях представляет интерес аппроксимация данного случайного процесса X t линейной моделью (5), т.е. конечной суммой:
Случайные коэффициенты Yk в (6) будем называть координатами случайного процесса Xt Выбор координат и системы детерминированных функций yk (t) неоднозначен и зависит от условий задачи, для решения которой используется аппроксимация (6). Вместе с тем известен достаточно общий подход к такому выбору, основанный на теореме разложения с.к. непрерывного случайного процесса в ряд со случайными ортогональными коэффициентами. Теорема 1. С.к. непрерывный вещественный гильбертов с.п. Xt, t Î [a,b], с M Xt º 0 и корреляционной функцией R(t,s) разлагается в ряд
сходящийся в среднем квадратическом при каждом t Î [a,b]. В этом разложении
с M Yk = 0, M YkYj = 0 при k¹ j и M
Доказательство этой теоремы можно найти в [2]. Формула (7) часто называется разложением Карунена-Лоэва. Замечание 1. Если Xt - гауссов процесс с M Xt º 0, то коэффициенты Yk ряда (7) являются независимыми гауссовыми величинами и ряд (7) сходится почти наверное при каждом t. Замечание 2. В случае гауссова процесса случайные коэффициенты в разложении (7) можно выбирать так, чтобы они были независимыми стандартными гауссовыми случайными величинами. Для этого новые коэффициенты ak следует положить равными
где Для приближенного моделирования произвольного процесса по формуле (6) достаточно смоделировать n -мерный вектор случайных коэффициентов (Y 1,..., Yn), координаты которого определены формулами (8). Использование формул (8) предполагает, что уже найдены собственные функции интегрального уравнения (9), хотя при решении этого уравнения можно столкнуться с серьезными трудностями. Но даже если все собственные функции уравнения (9) найдены, известны все конечномерные распределения процесса, но они не гауссовы, найти распределение даже отдельных коэффициентов Yk из формулы (8), вообще говоря, непросто. Тем более трудной представляется задача нахождения совместного распределения n коэффициентов для достаточно больших n. Эти обстоятельства и являются существенным препятствием к использованию формулы (6) для моделирования с.п. Xt. Если всё же предположить, что мы имеем совместное распределение коэффициентов Y 1,..., Yn для любого n и, следовательно, в принципе можем смоделировать вектор коэффициентов, то это означает лишь, что мы моделируем аппроксимирующую частную сумму ряда, в который разлагается процесс Xt. При этом сама аппроксимация процесса Xt n -й частной суммой ряда (7) вносит среднюю квадратическую погрешность величины
3.2. Приближенное моделирование винеровского процесса. Рассмотрим винеровский процесс w t на отрезке [0,1]. Для него w 0 = 0, M wt º 0 и R (t, s) = min (t, s). Собственные числа и собственные функции ядра R (t, s) легко находятся (см., например, [2]):
Так как винеровский процесс является гауссовым, то, учитывая замечание 2, для него запишем разложение в ряд:
где { ak, k = 0,1,...} - последовательность независимых гауссовых величин с параметрами (0,1). При фиксированном t этот ряд сходится с вероятностью 1. Для приближенного моделирования винеровского процесса при допустимой (заданной) с.к. погрешности e > 0 следует моделировать n -ю частную сумму ряда (12), выбирая n из условия
При выбранном n остается смоделировать n + 1 независимых гауссовых величин a 0, a 1,..., an и подставить их в n -ю частную сумму ряда (12). Таким образом, будем иметь приближенное равенство
с.к. погрешность которого не превосходит заданного e Замечание 3. Можно получить (см. [2]) несколько иное разложение wt, t Î [0,1] в ряд:
где ak, k = 0, 1,... - снова последовательность независимых гауссовых с.в. с параметрами (0,1). В этом случае при допустимой с.к. погрешности аппроксимации e следует выбирать n из условия
Тогда
|
||||||
|
Последнее изменение этой страницы: 2019-04-30; просмотров: 234; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.124.252 (0.007 с.) |
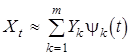 . (6)
. (6)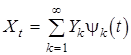 , (7)
, (7)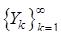 - ортогональная последовательность с.в., определяемых равенствами
- ортогональная последовательность с.в., определяемых равенствами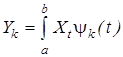 , k = 1, 2,... (8)
, k = 1, 2,... (8)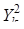 = D Yk = lk; lk > 0, yk(t) - соответственно собственные числа и собственные функции интегрального уравнения Фредгольма 2-го рода с ядром R(t,s):
= D Yk = lk; lk > 0, yk(t) - соответственно собственные числа и собственные функции интегрального уравнения Фредгольма 2-го рода с ядром R(t,s):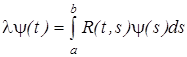 . (9)
. (9)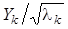 и тогда разложение процесса Xt в ряд будет иметь вид
и тогда разложение процесса Xt в ряд будет иметь вид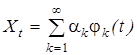 , (10)
, (10)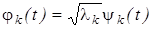 , а
, а 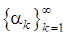 - последовательность независимых одинаково распределенных по закону N(0,1) случайных величин. Последнее обстоятельство, очевидно, существенно упрощает моделирование коэффициентов разложения, а следовательно, и самого процесса.
- последовательность независимых одинаково распределенных по закону N(0,1) случайных величин. Последнее обстоятельство, очевидно, существенно упрощает моделирование коэффициентов разложения, а следовательно, и самого процесса.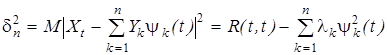 . (11)
. (11)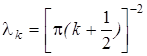 ,
, 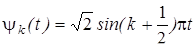 , k =0, 1,....
, k =0, 1,....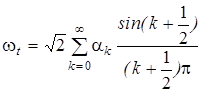 , (12)
, (12)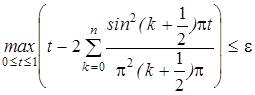 . (13)
. (13)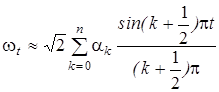 , (14)
, (14)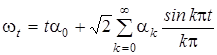 , (15)
, (15)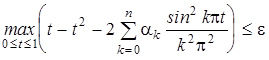 . (16)
. (16)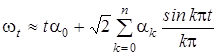 (17)
(17)


