
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Білет 20. Різні види рівнянь прямої ⇐ ПредыдущаяСтр 2 из 2
y=y +nt. Рівняння прямої у відрізках на осях має вигляд: Білет 21. Гіпербола. Гіперболою називають множину точок площини, абсолютна величина різниці відстаней яких до двох даних точок, що називаються фокусами, є величина стала ( Якщо дійсна і уявна вісь гіперболи рівні (тобто Рівняння гіперболи, фокуси якої лежать на осі Оу, має вигляд: а рівняння її асимптот:
Білет 22. Загальне рівняння площини.Рівняння площини,що проходять через три точки. Будь-яку площину можна задати рівнянням площини першого ступеня вигляду A x + B y + C z +D= 0, де A, B і C не можуть одночасно дорівнювати нулю. Якщо відомі координати трьох точок, через які проходить площину, то запишіть рівняння площини у вигляді визначника третього порядку. Нехай (х1, х2, х3), (у1, у2, у3) і (z1, z2, z3) - координати першої, другої і третьої точки відповідно. Тоді рівняння площини, що проходить через ці три точки, виглядає наступним чином: │x-x1y-y1z-z1│
Білет 23. Парабола.
Параболою називають множину точок на площині, рівновіддалених від даної точки, яку називають фокусом, і від даної прямої, яку називають директрисою.Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь Ох і вітки напрямлені вправо, має вигляд: Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь О і вітки напрямлені вліво, має вигляд:
Білет 24. Пряма в просторі.Кут між прямою і площиною. Канонічне рівняння прямої Рівняння прямої, що проходить через дві задані точки
Параметричні рівняння прямої
Кут між прямою і площино.:
Білет 25. Умова перпендикулярності і паралельності 2-х прямих. Умова перпендикулярності двох прямих: a) А1А2+В1В2=0; b) k2=-1/k1; Умова паралельності двох прямих: а) А1/А2=В1/В2; б) k1=k2.
Білет 26. Умова паралельності і перпендикулярності прямої і площини. Умова паралельності прямої і площини: mA+nB+lC=0. Умова перпендикулярності прямої і площини: A/m=B/n=C/l.
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 707; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.120.120 (0.007 с.) |
 Пряма на площині може бути задана у вигляді канонічного, параметричного або загального рівняння. Рівняння Ах+Ву+С=О за умови, що А і В одночасно не дорівнюють нулю, називається загальним рівнянням прямої. Для канонічного задання прямої потрібна точка прямої M0(х0,у0,t0), вектор
Пряма на площині може бути задана у вигляді канонічного, параметричного або загального рівняння. Рівняння Ах+Ву+С=О за умови, що А і В одночасно не дорівнюють нулю, називається загальним рівнянням прямої. Для канонічного задання прямої потрібна точка прямої M0(х0,у0,t0), вектор  =(m,n)-колінеарний прямій, тоді
=(m,n)-колінеарний прямій, тоді  -канонічне рівняння прямої. Якщо в рівняні (1) кожне з відношень позначити через t, то отримаємо параметричне рівняння прямої: x=x +mt
-канонічне рівняння прямої. Якщо в рівняні (1) кожне з відношень позначити через t, то отримаємо параметричне рівняння прямої: x=x +mt де a і b - відповідно абсциса і ордината точок перетину прямої з осями Ох і Оу. Рівняння прямої, яка проходить через дану точку А(ха,уа) в заданому напрямі, має вигляд у-уа =k(х-ха), де k=tqα - кутовий коефіцієнт прямої. Якщо пряма проходить через дві точки А (ха,уа) і В(хb, уb), то k=
де a і b - відповідно абсциса і ордината точок перетину прямої з осями Ох і Оу. Рівняння прямої, яка проходить через дану точку А(ха,уа) в заданому напрямі, має вигляд у-уа =k(х-ха), де k=tqα - кутовий коефіцієнт прямої. Якщо пряма проходить через дві точки А (ха,уа) і В(хb, уb), то k= 
 ), менша за відстань між фокусами (
), менша за відстань між фокусами ( ).Рівняння гіперболи, фокуси якої лежать на осі Ох, має вигляд:
).Рівняння гіперболи, фокуси якої лежать на осі Ох, має вигляд:  де
де  - довжина дійсної півосі;
- довжина дійсної півосі; 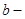 довжина уявної півосі. Залежність між параметрами
довжина уявної півосі. Залежність між параметрами  виражається співвідношенням:
виражається співвідношенням:  (11).Ексцентриситетом гіперболи називається відношення фокусної відстані
(11).Ексцентриситетом гіперболи називається відношення фокусної відстані  до її дійсої осі
до її дійсої осі 
 Гіпербола має дві асимптоти, рівняння яких
Гіпербола має дві асимптоти, рівняння яких  .
. ), то гіпербола називається рівносторонньою.
), то гіпербола називається рівносторонньою.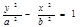 або
або  (16),
(16), (17).Гіперболи (10) і (16) називаються спряженими. Рівняння рівносторонньої гіперболи на осі Оу має вигляд:
(17).Гіперболи (10) і (16) називаються спряженими. Рівняння рівносторонньої гіперболи на осі Оу має вигляд:  .
.
 ), де
), де  -параметр параболи і відстань від фокуса до директриси. Рівняння її директриси
-параметр параболи і відстань від фокуса до директриси. Рівняння її директриси  .
. (19), де
(19), де  .Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь Оу і вітки напрямлені вгору, має вигляд:
.Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь Оу і вітки напрямлені вгору, має вигляд:  (20), де
(20), де  -параметр параболи і відстань від фокуса до директриси. Рівняння її директриси
-параметр параболи і відстань від фокуса до директриси. Рівняння її директриси  . Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь Оу і вітки напрямлені вгору, має вигляд:
. Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь Оу і вітки напрямлені вгору, має вигляд:  (20), де
(20), де 

 – називається канонічним рівнянням прямої, яка проходить через точку
– називається канонічним рівнянням прямої, яка проходить через точку  паралельно до вектора
паралельно до вектора  , який називається напрямним.
, який називається напрямним. – рівняння прямої, що проходить через дві задані точки
– рівняння прямої, що проходить через дві задані точки  і
і  . Це різновид канонічного рівняння прямої, коли
. Це різновид канонічного рівняння прямої, коли  , а
, а  .
. — параметричні рівняння прямої, де параметр
— параметричні рівняння прямої, де параметр  . Ці рівняння одержують із канонічного рівняння прямої.
. Ці рівняння одержують із канонічного рівняння прямої. — визначає рівняння прямої як лінію перетину двох непаралельних площин.
— визначає рівняння прямої як лінію перетину двох непаралельних площин. =
= 



