
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геом. и экон. приложения опр. интеграла. S плоской фигуры. Объем тела вращения ⇐ ПредыдущаяСтр 3 из 3
y=f(x) (f(x)≥0), то площадь криволинейной трапеции, ограниченной этой кривой, двумя прямыми x=a и x=b и отрезком оси абсцисс a≤x≤b, определяется формулой
Объём тела вращения криволин. трапеции, ограниченной кривой y= f(x), осью Ох и двумя прямыми x=a и x=b, вокруг оси Ох
Объём тела, образов. вращением вокруг оси Oy фигуры, огранич. кривой x=g(y), осью Oy и двумя прямыми y=c и y=d, Длина дуги гладкой кривой y=f(x) между двумя точками с абсциссами x=a и x=b
Средняя производительность труда, средняя мощность и др. вычисляется по формуле
Несобственные интегралы с бесконечными пределами интегрирования. Пусть функция y=f(x) определена на бесконечном промежутке Несобственным интегралом Если lim сущ и конечен, то несобств. интеграл Несобственный интеграл на бесконечном промежутке
Пусть функция y=f(x) определена для всех х. Несобственным интегралом с двумя бесконечными пределами интегрирования
Дифф-е ур-я. Соотношение вида Задача Коши:
№29.Диф уравнения 1-го порядка с разделяющимися переменными и приводящиеся к ним. Уравнение вида y´=f(x)g(y)-уравнение с разделяющимися переменными, m1(x)n1(y)dx+m2(x)n2(y)dy=0 -уравнение с разделяющимися переменными в симметричной форме. Основной метод решения- разделение переменных, т.е. умножение левой и правой частей уравнения на такой множитель, чтобы после упрощения при dx стояла функция только от х,при dy- только от y.
Проинтегрируем. Общий интеграл уравнений запишется в виде:
При умножении можно потерять соответственно решение y=y0, где g(y0)=0, для первого уравнения, или x=x0, где m2(x0)=0, и y=y0, где n1(y0)=0, для второго. Эти случаи следует рассматривать отдельно. Найти yk, такие, что g(yk)=0, и проверить являются ли y=yk решениями уравнения и заключены ли они в общем интеграле при каком-то значении Сk;аналогично для второго уравнения. Уравнение вида y´=f(ax+by+c) приводится к уравнению с разделяющимися переменными. ax+by+c=z(x) z´=a+by´; z´=a-+bf(z); dz/dx=a+bf(z).
№30 Однородные диф. уравнения 1-ого порядка. dy/dx = f (y/x) – однородное уравнение 1-го порядка Функция n переменных z = f (x1, x2,…,xn) называется однородной функцией степени
если №31. Линейные дифференциальные уравнения первого порядка. Методы решения. Линейное диф уравнение перв порядка - ур первой степени относительно у и у', т.е. ур вида у'+P(x)y=Q(x) (если Q(x)≡0, то уравнение однородное, если не равно то неоднородное) -Решение однородного уравнения
Общее решение: -Реш неоднородного ур: 1 метод Бернулли. искомая функция представляется в виде произведения двух функций
можно одну из составляющих произведение функций выбрать так, что выражение возможно получить функцию u, проинтегрировав, полученное соотношение как однородное диф уравнение. Для нахождения второй неизвестной функции v подставим поученное выражение для функции u в исходное уравнение
Окончательно получаем формулу:
|
|||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 140; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.27.244 (0.009 с.) |
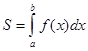

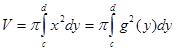




 - среднее значение функции.
- среднее значение функции. (т. е. на отрезке
(т. е. на отрезке  для любого А>a).
для любого А>a). от функции f(x) на бесконечном промежутке
от функции f(x) на бесконечном промежутке  называют предел
называют предел  .
. определяется аналогично.
определяется аналогично.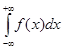 называется предел
называется предел  , если он существует и конечен.
, если он существует и конечен. +
+  наз-ся обыкновенным ДУ n-го порядка, если в F явно входит
наз-ся обыкновенным ДУ n-го порядка, если в F явно входит  (старшая производная) и не входят производные
(старшая производная) и не входят производные 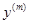 , где m>n. n определяет порядок ур-я. y’=f(x,y) – ур-е 1-го порядка. Если ф-я определена в
, где m>n. n определяет порядок ур-я. y’=f(x,y) – ур-е 1-го порядка. Если ф-я определена в  ,тоy=y(x) будет наз-ся решением ур-я
,тоy=y(x) будет наз-ся решением ур-я  (ур-е n-го порядка разрешенное относительно старшей производной) на
(ур-е n-го порядка разрешенное относительно старшей производной) на 
 нужно выделить реш-е, кот-е удовл. нач. условию (знак системы)
нужно выделить реш-е, кот-е удовл. нач. условию (знак системы) 


 ,
, 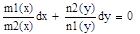
 ;
;  .
. , если формальная подстановка tx1 вместо x1, tx2 вместо х2,…, txn вместо xn, где t – любое допустимое число, после преобразований приведет к тождеству
, если формальная подстановка tx1 вместо x1, tx2 вместо х2,…, txn вместо xn, где t – любое допустимое число, после преобразований приведет к тождеству




 .
. - дифференцирование по частям. Подставляя в исходное уравнение, получаем:
- дифференцирование по частям. Подставляя в исходное уравнение, получаем:


 с учетом того, что выражение, стоящее в скобках, равно нулю.
с учетом того, что выражение, стоящее в скобках, равно нулю. ;
; 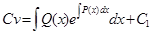 ;
;  ;
;



