Взаємне положення двох площин. Паралельність площин

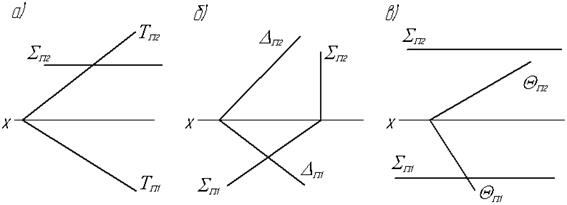
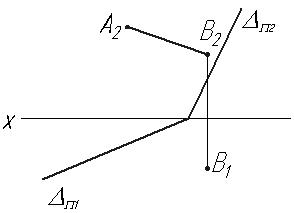
Основні положення:

· Дві площини паралельні, якщо дві пересічні прямі однієї площини паралельні, відповідно, двом пересічним прямим другої площини.

· У паралельних площин, які задані слідами, однойменні сліди паралельні.

Завдання 5.1 Через точку В провести площину паралельну заданій.

 

Задача 1 Задача 2

 

 

 

 

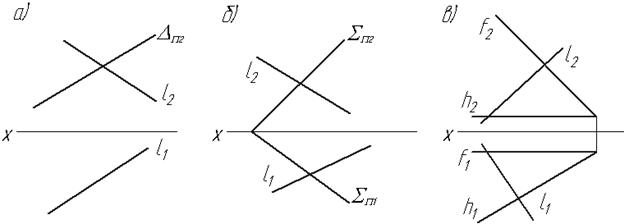
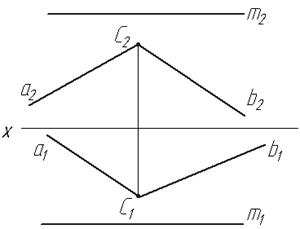
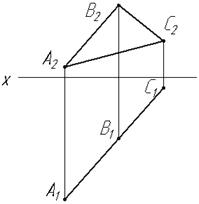
Перетин двох площин

Основні положення:

· Лінія перетину двох площин – пряма лінія. Вона проходить через дві точки, які є спільними для обох площин або через одну спільну точку, якщо відомий напрямок цієї лінії.

· Якщо обидві площини задано слідами, то лінія перетину визначається за точками перетину їх слідів.

· В загальному випадку для побудови лінії перетину двох площин використовують площини-посередники. За такі площини приймають площини рівня або проекцюючі площини.

Завдання 6.1 Побудувати проекції лінії перетину двох площин, які задані слідами.

Завдання 6.2 Побудуйте лінії перетину двох заданих площин (задачі а,б,в).

 

в)

 

 

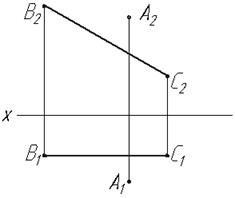
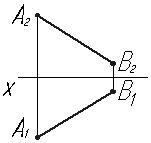
Паралельність та перпендикулярність прямої і площини. Перетин прямої та площини

Основні положення:

· Пряма і площина паралельні, якщо у площині можна провести пряму, яка б була паралельною заданій прямій.

· Пряма перпендикулярна площині, якщо вона перпендикулярна двом пересічним прямим, які належать цій площині.За такі пересічні прямі приймають головні лінії площини - горизонталь і фронталь.

· Дві площини взаємно перпендикулярні, якщо одна з них містить перпендикуляр до другої площини.

· Для побудови точки перетину прямої з площиною, необхідно:

1) через задану пряму провести допоміжну площину (проекцюючу);

2) знайти лінію перетину заданої та допоміжної площин;

3) на перетині прямих - заданої і одержаної - позначити шукану

точку.

· Відстань від точки до площини – це довжина перпендикуляра, який проведений через точку на задану площину.

 

Завдання 7.1 Побудувати відсутню проекцію відрізка АВ, паралельного заданій площині.

Завдання 7.2 Побудувати проекції площини, яка проходить через точку А та паралельна двом заданим прямим.

 

 

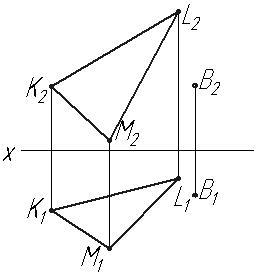
Завдання 7.3 Визначити точку перетину прямої з площиною. Визначити видимість елементів.

Завдання 7.4 Із точки Мпровести перпендикуляр до площини.

Завдання 7.5 Через пряму m провести площину перпендикулярну заданій площині.

 

 

Завдання 7.6 Визначити відстань від точки до площини.

Задача 1 Задача 2

 

 

 

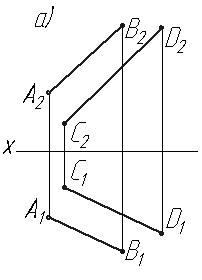
Розв’язання метричних та позиційних задач способами перетворення проекцій

Основні положення:

· Метод заміни площин проекцій:

положення точок, ліній, плоских фігур, поверхонь у просторі залишається незмінним, а замість існуючої площини проекцій обирають нову площину, що дозволяє об’єкт проекціювання перевести з загального положення в окреме (відносно нових площин проекцій).

· Плоско паралельнепереміщення:

- усі точки об’єкта переміщуються у площинах, які паралельні між собою та паралельні одній з площин проекцій;

- при переміщенні об’єкта відносно П₁ фронтальні проекції точок переміщуються паралельно до осі ОХ, а горизонтальна проекція,переміщуючись, не змінює свою форму та величину;

- при переміщенні об’єкта відносно П₂ горизонтальні проекції точок переміщуються паралельно до осі ОХ, а фронтальна проекція,переміщуючись, не змінює свою форму та величину;

· Обертання навколо осі, яка перпендикулярна до однієї з площин проекцій:

усі точки об’єкта на цій площині описують кола відповідних радіусів, а на іншій площині проекцій – переміщуються паралельно осі проекцій.

Завдання 8.1 Визначити кути нахилу відрізка АВ до площин П1 та П2 способом заміни площин проекцій.

Завдання 8.2 Визначити відстань від точки А до прямої ВС способом заміни площин проекцій.

 

Завдання 8.3 Визначити відстань між прямими способом плоско-паралельного переміщення.

 

 

Завдання 8.4 Визначити положення центру кола, описаного навколо трикутника. Використати спосіб обертання навколо проекціюючої осі

Завдання 8.5 Визначити основу перпендикуляра, проведеного з точки В до площини трикутника способом обертання навколо проекціюючої осі