
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основное уравнение кинетической теории газов. Основные газовые законы. Понятие температуры. Идеально-газовая шкала температур.Стр 1 из 12Следующая ⇒
Биноминальное распределение. Распределения Пуассона и Гаусса. Флуктуации. Бином Ньютона выражается формулой Распределение Пуассона: В случае n>>m и np=m0=const можно воспользоваться формулой Стирлинга Распределение Гаусса: Прологарифмируем распределение Пуассона, получим вблизи точки m=m0, ограничиваясь квадратичным членом, получим Флуктуация: мерой флуктуации является стандартное отклонение от среднего значения. Роль флуктуации возрастает с уменьшением области, в которой эти флуктуации рассматриваются. В макроскопических системах статических флуктуаций незначительны. Относительная роль флуктуации уменьшается с увеличением области и среднего числа частиц в ней.
7.Распределение молекул по скоростям. Распределение Максвелла по вектору скорости. Распределение Максвелла по компонентам скорости. получено при следующих условиях: все молекулы имеют одинаковую температуру (газ равновесный); при соударениях молекул соблюдается условие детального равновесия, т.е. при соударении пары молекул, когда эти молекулы поменяли свои скорости, в газе всегда найдутся две другие молекулы, которые приобрели те же самые скорости, которые имелись в первой паре до соударения, иначе, число молекул, имеющих заданную скорость не меняется со временем; все молекулы одинаковые (имеют одинаковую массу и размер). Максвелл предположил, что число молекул газа, имеющих скорости в диапазоне
коэффициента учтем, что абсолютному значению скорости имеет вид
Распределение Максвелла по абсолютному значению скорости. Характерные скорости. Распределение Максвелла по абсолютному значению скорости имеет вид
Характерные скорости Средняя арифметическая скорость Мы знаем среднюю квадратичную скорость. Вычислим среднюю арифметическую скорость по формуле
Нарисуем распределение Максвелла Распределение Максвелла
Наивероятнейшая скорость Видно, что распределение Максвелла имеет максимум. Найдем соответствующую этому максимуму скорость, которая называется наивероятнейшей скоростью. Используем условие обращения в нуль производной в соответствующей точке. Имеем
9.Приведенное распределение Максвелла. Число молекул в различных участках распределения Максвелла. Принцип детального равновесия. Приведенное распределение Введем переменную
Число молекул, имеющих скорости в заданном интервале Для нахождения числа молекул Δ N, имеющих скорости в диапазоне ϑ1<ϑ<ϑ2, следует найти интеграл
К сожалению, такой интеграл можно вычислить только численным способом. В случае скоростей из диапазона от ϑ до ϑ+Δϑ, где Δϑ<<ϑ, приближенно найдем
Численное вычисление дает
10.Число ударов молекул о стенку. Экспериментальная проверка распределения Максвелла. Границы применимости распределения Максвелла. Экспериментальная проверка Эксперимент Штерна Частота ударов о стенку Для нахождения частоты ударов молекул о стенку сосуда ν необходимо вычислить интеграл
где n – концентрация молекул, s – площадь стенки. При вычислении было учтено, что вклад вносят только молекулы, движущиеся в направлении стенки (находящейся на положительной части оси x) и имеющих направление скорости нормальное, по отношению к стенке.
11.Поперечное сечение.Средняя длина свободного пробега.Частотоа столкновений.Экспериментальное определение длины свободного пробега молекул. Поперечное сечение. При движении в газе молекула испытывает столкновения, в результате чего она изменяет направление своего движения. Вероятность столкновения с конкретным результатом описывается с помощью понятия поперечного сечения. Пусть падающая частица попадает на площадь S объема, в котором расположены
частицы-мишени с концентрацией n0. В слое толщины dx находится число частиц-мишеней n0Sdx, а сумма их поперечных сечений, которая как бы закрывает часть площади S, равна dS =
Частота столкновений. Падающая частица движется со средней скоростью <v>> и, следовательно, проходит длину среднего свободного пробега за время t= <l>/<v>. Поэтому средняя частота столкновений (среднее число столкновений за 1 с) равна
При рассмотрении столкновений одинаковых молекул в газах их чаще всего представляют в виде твердых шаров. Пусть молекулы-мишени неподвижны, а падающая на них молекула движется со скоростью <v>>. Очевидно, падающая молекула, пройдя расстояние х, столкнется со всеми молекулами-мишенями, центры которых находятся в круглом цилиндре с радиусом основания 2г0 и высотой х. Средняя длина свободного пробега равна высоте цилиндра, в котором в среднем находится одна молекула-мишень. Поэтому для определения среднего свободного пробега получаем уравнение
из которого следует, что Частота соударений между молекулами на основании равна
Процессы переноса Сталкиваясь друг с другом молекулы обмениваются импульсом и кинетической энергией. Благодаря этому газ, например, является проводником тепла. При этом, хотя в общем газ не находится в равновесном состоянии, можно говорить о локальном равновесии, т.е. о локальной температуре газа. Время восстановления локального равновесия характеризуется средним временем между столкновениями τст. Перенос трения (вязкость) Сила внутреннего трения (вязкость) описывается формулой Ньютона
где dF – элементарное приращение силы трения; η – коэффициент внутреннего трения (динамический коэффициент вязкости); u – скорость течения вещества как целого в направлении перпендикулярном к направлению действия силы (которая направлена в положительную сторону оси x); du / dx – градиент скорости течения вещества (знак минус указывает на то, что сила действует в направлении уменьшения градиента); s – элемент площади (нормальной к направлению действия силы), на которую оказывается воздействие. В случае идеального газа коэффициент внутреннего трения может быть найден в следующем виде
Поскольку lсрρ =const для заданного газа, то коэффициент трения идеального газа не зависит от его плотности (правило Максвелла).
Перенос массы (диффузия) Процесс переноса массы в положительном направлении оси x описывается уравнением Фика
где dm – элементарное приращение массы; D – коэффициент диффузии (самодиффузии); dρ / dx – градиент плотности (знак минус указывает на то, что диффузионный поток идет в направлении уменьшения градиента плотности); s – элемент площади (нормальной к направлению переноса), через которую идет поток; dt – элементарное приращение времени. В случае идеального газа коэффициент диффузии может быть найден в следующем виде
Данный коэффициент диффузии описывает перенос массы в идеальном газе из одинаковых молекул (самодиффузия), когда в каком то его области возникает отличный от нуля градиент плотности. В том случае, если смешиваются два газа из различных молекул, возникает явление называемое взаимной диффузией, когда каждый из газов проникает в другой. Взаимная диффузия Процесс взаимной диффузии двух газов описывается системой уравнений
где индексы «1» и «2» различают первый и второй газы; ϑ – гидродинамическая скорость потока газа как целого; D 12 = D 21 – коэффициент взаимной диффузии. При записи данных выражений предполагалось, что n 1+ n 2=const. Ультраразреженный газ Если длина свободного пробега молекул превышает линейные размеры сосуда, в котором заключен газ, то такой газ называют ультраразреженным. В таком газе молекулы не сталкиваются друг с другом, поэтому все явления переноса протекают иначе, чем в обычном идеальном газе. Молекулы сталкиваются только со стенками сосуда. Диффузия в твердом теле Диффузия (самодиффузия)в твердых кристаллических телах осуществляется главным образом следующими тремя путями. 1. Если в соседнем узле кристаллической решетки имеется вакансия, то один из соседних атомов может перескочить в вакантный узел. 2. Если атом покинул свой узел, а рядом нет вакансии, то он располагается между узлами. 3. Может произойти обмен атомами в соседних узлах решетки. Коэффициент диффузии при этом имеет вид Ультраразреженный газ Если длина свободного пробега молекул превышает линейные размеры сосуда, в котором заключен газ, то такой газ называют ультраразреженным. В таком газе молекулы не сталкиваются друг с другом, поэтому все явления переноса протекают иначе, чем в обычном идеальном газе. Молекулы сталкиваются только со стенками сосуда.
Барометрическая формула Для изменения давления с высотой, при постоянной температуре, можно получить следующее выражение, называемое барометрической формулой, применяется для исследования как классических, так и квантовых систем. 15.Барометрическая формула.Экспериментальное подтверждение распределения Больцмана. Атмосфера планет. Потенциальная энергия частицы массы т в поле тяготения шарообразного небесного тела равна
где М — масса тела, г — расстояние от центра тела до частицы, G — гравитационная постоянная. Атмосфера планет, в том числе и Земли, не находится в равновесном состоянии. Например, вследствие того что атмосфера Земли находится в неравновесном состоянии, ее температура не постоянна, как это должно было бы быть, а изменяется с высотой (уменьшается с увеличением высоты). Поскольку в конечном счете все системы стремятся к равновесному состоянию, то атмосфера планет постепенно рассеивается. У некоторых из небесных тел, например у Луны, атмосфера полностью исчезла, другие, например Марс, имеют очень разреженную атмосферу. Таким образом, атмосфера Луны уже достигла равновесного состояния, а атмосфера Марса уже находится близко к достижению равновесного состояния. У Венеры атмосфера очень плотная и, следовательно, находится в начале пути к равновесному состоянию. Для количественного рассмотрения вопроса о потере атмосферы планетами необходимо принять во внимание распределение молекул по скоростям. Силу земного притяжения могут преодолеть лишь молекулы, скорость которых превосходит вторую космическую. Эти молекулы находятся в «хвосте» распределения Максвелла и их относительное число незначительно. Тем не менее за значительные промежутки времени потеря молекул является чувствительной. Поскольку вторая космическая скорость
у тяжелых планет больше, чем у легких, интенсивность потери атмосферы у массивных небесных тел меньше, чем у легких, т. е. легкие планеты теряют атмосферу быстрее, чем тяжелые. Время потери атмосферы зависит также от радиуса планеты, температуры, состава атмосферы и т. д. Экспериментальная проверка распределения Больцмана. Опыт перрена При выводе распределения Больцмана не налагалось никаких ограничений на массу частиц. Поэтому в принципе оно применимо и для тяжелых частиц. Возьмем в качестве этих частиц, например, песчинки. Ясно, что они расположатся в некотором слое у дна сосуда. Строго говоря, это является следствием распределения Больцмана. При больших массах частиц показатель экспоненты столь быстро изменяется с высотой, что равен нулю везде за пределами слоя песка. Что касается пространства внутри слоя, то там надо принять во внимание объем песчинок. Для того чтобы тяжелые частицы не «осели на дно», а распределились в достаточно большом слое по высоте, необходимо, чтобы их потенциальная энергия была достаточно малой. Этого можно достигнуть, помещая частицы в жидкость, плотность которой лишь на немного меньше плотности материала частиц. Обозначив плотность и объем частиц р и t, а плотность жидкости — р0, видим, что сила, действующая на частицу, равна t (р — р0) g. Следовательно, потенциальная энергия такой частицы на высоте h от дна сосуда равна
Поэтому распределение концентрации этих частиц по высоте дается формулой
Чтобы эффект был достаточно хорошо заметен, частицы должны быть достаточно малыми. Число таких частиц на разных высотах в сосуде считают с помощью микроскопа Барометрическая форму л а. Поскольку формулой давление однозначно выражается через температуру, то распределение Больцмана
позволяет сразу, без дополнительных вычислений написать распределение давлений при тех же условиях, при которых справедлива эта формула, т. е. в условиях равновесия (T= const). Поэтому в случае изотермической атмосферы распределение давления с высотой h дается для каждой компоненты формулами.
Воздух в основном состоит из кислорода и азота. Поэтому формула для изменения давления в нем с высотой имеет вид
близки друг к другу и это изменение несущественно. Упомянуто же здесь лишь для теоретической полноты картины. Фактически смесь газов в отношении давления можно рассматривать как один газ со средней массой молекул
Учитывая, что [m/(kТ)] = ро(r o)/ро-> гДе Ро(ro) и Ро являются плотностью и давлением при h = 0, можно барометрическую формулу записать- в виде.
причем у поверхности Земли принимается р0 = 101,325 кПа. При этом считается, что температура с высотой не изменяется. Если выражать высоту в километрах, то барометрическую формулу удобно также представить в виде (принимая в формуле температуру равной 0°С)
Температура Температура является количественной мерой «нагретости» тела. Более нагретым является то, «нагретость» которого уменьшается при длительном контакте с другим телом, принимаемым в этом случае, по определению, за менее нагретое. Степень «нагретости» тела измеряется по характеристикам материальных тел, зависящих от «нагретости». Измерение «нагретости» сводится к измерению некоторой величины тела, которая изменяется с изменением «нагретости» тела. Тело, выбираемое для измерения «нагретости», называется термометрическим, а величина, посредством которой измеряется «нагретость», называется термометрической величиной. Наиболее широко известными являются «нагретость», при которой кипит вода при атмосферном давлении, и «нагретость», при которой она замерзает. Эти реперные точки называются точкой кипения воды и точкой замерзания. Температурой называется числовое значение величины, с помощью которой характеризуется «нагретость» тела. Температура выражается в градусах. Пусть точке кипения присваивается температура t2, а точке замерзания — температура t1, тогда градусом температуры называется величина
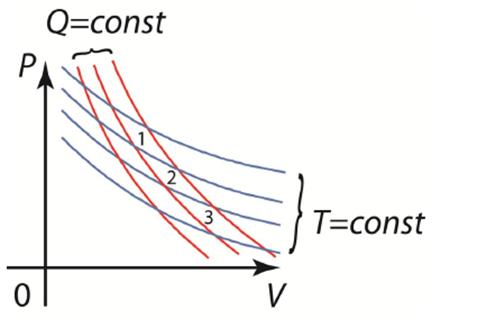
где l2 и l1 - термометрические величины термометрического тела в точках кипения и замерзания воды, соответственно. Термодинамическая шкала На основании 2-й теоремы Карно можно установить абсолютную термодинамическую шкалу температур, не зависящую от термометрического тела. Рассмотрим систему изотерм и адиабат. Фигуры 1, 2, 3, заключенные между двумя соседними изотермами и двумя адиабатами, являются циклами Карно.
Из выражения для КПД цикла Карно можно записать последовательность соотношений
Т.е. если задать какую-нибудь реперную точку (например, температуру тройной точки воды 273,16 К), то проведя последовательность прямых обратимых циклов Карно можно вычислить произвольную температуру (в произвольном процессе), если измерить соответствующее величины Q. Такое определение температуры не зависит от термометрического тела. Оно впервые было дано Кельвином. В честь которого была названа единица абсолютной термодинамической температуры. Отрицательные абсолютные температуры Понятно, что отрицательная абсолютная термодинамическая температура не имеет физического смысла. Тем не менее, в квантовых системах понятие отрицательной абсолютной температуры имеет вполне определенный смысл: это мера способа заполнения квантовых уровней энергии частицами. Если частицы заполняют сначала нижние энергетические уровни, так, что на более высоком уровне частиц меньше, то температура положительна и совпадает по значению с термодинамической. Если же создается инверсность населенностей, т.е. на более низко расположенном уровне частиц меньше, чем на более высоком, то температуре приписываются отрицательные значения. Тем не менее, такие значения все же не имеют физического смысла. Метастабильные состояния Эксперименты также показывают, что участки изотермы AB и DE могут быть реализованы. Данные участки соответствуют метастабильным состояниям. Эти состояния почти не устойчивы. Участок AB соответствует состоянию переохлажденного пара, а участок DE – состоянию перегретой жидкости. Состояние переохлажденного пара можно получить с помощью быстрого адиабатического охлаждения пара до температур меньших температуры парообразования, а состояние перегретой жидкости – с помощью медленного нагрева чистой жидкости до температур больших температуры кипения. Однако, малейшая соринка, попавшая в емкость с веществом в метастабильном состоянии, приводит к быстрой конденсации переохлажденного пара или бурному вскипанию перегретой жидкости.
Отличие результатов К сожалению, простая теория, связанная с использованием уравнения ВдВ не всегда адекватно описывает реальную ситуацию. Основные отличия следующие. 1. Для данного вещества постоянные а и b в уравнении Ван-дер-Ваальса должны быть независимыми от температуры. В действительности же они зависят от температуры. 2. Из соотношения критических параметров следует, что величина
должна быть универсальной постоянной для всех веществ. В действительности же она изменяется.Например, для воды она равна 0,23, а для гелия 0,31. 3. Соотношение V0,кр=3b не соблюдается. Более точным соотношением является V0,кр≈2b. 4. В области двухфазных состояний уравнение Ван-дер-Ваальса не обосновано теоретически и дает расхождения с экспериментом. Внутренняя энергия газа ВдВ Взаимодействие между молекулами газа ВдВ обусловливает их взаимную потенциальную энергию. Поэтому, наряду с величиной νCVdT, в элементарное изменение внутренней энергии газа dU должна входить работа против внутренних сил притяжения dA’= Pвнутр dV. Следовательно, для газа Ван-дер-Ваальса
Эффект Джоуля-Томсана Пропуская реальный газ по теплоизолированной трубке с пористой перегородкой, Джоуль и Томсон обнаружили, что при расширении, которым сопровождается прохождение газа через перегородку, температура его несколько изменяется. В зависимости от начальных давления и температуры изменениеприращения температуры ΔT имеет различные знаки («плюс» или «минус»). Это явление получило название эффекта Джоуля-Томсона. Если температура газа понижается (ΔT <0), эффект называется положительным; если газ нагревается (ΔT >0), эффект называется отрицательным. Пусть индексом «1» выделены, параметры, описывающие начальное состояния газа, а индексом «2» обозначим параметры, соответствующие его конечному состоянию (после расширения) Можно доказать, что в эксперименте Джоуля и Томсона сохраняется энтальпия, т.е. выполняется условие
Таким образом, знак эффекта Джоуля-Томсона определяется знаком выражения, стоящего в квадратных скобках. - эффект получается нулевым. Следует заметить, что эффект Джоуля-Томсона всецело обусловлен отклонениями газа от идеальности. Для идеального газа энтальпия H1 имеет вид
а условие равенства энтальпий принимает вид
Т.е. эффект является нулевым.
Насыщенный пар Если покинувшие жидкость молекулы удаляются из пространства вблизи поверхности жидкости, то в конце концов вся жидкость испарится. Если же молекулы, покинувшие жидкость, не удаляются, а удерживаются в замкнутом объеме около поверхности жидкости, то дальнейший процесс развивается по-другому. Покинувшие жидкость молекулы образуют пар. Молекулы пара, попавшие в область вблизи поверхности жидкости, силами притяжения втягиваются в жидкость. Таким образом, скорость испарения уменьшается. При дальнейшем увеличении плотности пара достигается такая ситуация, когда число молекул, покидающих жидкость за некоторое время, равно числу молекул, возвращающихся в жидкость за то же время. Наступает состояние динамического равновесия. Пар в состоянии динамического равновесия с жидкостью называется насыщенным. С увеличением плотности насыщенных паров поверхностное натяжение жидкости уменьшается, поскольку силы, направленные внутрь жидкости, уменьшаются ввиду роста противоположно направленных сил со стороны насыщенного пара. Отсюда же следует, что скрытая теплота парообразования с повышением температуры уменьшается. При критической температуре плотность насыщенных паров становится равной плотности жидкости и различие между ними исчезает. Это означает, что и поверхность исчезает, и, следовательно, поверхностное натяжение и скрытая теплота парообразования при критической температуре обращаются в нуль. При конденсации пара в жидкость его молекулы взаимно притягиваются, в результате чего их скорости, а следовательно, и их кинетическая энергия возрастают. Это ведет к нагреванию образующейся жидкости: теплота, затраченная при испарении, отдается обратно при конденсации пара. Вириальное ур состояния. Сжижение газов Эффект Джоуля-Томсона используется для сжижения газов, путем их охлаждения. Широко известен промышленный метод Линде.
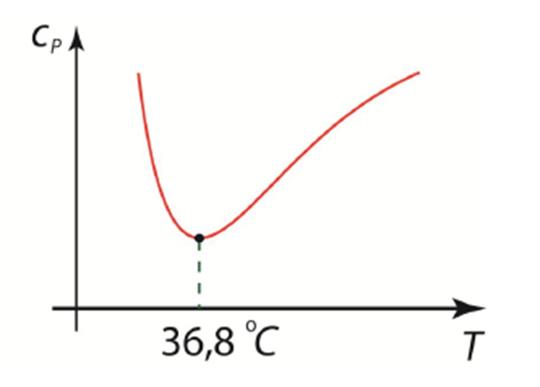
Жидкие кристаллы Жидкие кристаллы проявляют упорядоченность, которая является промежуточной между упорядоченностью жидкости и твердых тел, приводящей к соответствующей анизотропии их свойств. В соответствии с этим жидкие кристаллы делятся на две группы. Первая группа жидких кристаллов, называемых смектиками, характеризуется одномерной пространственной упорядоченностью. Жидкость представляется состоящей из параллельных жидких слоев, регулярно следующих друг за другом и отличающихся друг от друга упорядоченностью структуры. Вторая группа жидких кристаллов, называемых нематиками, не имеет пространственной упорядоченности, а характеризуется ориентационной упорядоченностью их молекул. Их молекулы сильно вытянуты, и ориентационная упорядоченность возникает из-за преимущественной ориентации этих длинных молекул. У смектиков молекулы также сильно вытянуты. Поэтому можно сказать, что особенностью жидких кристаллов с молекулярной точки зрения является вытянутая структура их молекул, приводящая к анизотропии свойств. Теплоемкость жидкостей Внутренняя энергия жидкостей определяется не только кинетической энергией тепловых движений молекул, но и их потенциальной энергией взаимодействия. Опыт показывает, что теплоемкость жидкостей зависит от температуры, причем вид зависимости у разных жидкостей различный. У большинства из них теплоемкость с повышением температуры увеличивается, но есть и такие, у которых, наоборот, - уменьшается. У воды удельная теплоемкость с повышением температуры сначала падает, а затем, пройдя через минимум, начинает расти.
Основное уравнение кинетической теории газов. Основные газовые законы. Понятие температуры. Идеально-газовая шкала температур. . Законы идеальных газов: Закон Бойля-Мариотта: если Т, m=const, то Молем вещества называют такое его количество, в котором находится NA = 6,02∙1023 молекул; NA - число Авогадро. Нормальные условия соответствуют температуре 273,15 градусов Кельвина (273,15 К) и давлению (1,013)·105Па Молярная масса = массе 1-го моля вещества. Обозначается M (не путать с m – массой газа). Количество молей ν = m/M = N/NA; N – число молекул в веществе. Уравнение состояния идеального газа Законы идеального газа можно свести к одному уравнению (уравнению Менделеева-Клапейрона), Температур а в молекулярной физике – мера хаотического движения молекул: чем больше температура, тем быстрее движутся молекулы. В термодинамике работают с абсолютной или термодинамической температурой, измеряемой по шкале Кельвина (K ): T = 273,15 + t, где t – температура в градусах Цельсия. Например, 10 градусов Цельсия соответствует температура 283,15 К, а нулю градусов Цельсия – температура 273,15 К. Идеально-газовая шкала: Было замечено, что при постоянном объеме и массе идеального (т.е. реального разреженного) газа его давление зависит от температуры по закону Основное уравнение МКТ связывает давление с кинетической энергией молекул: Основное уравнение МКТ можно получить в следующем виде:
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 682; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.162.204 (0.126 с.) |
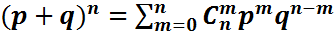 Если p+q=1 и p, q>0, то бином Ньютона превращается в биноминальное распределение
Если p+q=1 и p, q>0, то бином Ньютона превращается в биноминальное распределение 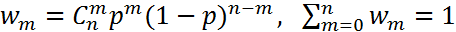 Биноминальное распределение соответствует распределению вероятности того, что при n испытаниях рассматриваемое событие (имеющее вероятность p) реализуется m раз. В случае больших n и m воспользуемся формулой Стирлинга, получим
Биноминальное распределение соответствует распределению вероятности того, что при n испытаниях рассматриваемое событие (имеющее вероятность p) реализуется m раз. В случае больших n и m воспользуемся формулой Стирлинга, получим  Дифференцируя это выражение по m и приравнивая к нулю, получим
Дифференцируя это выражение по m и приравнивая к нулю, получим 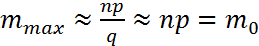 где m0 – соответствует максимуму биноминального распределения.
где m0 – соответствует максимуму биноминального распределения. В пределе получим
В пределе получим  - распределение Пуассона.
- распределение Пуассона.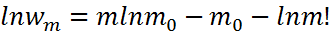 или пользуясь формулой Стирлинга
или пользуясь формулой Стирлинга  Разложим последнее выражение в ряд Тейлора
Разложим последнее выражение в ряд Тейлора ,
,  - называется распределением Гаусса.
- называется распределением Гаусса.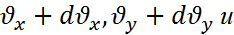
 равно
равно  Для нахождения нормировочного
Для нахождения нормировочного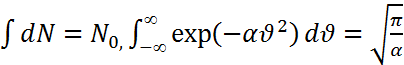 . Распределение Максвелла покомпонентам скорости имеет вид
. Распределение Максвелла покомпонентам скорости имеет вид 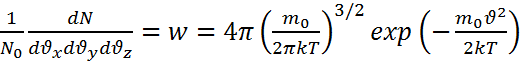 , и распределение Максвелла по
, и распределение Максвелла по




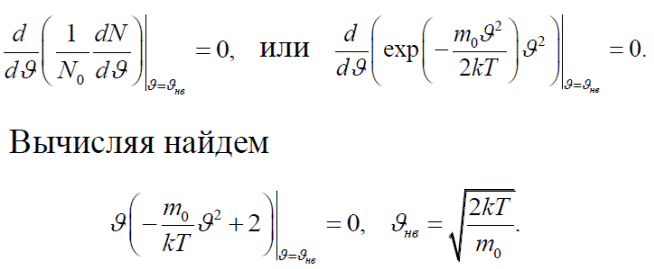
 Тогда распределение Максвелла примет т.н. приведенный вид
Тогда распределение Максвелла примет т.н. приведенный вид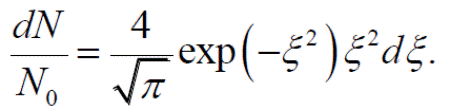


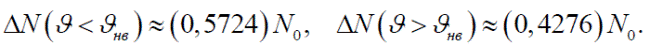
 Эксперимент Элдриджа
Эксперимент Элдриджа
 n0S dx. Отсюда следует, что вероятность того, что падающая частица попадет в одну из частиц-мишеней в слое dx, равна1
n0S dx. Отсюда следует, что вероятность того, что падающая частица попадет в одну из частиц-мишеней в слое dx, равна1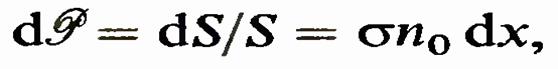 где использовано определение вероятности. Это есть определение поперечного сечения а рассматриваемого процесса. Средняя длина свободного пробега. Величины
где использовано определение вероятности. Это есть определение поперечного сечения а рассматриваемого процесса. Средняя длина свободного пробега. Величины  , из которого следует, что
, из которого следует, что 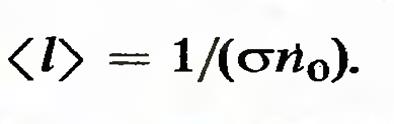


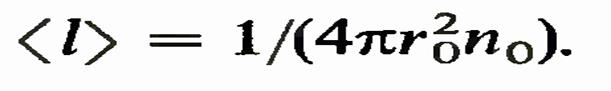

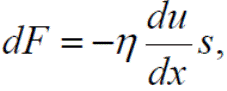
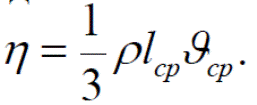



 где D 0 – постоянна я определяемая свойствами вещества; W – энергия активации диффузии.
где D 0 – постоянна я определяемая свойствами вещества; W – энергия активации диффузии.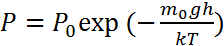 , где m0 – масса молекулы; h – высота. С учетом того, что
, где m0 – масса молекулы; h – высота. С учетом того, что  получим
получим  , Барометрическая формула является частным случаем общего распределения, называемого распределением Больцмана. В самом деле, учитывая, что потенциальная энергия молекулы на высоте h
, Барометрическая формула является частным случаем общего распределения, называемого распределением Больцмана. В самом деле, учитывая, что потенциальная энергия молекулы на высоте h 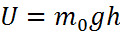 и
и  , получим
, получим  , - распределение Больцмана. Данное распределение справедливо не только для гравитационного поля, но и для любого другого однородного (и не только) поля сил. Если на идеальный газ действует потенциальное поле (например, сила тяжести), то распределение Максвелла должно быть изменено с учетом распределения Больцмана. Подставляя распределение Больцмана в распределение Максвелла, получим
, - распределение Больцмана. Данное распределение справедливо не только для гравитационного поля, но и для любого другого однородного (и не только) поля сил. Если на идеальный газ действует потенциальное поле (например, сила тяжести), то распределение Максвелла должно быть изменено с учетом распределения Больцмана. Подставляя распределение Больцмана в распределение Максвелла, получим  - распределение Максвелла-Больцмана. Распределение Максвелла-Больцмана является частным случаем общего распределения, называемого распределением Гиббса (полученного в 1901 г.):
- распределение Максвелла-Больцмана. Распределение Максвелла-Больцмана является частным случаем общего распределения, называемого распределением Гиббса (полученного в 1901 г.): 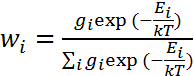 где gi – статистический вес (кратность вырождения (повторения)) рассматриваемого состояния i системы, имеющей энергию Ei. Распределение Гиббса широко
где gi – статистический вес (кратность вырождения (повторения)) рассматриваемого состояния i системы, имеющей энергию Ei. Распределение Гиббса широко
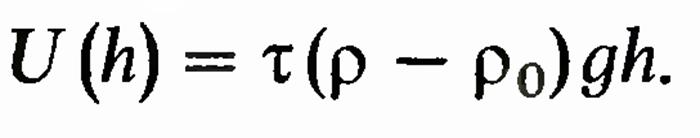


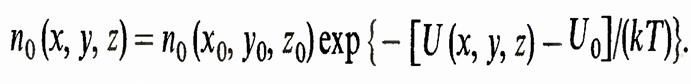
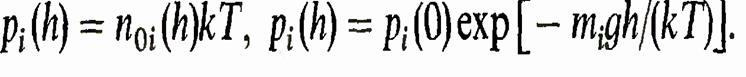
 Однако массы молекул азота и кислорода
Однако массы молекул азота и кислорода


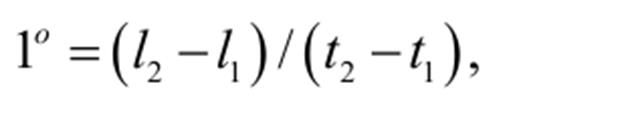
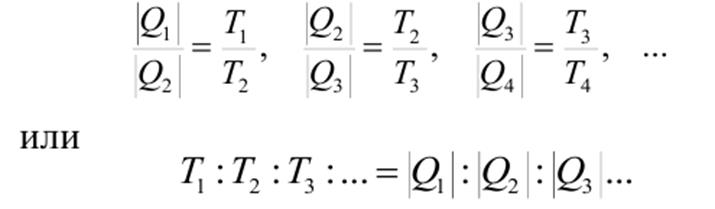

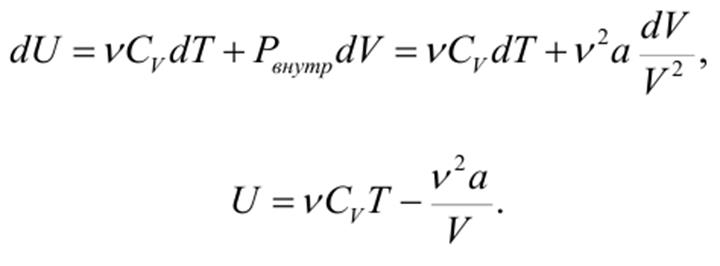



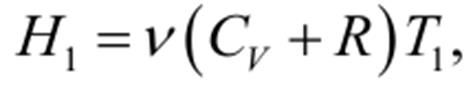


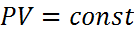 Закон Гей-Люссака: если P, m = const, то
Закон Гей-Люссака: если P, m = const, то  Закон Шарля: если V, m = const, то
Закон Шарля: если V, m = const, то 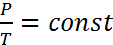 Законы идеальных газов: Закон Дальтона: давление смеси газов равно сумме парциальных давлений каждого из газов, составляющих смесь. Закон Авогадро: один моль газа при нормальных условиях занимает объем равный 22,41 л.
Законы идеальных газов: Закон Дальтона: давление смеси газов равно сумме парциальных давлений каждого из газов, составляющих смесь. Закон Авогадро: один моль газа при нормальных условиях занимает объем равный 22,41 л.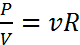 где R=8,31 Дж/(моль·К) – универсальная газовая постоянная. Уравнение Менделеева-Клапейрона -допускает несколько различных форм записи:
где R=8,31 Дж/(моль·К) – универсальная газовая постоянная. Уравнение Менделеева-Клапейрона -допускает несколько различных форм записи: 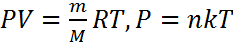 где n – концентрация молекул; k = R/NA = 1,38·10-23Дж/К – постоянная Больцмана.
где n – концентрация молекул; k = R/NA = 1,38·10-23Дж/К – постоянная Больцмана. где P0-давление при начальной температуре. С помощью закона Шарля получим
где P0-давление при начальной температуре. С помощью закона Шарля получим 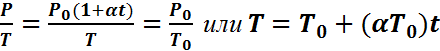 . Экспериментально измеренное α = 1/273,15 К-1
. Экспериментально измеренное α = 1/273,15 К-1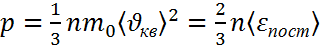 ,где
,где 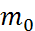 –масса одной молекулы,
–масса одной молекулы,  -средняя квадратичная скорость движения молекул,
-средняя квадратичная скорость движения молекул,  -средняя кинетическая энергия поступательного движения одной молекулы.
-средняя кинетическая энергия поступательного движения одной молекулы. , где N-число молекул в объёме сосуда V; m0-масса одной молекулы; P-давление газа на стенки сосуда;
, где N-число молекул в объёме сосуда V; m0-масса одной молекулы; P-давление газа на стенки сосуда; 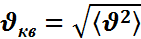 - средняя квадратичная скорость движения молекул в газе. Основное уравнение МКТ можно преобразовать, если учесть, что
- средняя квадратичная скорость движения молекул в газе. Основное уравнение МКТ можно преобразовать, если учесть, что  имеем
имеем 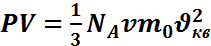 , или
, или  Пользуясь уравнением Менделеева-Клапейрона найдем
Пользуясь уравнением Менделеева-Клапейрона найдем  , где k-постоянная Больцмана. С учетом того, что
, где k-постоянная Больцмана. С учетом того, что 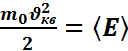 - средняя кинетическая энергия движения молекулы, получим
- средняя кинетическая энергия движения молекулы, получим 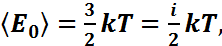 где i – число степеней свободы молекулы газа (для поступательного движения молекулы i=3). Из этого выражения следует, что на одну степень свободы приходится (1/2)kT энергии (теорема Больцмана). Таким образом, температура – мера средней кинетической энергии движения молекул газа.
где i – число степеней свободы молекулы газа (для поступательного движения молекулы i=3). Из этого выражения следует, что на одну степень свободы приходится (1/2)kT энергии (теорема Больцмана). Таким образом, температура – мера средней кинетической энергии движения молекул газа.


