
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Достоинства вертикальной оси
1.Возможность применения конструкции меньших размеров 2.Отсутствие механизмов ориентации по ветру 3.Рабочие элементы располагаются близко к земле, что облегчает их обслуживание 4.Невысокая минимальная рабочая скорость ветра (система начинает производить электричество при скорости ветра в 2-2,5 метра в секунду) 5.Позволяет строительство в местах, где невозможно возведение высоких сооружений 6.Во время работы производит меньше шума Недостатки вертикальной оси 1.Из-за потерь на вращении против потока воздуха большинство ветрогенераторов с вертикальной осью вращения почти в два раза менее эффективны, чем с горизонтальной 2.Поскольку некоторые элементы системы находятся внизу и, соответственно, под весом конструкции, то их ремонт или замена могут быть невозможны без демонтажа самой мельницы. Конечно, если такое не предусмотрено конструкцией конкретного генератора Теория идеального ветряка Теория Жуковского.Теория идеального ветряка, как ее сейчас называют, не создавалась Н.Е. Жуковским специально, а представляет собой вводный параграф к последней из трех статей, посвященных ветрякам, написанных в 1920 году. Внимание к теме ветряков у Жуковского было вызвано предложениями одного изобретателя сулившего огромную мощность от своей ветроустановки. Жуковский имел обыкновение в течение ряда лет вновь и вновь возвращаться к ранее поднятым темам и с присущим ему блеском выяснять суть проблемы до конца. Но последовавшие болезни, смерть любимицы умницы дочери не оставили возможности 73 летнему ученому продолжить работы по данной теме. Суть теории в следующем.
Когда поток воздуха набегает на вращающийся ветряк, то скорость потока уменьшается. В плоскости ветряка она равна Vв — v1, а далеко за ветряком Vв — v2. Работа, производимая ветром, равна разности кинетических энергий набегающего и отходящего воздуха.
С другой стороны уменьшение импульса воздушного потока Δp = m1v2 = FΔt вызывает силу, воздействующую на лопасти ветряка. Замедленное прохождение воздуха через плоскость ветряка, преодолевающего сопротивление лопастей, вызвано работой, совершаемой ветром.
Приравнивая 3.1.1 и 3.1.2 и решая, находим
То есть замедление скорости ветра за ветроколесом в два раза больше замедления скорости в плоскости колеса.
КИЭВ в данном случае составит величину
Максимальный КИЭВ достигается при v1 = 1/3 Vв и составляет hmax = 16/27 = 0,593 Данная теория, несмотря на ее сугубую абстрактность, является базовой в теории пропеллерных ветроустановок. Поэтому рассмотрим ее более внимательно. Во-первых, обратим внимание на формулу КИЭВ 3.1.5. Скорость потока в плоскости ветроколеса на треть меньше, чем скорость ветра, следовательно, треть набегающего потока не может пройти сквозь ветроколесо и огибает его снаружи. Поэтому в числителе подставлена масса m1, т.е. масса воздуха прошедшая через ветроколесо, она на треть меньше полной массы m набегающего воздуха, стоящей в знаменателе. Напомню, что воздух в ветроустановках испытывает столь ничтожные давления, что его можно считать несжимаемым. Повышенное давление перед ветроколесом не может служить резервуаром дополнительных масс сжатого воздуха. Воздух, отходящий в дальней зоне за ветроколесом, имеет скорость в одну треть от скорости ветра, следовательно, он уносит девятую часть энергии потока прошедшего сквозь ветроколесо. Произведение двух третей воздуха, прошедшего сквозь колесо на к.п.д. преобразования энергии, равный восьми девятым и составляет найденный КИЭВ 16/27. Входящий в формулу 3.1.2 импульс mv2 позволяет нам сделать важный вывод. Потеря скорости воздухом v2, а, следовательно, и отдаваемая ветроколесу энергия складывается из двух составляющих. Потери скорости до ветроколеса v1 и потери скорости после ветроколеса v2- v1. До ветроколеса поток теряет треть своей скорости и 5/9 своей энергии, которую передает колесу. После колеса поток теряет еще треть скорости и 3/9 первоначальной энергии. Оставшаяся 1/9 часть энергии уносится отходящим потоком. Понятно, что набегающий поток воздуха создает некое избыточное давление на передней плоскости лопастей, заставляющее вращаться ветроколесо. Поток, находящийся за ветроколесом, может отдать часть своей энергии ветроколесу, оставшемуся позади, только в том случае, если этот поток воздуха, расширяясь, создает разряжение за ветроколесом. Отрицательное давление на задней стороне лопаток увеличивает силу, вращающую ветроколесо. Можно составить уравнения Бернулли и получить те же результаты, что и у Жуковского, оперируя в выкладках понятием давления…
|
||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 641; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.159.10 (0.005 с.) |

 (3.1.1)
(3.1.1)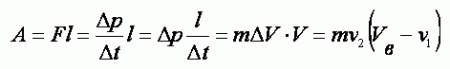 (3.1.2)
(3.1.2) (3.1.3)
(3.1.3) (3.1.4)
(3.1.4) > (3.1.5)
> (3.1.5)


