
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Заміна змінних в потрійному інтегралі ⇐ ПредыдущаяСтр 4 из 4
Нехай система функцій
здійснює взаємно-однозначне відображення області V в системі координат (х, у, z) в область V 1 в системі координат
де
У випадку переходу до циліндричних координат У випадку переходу до сферичних координат Приклад 10. Обчислити об’єм області, обмеженої еліпсоїдом Розв’язання. Знаходження об’єму v заданої області V за формулою
вимагає обчислити потрійний інтеграл. Цей інтеграл обчислено при розв’язанні прикладу 8. Покажемо, що відповідна заміна змінних дозволяє ці обчислення значно спростити. Зробимо заміну змінних: В цієї узагальненої сферичної системі координат
Якобіан переходу буде
1. Обчислити інтеграли: а) (Відповідь: а) 2. Оцінити інтеграл х (Відповідь: 24 < I < 72). 3. Обчислити де область D описується нерівностями: (Відповідь: 4. Обчислити інтеграл де V – область, яка обмежена площинами z = 0 та z = h і поверхнею обертання кривої у = z 2 навколо осі Oz. (Відповідь: 5. Обчислити інтеграл 2 х + 2 у + z – 6 = 0. (Відповідь: 6. Обчислити інтеграл (Відповідь: 7. Знайти об’єм тіла, яке обмежене поверхнями 4 z = х 2 + у 2 та х 2 + у 2 + z 2 = 12 (Відповідь: 8. Знайти об’єм тіла, обмеженого поверхнями х 2 + у 2 + z 2 = 16 та х 2 + у 2 + z 2 – 8 z = 0. Рекомендація: Спочатку використати формулу (Відповідь: 9. Обчислити об’єм області, яка обмежена поверхнями: а) сферою радіуса а; б) конусом з вершиною в центрі сфери і твірними, що нахилені до осі Оz під кутом Рекомендація: Розв’язування провести в сферичних координатах. Рівнянням сфери буде рівність r = а. Аналітичний опис області буде:
(Відповідь: 10. Знайти масу частини кулі радіуса R, яка розташована в першому октанті і має в кожній точці густину рівну відстані цієї точки від площини хОу. Рекомендація: густина розподілу маси (Відповідь: 11. Знайти масу тіла, обмеженого поверхнями: х 2 + у 2 + z 2 = 4 та 3 z = х 2 + у 2. Густина розподілу маси в кожній точці тіла: (Відповідь: 12. Обчислити об’єм частини кулі х 2 + у 2 + z 2 Рекомендація: Перейти до циліндричних координат. (Відповідь: 13. Обчислити об’єм області, яка обмежена поверхнями х 2 + у 2 = R 2 та z = х 2 + у 2. (Відповідь: 14. Переходом до сферичних координат обчислити інтеграл
(Відповідь: 15. Переходом до циліндричних координат обчислити
Невластиві інтеграли по області Основні поняття
Інтеграли по області Випадок нескінченної області. Якщо функція
де Dn – обмежена область така, що Якщо границя правої частини рівності (1) існує і не залежить від вибору області Dn, то відповідний невластивий інтеграл по області D називається збіжним. Якщо ця границя не існує або дорівнює нескінченності, то невластивий інтеграл називають розбіжним. Якщо підінтегральна функція Випадок розривної (необмеженої) функції. Якщо функція
де
Якщо границя правої частини (2) існує і не залежить від виду видалених областей діаметром Якщо Якщо в області інтегрування підінтегральна функція має розриви другого роду (стає необмеженою) на деякій лінії L або поверхні S, то ця особливість видаляється із області інтегрування, а потім видалена частина стягується до особливості. Приклад 11. Дослідити збіжність інтеграла Розв’язання. Заданий інтеграл є невластивим подвійним інтегралом по необмеженій області D, підінтегральна функція невід’ємна. Позначимо через DR – круг радіуса R з центром в початку координат. Тоді рівність (1) прийме вигляд:
Обчислимо подвійний інтеграл по області DR переходом до полярної системи координат:
Отже, Відповідь: невластивий інтеграл – збіжний і дорівнює Приклад 12. Дослідити збіжність інтеграла
Розв’язання. Задано невластивий подвійний інтеграл по обмеженій області від функції, яка необмежена на колі х 2 + у 2 = 4 і невід’ємна. Позначимо через
Обчислимо подвійний інтервал по області
Заданий інтеграл дорівнює
тому він збіжний. Зауваження: 1. Якщо підінтегральна функція Для обчислення абсолютно збіжного інтеграла по області межі інтегралів можна визначати у будь-якій системі координат. Якщо інтеграл по області абсолютно не збігається, то заміна змінних і переставлення порядку інтегрування потребують спеціального дослідження. 2. При дослідженні збіжності невластивих інтегралів по області часто застосовують порівняльні ознаки. Наприклад, якщо D є площиною, то для збіжності інтеграла Аналогічно в тривимірному просторі інтеграл від При досліджені невластивих інтегралів по області від функції, яка необмежена в ізольованій точці М 0 області D часто використовують порівняння з інтегралами Перший із вказаних інтегралів збігається при р < 2, а другий – при р < 3. Якщо особливості підінтегральної функції не ізольовані, то умову збіжності часто вдається одержати шляхом вибору такої системи координат, в якій координатні лінії проходять вздовж особливості.
1.Обчислити інтеграли: а) в)
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 520; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.107.191 (0.039 с.) |
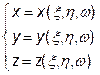
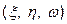 . Тоді перехід від змінних х, у, z до змінних
. Тоді перехід від змінних х, у, z до змінних 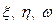 в потрійному інтегралі здійснюється за формулою:
в потрійному інтегралі здійснюється за формулою: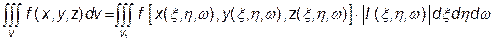 , (9)
, (9) – якобіан перетворення елемента об’єму області, причому
– якобіан перетворення елемента об’єму області, причому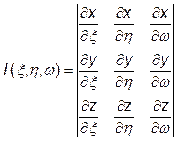 (10)
(10)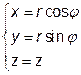 якобіан
якобіан 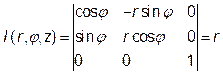
 якобіан
якобіан 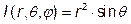 .
.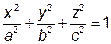 .
.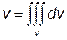
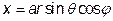 ,
, 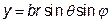 ,
, 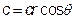 .
. рівняння еліпсоїда приймає вигляд: r = 1. Тому область інтегрування V 1 визначається системою нерівностей:
рівняння еліпсоїда приймає вигляд: r = 1. Тому область інтегрування V 1 визначається системою нерівностей: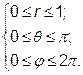
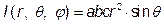 . Отже, за формулою (9) одержимо:
. Отже, за формулою (9) одержимо: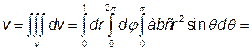 .
.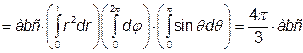

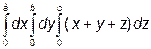 ; б)
; б) 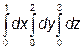 ; в)
; в) 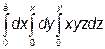 .
.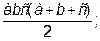 б) 6; в)
б) 6; в) 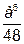
 , де D – куб:
, де D – куб: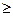 1; у
1; у 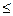 3; у
3; у 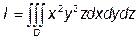 ,
,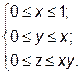
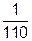 ).
). ,
,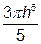 ).
). , де V – область, яка обмежена координатними площинами та площиною
, де V – область, яка обмежена координатними площинами та площиною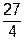 ).
). , де V – область, яка обмежена поверхнями: х = у 2; у = х 2; z = xy та z = 0.
, де V – область, яка обмежена поверхнями: х = у 2; у = х 2; z = xy та z = 0.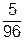 ).
).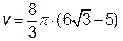 куб. од.).
куб. од.).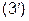 . При обчисленні подвійного інтеграла перейти до полярних координат.
. При обчисленні подвійного інтеграла перейти до полярних координат.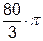 куб. од.).
куб. од.). ; в) двома площинами, які проходять через вісь Оz і утворюють з площиною хОz кути
; в) двома площинами, які проходять через вісь Оz і утворюють з площиною хОz кути 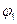 та
та 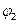
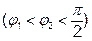 ; г) площиною хОу.
; г) площиною хОу.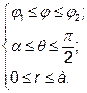
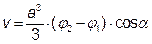 куб. од.).
куб. од.).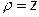 . Потрійний інтеграл обчислити переходом до сферичних координат.
. Потрійний інтеграл обчислити переходом до сферичних координат.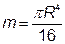 ).
).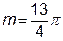 )
)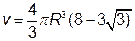 куб. од.).
куб. од.).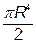 куб. од.).
куб. од.).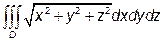 де D – куля радіуса R.
де D – куля радіуса R. ).
).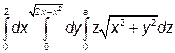 (Відповідь:
(Відповідь: 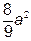 ).
). називають невластивими, якщо область інтегрування D необмежена або підінтегральна функція
називають невластивими, якщо область інтегрування D необмежена або підінтегральна функція 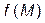 необмежена в деяких точках М області інтегрування. Невластиві інтеграли по області можуть бути збіжними або розбіжними.
необмежена в деяких точках М області інтегрування. Невластиві інтеграли по області можуть бути збіжними або розбіжними. , (1)
, (1) і
і  , тобто Dn розширюється за довільним законом і містить довільну точку область D.
, тобто Dn розширюється за довільним законом і містить довільну точку область D.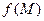 неперервна в замкненій обмеженої області D за виключенням точки М 0, то розглядають
неперервна в замкненій обмеженої області D за виключенням точки М 0, то розглядають , (2)
, (2)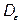 – область, яка одержується із області D шляхом видалення області діаметром e, яка містить точку М 0.
– область, яка одержується із області D шляхом видалення області діаметром e, яка містить точку М 0. , то відповідний невластивий інтеграл називається збіжним, в протилежному випадку – розбіжним.
, то відповідний невластивий інтеграл називається збіжним, в протилежному випадку – розбіжним. , то границя в (2) не залежить від виду видаленої області. В цьому випадку найчастіше видаляють окіл радіуса e точки М0.
, то границя в (2) не залежить від виду видаленої області. В цьому випадку найчастіше видаляють окіл радіуса e точки М0. , де область D – площина хОу.
, де область D – площина хОу. .
. .
. .
. .
. .
. .
.

 ,
, і
і 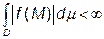 , то невластивий інтеграл по області
, то невластивий інтеграл по області  , тому потрібно використовувати інтеграл
, тому потрібно використовувати інтеграл  , який збігається р > 2 і розбігається при р < 2.
, який збігається р > 2 і розбігається при р < 2. на нескінченності збігається лише при р > 3.
на нескінченності збігається лише при р > 3.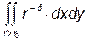 на площині та
на площині та  в просторі.
в просторі.
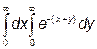 ; б)
; б) 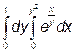 ;
;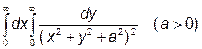 .
.


