
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Бюджетные модели цифровых частотомеров
Одним из последних моделей российской фирмы АКТАКОМ стали три частотомера: АСН-2801, АСН-3001 и АСН-3002 (рис.9.7). Частотомеры АСН-2801, АСН-3001 и АСН-3002 позволяют проводить измерения частоты в диапазоне от 10 Гц до 3 ГГц с максимальным разрешением 0,1 Гц и погрешностью порядка 10-5 %. При этом максимальная чувствительность на частоте 100 МГц составляет всего 0,8 мВ, что является очень неплохим показателем для частотомеров данного ценового сегмента. Рабочие температуры эксплуатации находятся в пределах от 0 °С до +50 °С при относительной влажности не более 90 % и давлении от 495 до 795 мм рт. ст.
Рисунок 9.7 – Универсальные цифровые частотомеры АСН – 2801, 3001,3002 Питание приборов осуществляется от аккумуляторных батарей, которых хватает на 6 часов непрерывной работы, или через сетевой адаптер. Помимо этого следует отметить возможность беспроводного измерения частоты радиопередающего устройства - например, сотового телефона - с помощью телескопической антенны. Это значительно упрощает процесс измерения частоты при проведении разного рода инженерных работ в полевых условиях. В этих условиях измерение параметров сигнала возможно на следующих расстояниях до передатчика: а) беспроводной телефон — до 0,3 метров; б) сотовый телефон — от 3 до 20 метров; в) СВ-источник — от 2 до 8 метров; г) КВ/УКВ-источник — от 3 до 30 метров. Цифровые частотомеры часто встраиваются в многофункциональные приборы, такие как мультиметры, функциональные генераторы, комбинированные приборы и т.д. Небольшое количество ручных частотомеров связано с тем, что функции измерения частоты сейчас есть у большинства мультиметров. Высокоточные измерения частоты (с погрешностью 0,005%) обеспечивают мультиметры американской фирмы FLUKE, например, FLUKE-187/189 до 999,99 МГц.
Тема 10. Мостовые методы измерения параметров элементов
В измерительной технике используют разнообразные измерительные мосты. Для измерения омического сопротивления получили распространение мосты постоянного и переменного тока. Различают схемы одинарных и двойных мостов постоянного тока. Мосты постоянного тока
Одинарный мост постоянного тока (рис.10.1) состоит из четырех резисторов R1-R4, образующих четыре плеча схемы, источника питания Е и вольтметра с нагрузкой Rн.
Рисунок 10.1 – Схема одинарного моста постоянного тока Напряжение на нагрузке (вольтметре) равно
Условием баланса (уравновешивания) такого моста является отсутствие напряжения на нагрузке, что обеспечивается равенством произведений величин сопротивлений противоположных плеч моста:
Равновесие моста достигается изменением сопротивления потенциометра R4 и отношения R2/R3. Отношение сопротивлений R2/R3 называют масштабным множителем, его значение выбирается равным 10n, где n - целое положительное или отрицательное число с переходом через нуль. Плечо R4 моста в этом случае называют плечом уравновешивания. Важным параметром мостовой схемы является чувствительность, т.е. минимальное изменение измеряемого сопротивления Rх (датчик температуры, давления и т.д.), которое вызывает нарушение баланса схемы, регистрируемого вольтметром. Чувствительность схемы зависит не только от чувствительности вольтметра, но и от сопротивлений резисторов, входящих в состав его плеч. Сопротивление плеч моста рекомендуется выбирать попарно равноплечими или использовать полностью равноплечий мост, т.е. мост, для которого R1 = R2 = R3 = R4. Одинарные четырехплечие мосты применяют для измерения сравнительно больших сопротивлений, от десятков Ом и выше. При измерении малых сопротивлений возникают погрешности, обусловленные влиянием сопротивлений соединительных проводов. Уменьшение влияния сопротивления контактов и соединительных проводов можно обеспечить схемным решением. Так, при измерении сопротивлений, меньших 10 Ом, используют четырехзажимное включение Rx. Для измерения малых сопротивлений используют также двойные измерительные мосты (мост Томсона), где схемным путем практически исключается влияние соединительных проводов на результат измерения.
Мосты переменного тока
Метод измерительного моста переменного тока находит широкое применение для измерения омического сопротивления, емкости, тангенса угла потерь, индуктивности, добротности. В отличие от мостов постоянного тока здесь одну диагональ моста включен источник переменного напряжения (генератор низкой частоты), в другую - нулевой индикатор переменного напряжения, плечи моста - двухполюсники с полным сопротивлением Z (рис.10.2).
Рисунок 10.2 – Схема моста переменного тока Равновесие моста достигается при условии равенства произведений комплексных сопротивлений противоположных плеч: Z1Z4 = Z2Z3. (10.3) В показательной форме равенство будет иметь вид
где Равенство (10.4) представим в виде двух равенств: -равенство произведений модулей комплексных сопротивлений противолежащих плеч:
- равенство сумм аргументов комплексных сопротивлений противоположных плеч:
Равенства (10.5) и (10.6) определяют условия равновесия моста. Они показывают, что мост переменного тока нужно уравновешивать регулировкой активной и реактивной составляющих плеч, т.е. равновесие осуществляется по модулям и фазам. При этом уравнения (10.5) и (10.6) равносильны и оба обязательны для достижения равновесия моста. Условие (10.6) указывает, при каком расположении плеч в зависимости от их характера можно уравновесить схему. Если смежные плечи, например третье и четвертое (рис.10.2), имеют чисто активные сопротивления R3 и R4, т.е. φ3 = φ4 = 0, то два других смежных плеча могут иметь или индуктивный, или емкостный характер. Если противоположные плечи чисто активные, то одно из двух других сопротивлений должно быть индуктивным, а другое – емкостным. При алгебраической форме представления комплексного сопротивления Z = R + jX, где R – вещественная часть, представляющая активную составляющую; X – мнимая часть, представляющая реактивную составляющую. В алгебраической форме равенство (10.3) примет вид (R1 + jX1)(R4 + jX4) = (R2 + jX2)(R3 + jX3) (10.7) Это равенство обеспечивается при одновременном выполнении равенства активных и реактивных частей, т.е. real: R1R4 – X4X1 = R2R3 – X2X3 и Im: R1X4 + R4X1 = R2X3 + R3X2. Рассмотрим мост для измерения емкости и угла потерь конденсаторов (рис.10.3).
Рисунок 10.3 – Схема моста для измерения емкости Два его плеча составлены из магазинов сопротивлений R2 и R4. Третье плечо образовано последовательно соединенными образцовыми конденсатором Со и переменным резистором с малым сопротивлением Ro. В четвертое плечо включен измеряемый конденсатор Сх, сопротивление потерь в котором Rx. Полные сопротивления плеч моста равны:
Подставив в формулу равновесия моста (10.3) эти значения, получим
Приравняв отдельно вещественные и мнимые части, получим
Из анализа векторной диаграммы цепи RxCx следует, что угол δх, дополняющий до 90о φх, определяется как tg δх = ωRxCx. Уравновешивание моста переменного тока для измерения индуктивности рассмотрим на примере схемы, представленной на (рис.10.4).
Рисунок 10.4 – Схема моста для измерения индуктивности Здесь для измерения индуктивности Lx используют образцовый конденсатор Со, включенный в плечо, противоположное плечу с измеряемой индуктивностью. Параллельно с конденсатором Со включен резистор Ro. В остальные плечи включены магазины сопротивлений R2 и R3. Полные сопротивления плеч равны
Равновесие моста согласно (10.2) определяется как
Отсюда следует, что
На основании изложенного можно заключить, что для мостов, у которых два плеча содержат только активные сопротивления, а два других – реактивные (рис.10.3 и 10.4), справедливы следующие утверждения: - если активные сопротивления находятся в смежных плечах (рис.10.3) R2 и R4 и φ2 = φ4 = 0, то два других плеча должны содержать сопротивления одного характера (индуктивного или емкостного), что обеспечивает выполнение условия φ1 = φ3; - если активные сопротивления расположены в противоположных плечах (рис.10.4) R2 и R3 и φ2 = φ3 = 0, то характер сопротивлений двух других плеч должен быть противоположным, что обеспечивает выполнение условия φ1 = -φ4. Погрешности измерений параметров цепей с использованием рассмотренных мостов составляет сотые доли % от измеряемой величины. Они обусловлены следующими причинами: - погрешностью значений образцовых элементов моста; - влиянием паразитных связей между элементами схемы; - влиянием нестабильностью параметров элементов схемы; - нестабильностью амплитуды и частоты источника переменного напряжения.
Трансформаторные мосты
Типовая схема трансформаторного моста представлена на (рис.10.5). Обмотки трансформатора напряжения Tp1 включают согласовано, а обмотки трансформатора тока Тр2 — встречно. При включенном источнике переменного напряжения Е через Tp1 осуществляется питание моста. За счет токов Ix и Io, протекающих через обмотки w1, w2, w3, w4, на образцовом сопротивлении Zo и измеряемом сопротивлении Zx происходит падение напряжения. Изменяя число витков n3,n4, можно добиться уравновешивания моста, т.е. нулевого показания вольтметра V. Условие равновесия моста: Ixn3 = Ion4. (10.10)
Рисунок 10.5 – Схема трансформаторного моста Учитывая, что
уравнение равновесия моста (10.9) примет вид
Из (10.11) следует, что условие равновесия трансформаторного моста определяется отношением числа витков, на которое не влияют внешние факторы. При постоянном значении образцового сопротивления Zo можно обеспечить широкие пределы измерений за счет изменения количества витков в трансформаторах Tр1 и Тр2. Трансформаторные мосты обеспечивают относительную погрешность в диапазоне звуковых частот 0,001...0,01 %. На основе трансформаторных измерительных мостов реализованы измерители индуктивности (ЕЗ-3) и измерители емкости (Е8-4).
|
|||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 745; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.191.214 (0.021 с.) |


 . (10.1)
. (10.1) (10.2)
(10.2)
 (10.4)
(10.4)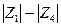 - модули полных сопротивлений плеч; φ1 – φ4 – фазовые сдвиги между током и напряжением в соответствующих плечах.
- модули полных сопротивлений плеч; φ1 – φ4 – фазовые сдвиги между током и напряжением в соответствующих плечах. (10.5)
(10.5) (10.6)
(10.6)


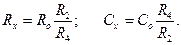 (10.8)
(10.8)


 (10.9)
(10.9)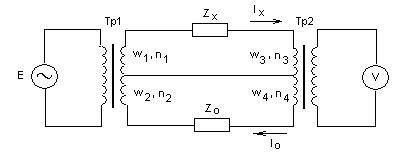

 (10.11)
(10.11)


