Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формирование дискретных lti-объектовСтр 1 из 10Следующая ⇒
ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ В СРЕДЕ MATLAB
Учебное пособие
Самара Самарский государственный технический университет Печатается по решению редакционно-издательского совета СамГТУ
УДК 681.51
Будин В. И. Теория автоматического управления в среде MATLAB: учеб. пособие / В. И. Будин, Ф. В. Дремов. – Самара: Самар. гос. техн. ун-т, 2014. – 127 с.: ил. 36, табл. 7. Библиогр.: 9 назв.
Излагаются функциональные возможности системы MATLAB с ее основными приложениями Control System Toolbox и Simulink, которые ориентированы на решение задач теории автоматического управления. Материал сопровождается значительным количеством примеров. Приводятся контрольные вопросы и упражнения для самостоятельного решения. Для студентов технических вузов всех форм обучения, изучающих дисциплину «Теория автоматического управления» по программам направлений бакалавриата «Автоматизация технологических процессов и производств» и «Электроэнергетика и электротехника (профиль - Электропривод и автоматика промышленных установок)». Может быть также полезно при выполнении выпускных квалификационных работ по данным направлениям.
УДК 681.51 Рецензенты: зам. начальника кафедры АРЭО ВУНЦ ВВС "ВВА" к.т.н. Алексеев Э.О.;
доцент кафедры «Электромеханика и промышленная автоматика» Сф СамГТУ к.т.н. Горшков Р.Г.
Ó В. И. Будин, Ф. В. Дремов, 2014 Ó Самарский государственный технический университет, 2014
ПРЕДИСЛОВИЕ
Предлагаемое учебное пособие написано в соответствии с требованиями Федерального государственного образовательного стандарта для высшего профессионального образования к уровню подготовки бакалавров направлений «Автоматизация технологических процессов и производств» и «Электроэнергетика и электротехника» по дисциплине «Теория автоматического управления» с целью самостоятельного изучения пакета научно-инженерских расчетов MATLAB и его практического применения для решения задач анализа и синтеза автоматических систем, в том числе, освоение способов построения моделей динамических объектов и систем непрерывного и дискретного управления в среде MATLAB, формирование устойчивых навыков использования функций и команд приложений пакета MATLAB для исследования и проектирования систем автоматического управления во временной и частотной областях, освоение методов машинного моделирования нелинейных систем и их параметрическая оптимизация с использованием Simulink.
Данное пособие является дополнением к учебникам по теории автоматического управления и имеет практическую направленность. Особенно оно полезно студентам при выполнении дипломного проекта и курсовых работ, связанных с проектированием автоматических систем. В пособии основной упор делается на получение и закрепление устойчивых навыков применения MATLAB: в каждом разделе приводится большое количество примеров, иллюстрирующих использование функций и команд MATLAB; в практической части каждой темы предлагается самостоятельное выполнение значительного количества заданий; каждая глава заканчивается объемным дополнительным упражнением и контрольными вопросами. Начинать изучение материала пособия целесообразно с первой главы, т.к. он выстроен в соответствии с принципами последовательного перехода от известной информации к новой, от простого материала к более сложному, что позволяет наиболее быстро получить практические навыки даже начинающему пользователю MATLAB, не имеющего опыта работы в этой среде. При этом рекомендуется использовать все версии MATLAB выше 7.1, т.к. интерфейс среды более ранних версий пакета несколько отличается, что может вызвать некоторые затруднения при выполнении заданий и упражнений. ВВЕДЕНИЕ
Развитие теории автоматического управления (ТАУ) в последнее десятилетие показывает, что наиболее эффективные методы анализа и синтеза автоматических систем ориентированы на использование ЭВМ. В инженерной практике среди математических компьютерных систем наибольшее распространение получил пакет MATLAB, который имеет значительное количество специальных приложений (Toolbox) для решения задач исследования и проектирования систем автоматического управления (САУ). Среди них можно особо выделить Control System Toolbox и Simulink. Эти приложения являются основным инструментом специалистов в области машинного анализа и синтеза автоматических систем. В большинстве зарубежных изданий по ТАУ среда MATLAB используется как средство решения сложных с вычислительной точки зрения задач, встречающихся при проектировании САУ, в том числе создание математических моделей объектов и систем в целом, их преобразование, расчет динамических процессов и определение точности в установившихся режимах работы систем регулирования.
Следует отметить, что современная теория автоматического управления, в основе которой лежат математические модели управления в виде матричных дифференциальных уравнений практически не применимы без использования системы MATLAB из-за сложности вычислительных процедур. MATLAB по существу создавался как система научно-инженерных расчетов, ядром которой являются операции над матрицами. Это предопределило аббревиатуру пакета MATrix LABoratory (матричная лаборатория). Поэтому современное направление ТАУ в виде метода пространства состояний в значительной мере опирается на вычислительно-алгоритмическое обеспечение системы MATLAB и указывает в свою очередь пути совершенствования и разработки ее новых приложений. В области автоматизированного проектирования систем автоматического управления в настоящее время наибольшее внимание уделяется созданию в вычислительных средах динамических моделей. Поэтому в предлагаемом пособии в первую очередь рассматривается тема формирования в среде MATLAB типовых математических моделей объектов и систем с помощью приложения Control System Toolbox. Он позволяет создавать модели трех классов: два типа на основе передаточных функций (ПФ) и один на основе стандартной формы уравнений состояния. Все эти объекты однозначно взаимосвязаны, имеют определенные приоритеты и могут использоваться для преобразования структурных схем САУ и анализа динамических и статических свойств разрабатываемых систем управления. В этом разделе рассматриваются также вопросы дискретизации непрерывных моделей, создания моделей с запаздыванием и дискретных систем с амплитудно-импульсной модуляцией. Второй раздел посвящен изучению и приобретению навыков исследования САУ в среде MATLAB. В основном это решение задач по оценке динамических параметров систем регулирования, расчету переходных и весовых характеристик, получению частотных характеристик разомкнутых и замкнутых САУ, в том числе в логарифмическом масштабе. Ранее это считалось сложной трудоемкой рутинной работой. Использование среды MATLAB исключает эту проблему. Приводимые функции и команды приложения Control System Toolbox позволяют значительно упростить решение задач анализа линейных САУ. В третьем разделе рассматриваются вопросы использования Simulink для исследования нелинейных САУ. Это самое объемное приложение MATLAB, которое, по существу, с добавлением ядра MATLAB приобретает свойства самостоятельного пакета, предназначенного для моделирования динамических систем. В его основе лежат принципы визуального программирования, благодаря чему модель САУ набирается в виде схемы, состоящей из отдельных типовых блоков. Такая структура позволяет исследовать динамические свойства автоматических систем сразу по нескольким «физическим» координатам с учетом их ограничений и влияния нелинейностей статистических характеристик отдельных звеньев. В основе вычислительных процессов моделирования в Simulink лежат численные методы интегрирования дифференциальных уравнений в виде разностных схем Рунге-Кутты. В качестве метода интегрирования для неопытного пользователя рекомендуется использовать схему, предлагаемую по умолчанию.
При проектировании САУ полученный регулятор, как правило, требует параметрической настройки по заданному критерию качества. Для решения этой задачи в пакет MATLAB встроено приложение Simulink Response Optimization, которому посвящен четвертый раздел пособия. Этот программный продукт интегрирован с Simulink и по существу построен на использовании его модельной схемы. Настройка осуществляется путем одновременной минимизации перерегулирования и длительности переходного процесса по вычисляемым при поиске оптимума переходным характеристикам путем их вписывания в специальную зону, формируемую по заданным показателям качества. Поиск оптимальных настроек регулятора может осуществляться сразу по нескольким параметрам одновременно. При этом учитывается нестабильность параметров объекта управления и системы в целом. В последнем (пятом) разделе предлагается пример проектирования следящей системы с применением рассмотренных функциональных возможностей приложений пакета MATLAB. При этом синтез управляющего устройства осуществляется с применением методики построения многоконтурных систем с подчиненным регулированием координат. На всех этапах проектирования этой САУ используется среда MATLAB.
1. ФОРМИРОВАНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ С ПОМОЩЬЮ ПАКЕТА CONTROL SYSTEM TOOLBOX Пакет Control System Toolbox предназначен для расчета и исследования линейных систем с постоянными параметрами. При реализации этого пакета использованы принципы объектно-ориентированного программирования. Для линейных стационарных систем введен класс так называемых lti -объектов (linear time invariant object – линейные инвариантные во времени объекты). Этот класс включает в себя три подкласса: подкласс ss – для описания объектов в пространстве состояний и подклассы tf и zpk – для представления объектов в виде передаточных функций (ПФ). Модель системы, заданная в одном из этих подклассов, может быть преобразована в любой другой подкласс. Дополнительные параметры позволяют указать, является ли система непрерывной или дискретной, имеется ли запаздывание на входах системы, задать наименования входов, выходов, переменных состояния, а так же другую вспомогательную информацию о системе.
Формирование tf-объектов
Математическая модель непрерывной системы в форме tf -объекта (transfer function - передаточная функция) имеет следующий вид:
где bi, ai – коэффициенты операторных полиномов соответственно числителя и знаменателя ПФ; s – комплексная переменная; m, n – соответственно порядки числителя и знаменателя ПФ. Для создания (ввода) tf -модели используется функция с одноименным идентификатором:
где num = [b1, b2, …, bm+1], den = [a1, a2, …, an+1] – соответственно массивы коэффициентов числителя и знаменателя ПФ вида (1.1); w – имя созданного объекта (передаточной функции) подкласса tf. По умолчанию сформированные ПФ выводятся на экран в функции переменной s. Пример 1.1. Создание объекта w1 подкласса tf по передаточной функции вида
Сравнивая с формой (1.1), получим
b1=199,54, b2=1585; a1=1,85
В строке ввода команд набирается команда
>>w1=tf([199.54, 1585],[1.85e-6, 3.0854e-3, 1.2874, 1, 0])
Результат отобразится в следующей форме:
Transfer function: 199.5 s + 1585
Задание 1.1. Сформируйте модель h1 tf-подкласса по ПФ вида
Для создания модели статического звена можно использовать команду tf(b1, a1) или tf(k), где k – коэффициент передачи. Пример 1.2. Формирование модели электронного усилителя с коэффициентом передачи W(s)=150.
>> w2=tf(150) Transfer function:
Задание 1.2. Создайте tf-модель h2 для безынерционного объекта с ПФ H2(s)=11,45. Формирование zpk-объектов Математическая модель непрерывной системы в форме zpk -объекта (zero-pole-gain – нули-полюсы-коэффициент) представляет передаточную функцию вида:
где zi и pi – соответственно нули и полюсы ПФ; k – обобщенный коэффициент передачи, связанный с коэффициентом передачи к соотношением:
Для создания zpk -объекта используется функция с одноименным именем:
где k – обобщенный коэффициент передачи; z=[z1, z2, …, zm], p=[p1, p2, …, pn] – соответственно векторы нулей и полюсов ПФ вида (1.2). При этом, если нули или полюсы отсутствуют, то в функцию вместо них вводятся пустые массивы [ ]. Пример 1.3. Формирование zpk -объекта на основе передаточной функции
>> w3=zpk([], [0, -845, -822, -0.7782], 102702.7027) Zero/pole/gain:
s (s+845) (s+822) (s+0.7782)
Задание 1.3. Создайте zpk-объект h3 на основе передаточной функции:
Для формирования zpk -модели безинерционного звена можно использовать функцию zpk в двух формах: стандартный вид zpk ([], [], k) и сокращенный вариант zpk(k), где k - коэффициент передачи. Пример 1.4. Создание zpk -модели статического звена с ПФ W4(s)=75,3. >> w4=zpk(75.3) Zero/pole/gain: 75.3
Задание 1.4. Сформируйте lti-объект h4 подкласса zpk по ПФ H4(s)=0,375.
Формирование ss-объектов
Математическая модель непрерывной системы в форме ss - объекта (state space – пространство состояния) представляется в виде стандартной системы уравнений состояния:
где A, B, C, D – соответственно матрицы состояния, входа, выхода и обхода; X, U, Y – соответственно векторы состояния, входа и выхода. Для формирования ss -объектов предназначена функция:
где a,b,c,d – массивы коэффициентов одноименных матриц (A, B, C, D); sys – имя объекта. Для моделей с нулевой матрицей D (наиболее часто встречающийся вариант) можно использовать присваивание d =0 как краткую форму записи нулевой матрицы соответствующих размеров. Пример 1.5. Формирование ss -модели с именем sys5 для динамического объекта, заданного в пространстве состояний четверкой матриц:
>> sys5=ss([-1668, -679.6; 1024, 0],[8192; 0],[131.70, 102.1], 0)
a = x1 x2 x1 -1668 -679.6 x2 1024 0
b = u1 x1 8192 x2 0
c = x1 x2 y1 131.7 102.1
d = u1 y1 0
Continuous-time model.
Задание 1.5. Создайте ss-модель h5 по математической модели, заданной матрицами:
Модель ss -подкласса удобно использовать для задания матрицы коэффициентов передачи многомерного безынерционного объекта с помощью функции ss(D). Пример 1.6. Построение ss -модели для двухмерного безынерционного объекта, заданного матрицей
>> sys6=ss([3.6 0.5; 1.75 14.3]) d = u1 u2 y1 3.6 0.5 y2 1.75 14.3
Static gain. Задание 1.6. Сформируйте статический объект в виде ss-модели h6 с тремя входами и двумя выходами с матрицей коэффициентов передачи вида
Родовые свойства
Таблица 1.2 Частотные характеристики
В теории и практике систем автоматического управления наибольшее применение находят амплитудно-фазовые частотные характеристики (АФХ или их иногда называют годографами Найквиста), логарифмические частотные характеристики (диаграммы Боде) и амплитудные частотные характеристики. Для их расчета и построения в Control System Toolbox включены соответствующие функции. Построение частотного годографа Найквиста осуществляется с помощью группы функций nyquist:
nyquist(sys), nyquist(sys,dw),
где sys – непрерывная или дискретная lti- модель любого подкласса; dw={Wmin, Wmax} – диапазон частот; Wmin, Wmax – соответственно минимальная и максимальная частоты. Частотный диапазон можно также задать с помощью массива конкретных частот dw=[w1,w2,…,wn], где n – число частот.
Для создания логарифмически распределенного вектора частот используется команда logspaсe. Эта функция возвращает вектор-строку логарифмически возрастающих частот:
logspaсe(log10(Wmin), log10(Wmax)) logspaсe(log10(Wmin), log10(Wmax), N),
где N – число точек в диапазоне частот (по умолчанию N =50).
Основной функцией является nyquist(sys), в которой частотный диапазон определяется автоматически по минимальному и максимальному значениям и массива нулей и полюсов lti -модели. Если последняя содержит астатизм, то выдается предупреждающее сообщение, что на нулевой частоте характеристика равна бесконечности (неопределенное значение). Поэтому в этом случае целесообразно использовать функцию вида nyquist(sys,dw). В практических задачах функция nyquist наиболее часто применяется для построения годографа разомкнутой САУ с целью исследования устойчивости замкнутой системы с помощью критерия Найквиста. Для дискретных систем из-за периодичности частотной характеристики АФХ рассчитывается в диапазоне от нуля до частоты Найквиста ( Пример 2.8. Построение АФХ разомкнутой системы с ПФ W(s) (рис.2.2). >> nyquist(w)
Рис. 2.2. Амплитудно-фазовая характеристика разомкнутой системы Задание 2.8.Постройте годограф Найквиста дискретной САУ по ПФ разомкнутой системы D(z).
Если требуется построить годографы Найквиста для нескольких систем в одних координатах, то можно использовать функцию nyquist в более общих формах:
nyquist(sys1, sys2,…,sysN) nyquist(sys1, sys2,…,sysN, dw) nyquist(sys1, 'plotstyle1',…,sysN, 'plotstyleN'),
где 'plotstyleK' – аргумент, определяющий стиль линии, т.е. цвет и тип годографа K -ой lti -модели. Примечание. Задание стиля осуществляется в соответствии с правилами оформления графиков в MATLAB – в виде набора трех символьных маркеров, заключенных в апострофы. Один из них определяет тип линии (табл. 2.1), другой – цвет (табл. 2.2). При этом можно указывать не все маркеры. В этом случае действуют маркеры, установленные по умолчанию. Порядок маркеров в строке стиля не регламентирован, т.е. может быть произвольным.
Таблица 2.1 Тип линии
Таблица 2.2 Цвет линии
Пример 2.9. Построение АФХ разомкнутой системы соответственно с ПФ W(s) и 0.5W(s) в одних координатах комплексной плоскости с пометкой годографа W(s) маркером 'r-', а годографа 0.5W(s) - маркером ':b' (рис.2.3).
>> nyquist(w,'r-',0.5*w,':b')
Рис. 2.3. Маркированные годографы Найквиста
Задание 2.9.Постройте годографы Найквиста для разомкнутой дискретной системы с ПФ D(z) и 0.7D(z), пометив годограф D(z) маркером ‘-.g’, а годограф 0.7D(z) – маркером ‘m- -‘. Имеются две формы вызова функции nyquist, которые применяются для расчета годографа Найквиста без его построения:
[re,im,w]= nyquist(sys) [re,im,w]= nyquist(sys,dw) где re,im – соответственно векторы значений вещественной и мнимой частей частотной передаточной функции; w – вектор вычисленных частот (при необходимости его можно опустить). Пример 2.10. Расчет значений действительной и мнимой частотных характеристик разомкнутой системы с ПФ W(s) в частотном диапазоне 1 - 30 рад/с.
>> [Re,Im]= nyquist(w,logspace(log10(1),log10(30),5))
Задание 2.10. Вычислите значения параметров АФХ для разомкнутой дискретной системы с ПФ D(z) в диапазоне частот от 0 до π/Тs. Построение логарифмических частотных характеристик (ЛЧХ) осуществляется с помощью функции bode, которая как и функция nyquist имеет несколько форм обращения:
bode(sys) bode(sys,dw) bode (sys1, sys2,…,sysN) bode (sys1, sys2,…,sysN, dw) bode (sys1, 'plotstyle1',…,sysN, 'plotstyleN') [mag, phase, w]= bode(sys)
где sys – непрерывная или дискретная lti -модель; mag, phase, w – соответственно векторы амплитуд, фаз (в градусах) и частот (рад/с). Все команды, кроме последней, осуществляют построение диаграмм Боде, представляющих совокупность двух частотных характеристик в логарифмическом масштабе: логарифмической амплитудно-частотной характеристики (ЛАЧХ) и логарифмической фазо-частотной характеристики (ЛФЧХ). Пример 2.11. Построение логарифмических частотных характеристик для системы, заданной ПФ W(s) (рис.2.4), где команда grid on использована для нанесения сетки на график.
>> bode(w); grid on % Здесь команда grid on использована для % нанесения сетки на график
Рис. 2.4. Логарифмические частотные характеристики системы
Задание 2.11.Постройте диаграмму Боде для разомкнутой дискретной системы с ПФ D(z).
Использование других вариантов функции bode аналогично функции nyquist.
Пример 2.12. Расчет параметров ЛЧХ для разомкнутой системы с ПФ W(s).
>> [Mag12,Phase12,W]=bode(w,[0.5,1,4,8,17])
Mag12(:,:,1) = 12.7870 Mag12(:,:,2) = 3.7365 Mag12(:,:,3) = 0.6285 Mag12(:,:,4) = 0.2531 Mag12(:,:,5) = 0.0974 Phase12(:,:,1) = -146.7687 Phase12(:,:,2) = -139.8197 Phase12(:,:,3) = -141.4908 Phase12(:,:,4) = -167.2469 Phase12(:,:,5) = -214.7002
W = 0.5000 1.0000 4.0000 8.0000 17.0000 Задание 2.12. Постройте таблицу значений амплитуды и фазы от частоты для разомкнутой дискретной системы с ПФ D(z). Очень часто требуется определять запасы устойчивости системы по амплитуде (модулю) и фазе. Из теории автоматического управления известно, что запас устойчивости по модулю равен значению амплитудной частотной характеристики (АЧХ) на частоте Wc, при которой фазовая частотная характеристика (ФЧХ) имеет значение -1800, а запас по фазе – значение разности между ФЧХ и - 1800 на частоте среза Wcр. Для определения этих параметров используется функция margin:
margin(sys) [Gm, Pm, Wc, Wcp]= margin(sys)
Здесь sys – непрерывная или дискретная lti -модель;
Gm – запас по модулю на частоте Wc; Pm – запас по фазе на частоте среза Wcp.
Команда margin(sys) строит диаграмму Боде с указанием запасов устойчивости, а функция [Gm, Pm, Wc, Wcp]=margin(sys) рассчитывает значения Gm, Pm, Wc и Wcp без построения логарифмических частотных характеристик. Пример 2.13. Определение запасов устойчивости непрерывной системы с ПФ разомкнутой системы W(s) (рис. 2.5). >> margin(w)
Рис. 2.5. Диаграмма Боде, построенная с помощью функций margin Задание 2.13.Рассчитайте значения запасов устойчивости по модулю и фазе дискретной системы с ПФ разомкнутой системы D(z) без построения ЛЧХ. При проектировании САУ часто используется показатель колебательности, который определяется в виде отношения максимального значения модуля частотной характеристики замкнутой системы к его величине на нулевой частоте (коэффициенту передачи системы). Максимальное значение модуля частотной характеристики связано с нормой типа - для непрерывных систем соотношением
- для дискретных систем - соотношением
В связи с этим была составлена и включена в пакет Control System Toolbox функция norm в следующих формах:
normsys = norm(sys, inf) normsys = norm(sys, inf, tol) [ninf, fpeak]= norm(sys, inf),
где normsys – максимальное значение АЧХ lti-модели sys; inf – идентификатор нормы tol – точность расчета нормы (по умолчанию tol =1е-2); ninf - максимальное значение модуля частной характеристики на частоте fpeak. При этом необходимо учитывать, что если объект sys имеет астатизм, то максимальное значение модуля АЧХ равно бесконечности.
Пример 2.14. Расчет максимального значения АЧХ динамической системы с ПФ замкнутой системы Ф(s). >> [Am, Fm]=norm(f, inf) Am = 13.7209 Fm = 1.7976 Задание 2.14. Определите значение показателя колебательности дискретной САУ с ПФ замкнутой системы Т(z), учитывая, что ее коэффициент передачи равен единице.
Временные характеристики
Для исследования динамических свойств систем автоматического управления часто используются типовые переходные режимы работы (временные характеристики). Наибольшее применение находят следующие временные характеристики: · переходная функция (характеристика) – реакция системы на единичный скачкообразный сигнал при нулевых начальных условиях; · весовая функция (импульсная переходная характеристика) – реакция непрерывной системы на воздействие в виде δ -импульса Дирака, а для дискретной системы – на единичный импульс. · реакция системы на ненулевые начальные условия. По временным характеристикам можно определить ряд качественных показателей, характеризующих динамические свойства системы управления, в частности, перерегулирование, время переходного процесса и др. В пакете Control System Toolbox имеется ряд функций для расчета и построения временных характеристик линейных систем. Основными из них являются step, impulse, initial. Функция step вычисляет и отображает на экране переходную характеристику lti -модели. Она имеет несколько форм: step (sys) step (sys,t) step (sys1, sys2,…,sysN) step (sys1, sys2,…,sysN, t) step (sys1, 'plotstyle1',…,sysN, 'plotstyleN') step (sys1, 'plotstyle1',…,sysN, 'plotstyleN', t).
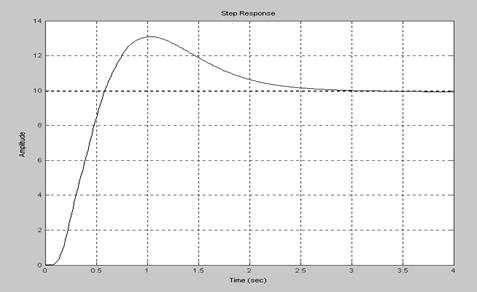
Здесь t – аргумент, задающий время моделирования в виде длительности переходного режима t=Tfinal (в секундах) или в виде вектора t=0:dt:Tfinal. Для дискретных моделей dt=Ts, а для непрерывных выбирается достаточно малым для учета быстрых изменений переходного процесса. Продолжительность моделирования при отсутствии аргумента t определяется автоматически. Остальные параметры функции step такие же, как в функциях nyquist и bode. Пример 2.15. Построение переходной характеристики для непрерывной САУ с ПФ Ф(s) (рис.2.6). >> step(f); grid on
Рис. 2.6. Переходная характеристика
Задание 2.15.Постройте переходную функцию для дискретной САУ, заданной передаточной функцией замкнутой системы Т(z). Для расчета переходной характеристики без ее построения используются две дополнительные формы функции step:
[y, t, x]= step(sys) [y, t, x]= step(sys, t)
В этом случае функция step возвращает векторы значений выхода y, времени t и переменных состояния х (количество столбцов вектора х равно размерности lti -модели). Если модель представлена в tf или zpk формах, то параметр х опускается. Пример 2.16. Расчет переходной характеристики с шагом 0.2 с без ее построения для непрерывной САУ с ПФ замкнутой системы Ф(s). >> [y,t]=step(f,[0:0.2:4])
Задание 2.16. Произведите вычисление переходной функции дискретной системы с ПФ замкнутой САУ T(z) без ее построения.
Для расчета и построения импульсной переходной (весовой) характеристики используется функция impulse в таких же формах, как и функция step:
impulse (sys) impulse (sys,t) impulse (sys1, sys2,…,sysN) impulse (sys1, sys2,…,sysN, t) impulse (sys1, 'plotstyle1',…,sysN, 'plotstyleN') impulse (sys1, 'plotstyle1',…,sysN, 'plotstyleN', t) [y, t, x]= impulse (sys) [y, t, x]= impulse (sys, t)
Пример 2.17. Построение весовой характеристики для линейной непрерывной САУ с ПФ замкнутой системы Ф(s) (рис. 2.7). >>impulse(f); grid on
Рис. 2.7. Весовая характеристика
Задание 2.17.Постройте импульсную переходную характеристику для дискретной системы с ПФ замкнутой САУ Т(z).
Функция initial рассчитывает и строит график реакции ss -модели sys на ненулевые начальные условия. Она имеет несколько форм, эквивалентных функциям step и impulse:
initial (sys,х0) initial (sys,х0,t) initial (sys1, sys2,…,sysN,х0) initial (sys1, sys2,…,sysN,х0, t) [y, t, x]= initial (sys,х0) [y, t, x]= initial (sys,х0, t)
Здесь х0 – вектор начальных условий lti -модели в пространстве состояний. Смысл остальных аргументов и возвращаемых величин такой же, как у функций step и impulse.
Пример 2.18. Построение реакции непрерывной системы, заданной математической моделью в пространстве состояний на единичное начальное условие по последней переменной состояния, т.е. х(0)=|0 0 0 0 0 0 1 | (рис. 2.8).
>> sys 18=ss(f); x0=[0 0 0 0 0 0 1];initial(sys 18,x0); grid on
Рис. 2.8. Реакция по переменной состояния
Задание 2.18.Постройте график реакции дискретной системы с исходной ПФ T(z) и представленной ss-моделью на единичное начальное условие по второй переменной состояния х(0)=|0 1 0 0 0 0 0|. К блоку временных функций пакета Control System Toolbox относится еще две функции: lsim – вычисление переходного процесса при произвольном входном воздействии, который формируется с помощью функции gensig – генерация периодического сигнала заданного типа (синусоида, импульсная последовательность и прямоугольный периодический сигнал). Однако на практике они используются редко, так как для моделирования систем при сложных воздействиях более удобен пакет Simulink. Дополнительное упражнение
1.Открыть mat -файл из созданного в результате выполнения дополнительного задания в разделе 1. 2.Используя lti -модели, полученные для разомкнутой и замкнутой непрерывной САУ, выполнить следующие виды работ. 2.1. Определить полюсы и нули замкнутой системы. 2.2. Осуществить сортировку полюсов и нулей. 2.3. Построить схему расположения нулей и полюсов на комплексной плоскости. 2.4. Произвести расчет собственных частот и коэффициентов демпфирования замкнутой системы. 2.5. Построить годограф Найквиста разомкнутой системы и оценить по нему устойчивость замкнутой системы. 2.6. Построить ЛЧХ разомкнутой системы и оценить запас устойчивости по фазе. 2.7. Определить запас устойчивости по модулю. 2.8. Рассчитать показатель колебательности системы. 2.9. Построить переходную характеристику системы. 2.10. Построить весовую характеристику системы. 3. Повторить пункты 2.1 ÷ 2.10 для дискретного варианта САУ. Контрольные вопросы 1.Назовите основные функции, которые используются для анализа динамических параметров lti -моделей? 2.Поясните действие функций esort и dsort? 3.С помощью каких функций можно определить полюсы и нули динамической системы? 4.Какие основные функции используются для расчета и построения временных характеристик? 5.Каким образом рассчитываются временные характеристики без их построения? 6.Как задается время расчета переходного процесса? 7.Какие функции служат для построения частотных характеристик динамических систем? 8.Как реализовать логарифмическое изменения частоты? 9.Дайте сравнительную оценку функциям nyquist и bode. 10. С помощью какой функции строится схема расположения нулей и полюсов на комплексной плоскости? 11. Поясните особенности форм обращения к функции damp. 12. Как определить коэффициент передачи системы? 13. С помощью какой функции можно оценить запас устойчивости САУ? 14. Как рассчитать показатель колебательности системы? 15. Поясните особенности использования функции initial и задания в ней начальных условий.
Запуск SIMULINK
Запуск приложения SIMULINK осуществляется в среде MATLAB двумя основными способами: - нажатием кнопки Simulink на панели инструментов основного окна MATLAB; - выполнением команды Simulink в командной строке MATLAB. В результате открывается окно обозревателя (браузера) библиотеки Simulink Library Browser (рис. 3.1).
!! Запустите SIMULINK одним из выше приведенных способов. Для закрытия приложения SIMULINK достаточно через меню окна браузера подать команду File/Close или щелкнуть мышкой на кнопке управления окном обозревателя
!! Закройте приложение SIMULINK. Имеются еще две дополнительные возможности активизации системы SIMULINK. Первая из них связана с запуском созданного ранее MDL-файла, в результате чего появляется одноименное окно S-модели. Далее для вызова обозревателя библиотеки SIMULINK на панели инструментов этого окна нажимается кнопка Library Browser или в меню окна S-модели выбирается опция View/Library Browser.
Рис. 3.1. Окно браузера библиотеки SIMULINK 6
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 877; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.168.56 (0.334 с.) |
 (1.1)
(1.1) ,
, .
. , a2=3,0854
, a2=3,0854  , a3=1,2874, a4 =1, a5= 0.
, a3=1,2874, a4 =1, a5= 0. 1.85e-006 s^4 + 0.003085 s^3 + 1.287 s^2 + s
1.85e-006 s^4 + 0.003085 s^3 + 1.287 s^2 + s

 (1.2)
(1.2) .
. ,
,
 102702.7027
102702.7027 .
. (1.3а)
(1.3а) (1.3б)
(1.3б) ,
,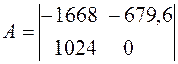 ;
; 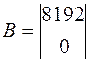 ;
; ;
; 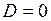 .
. ;
; 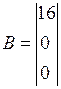 ;
; 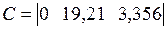 ;
;  .
.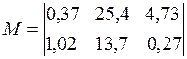 .
. ). Если период Ts неспецифицирован, то по умолчанию принимается Ts = 1.
). Если период Ts неспецифицирован, то по умолчанию принимается Ts = 1.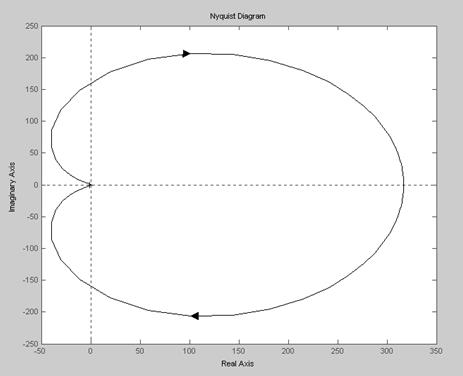








 (Close).
(Close).