Задача о назначениях и венгерский метод ее решения.

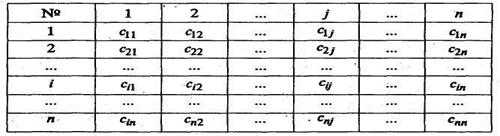
Для решения задачи о назначениях составляют таблицу (табл. 3.6.1):

Таблица 3.6.1

В левой колонке записаны номера кандидатов, в верхней строке – номера работ. В -й строке -мстолбце стоят затраты на выполнение -м кандидатом -й работы.

В венгерском методе используется следующий принцип: оптимальность решения задачи о назначениях не нарушается при уменьшении (увеличении) элементов строки (столбца) на одну и ту же величину. Решение считается оптимальным, если все измененные таким образом затраты , (; ) и можно отыскать такой набор , что

Алгоритм метода содержит следующие шаги.

Шаг 1. Получение нулей в каждой сроке. Для этого в каждой строке определяют наименьший элемент, и его значение отнимают от всех элементов этой строки. Переход к шагу 2.

Шаг 2. Получение нулей в каждом столбце. В преобразованной таблице в каждом столбце определяют минимальный элемент, и его значение вычитают из всех элементов этого столбца. Переход к шагу 3.

Шаг 3. Поиск оптимального решения. Просматривают строку, содержащую наименьшее число нулей. Отмечают один из нулей этой строки и зачеркивают все остальные нули этой строки и того столбца, в котором находится отмеченный нуль. Аналогичные опе­рации последовательно проводят для всех строк. Если назначение, которое получено при всех отмеченных нулях, является полным (т.е. число отмеченных нулей равно ), то решение является опти­мальным, в противном случае следует переходить к шагу 4.

Шаг 4. Поиск минимального набора строк и столбцов, содержащих все нули.

Для этого необходимо отметить:

1) все строки, в которых не имеется ни одного отмеченного нуля;

2) все столбцы, содержащие перечеркнутый нуль хотя бы в одной из отмеченных строк;

3) все строки, содержащие отмеченные нули хотя бы в одном из отмеченных столбцов.

Действия 2) и 3) повторяются поочередно до тех пор, пока есть что отмечать. После этого необходимо зачеркнуть каждую непомеченную строку и каждый помеченный столбец.

Цель этого шага – провести минимальное число горизонтальных и вертикальных прямых, пересекающих по крайней мере один раз все нули.

Шаг 5. Перестановка некоторых нулей.

Взять наименьшее число из тех клеток, через которые проведены прямые. Вычесть его из каждого числа, стоящего в невычеркнутых столбцах и прибавить к каждому числу, стоящему в вычеркнутых строках. Эта операция не изменяет оптимального решения, после чего весь цикл расчета повторить, начиная с шага 3.

Задача о рюкзаке.

Задача о загрузке (задача о рюкзаке) и различные её модификации широко применяются на практике в прикладной математике, криптографии, экономике, логистике, для нахождения решения оптимальной загрузки различных транспортных средств: самолетов, кораблей, железнодорожных вагонов и т.д. Задача о ранце – одна из задач комбинаторной оптимизации. Классическая задача о ранце известна очень давно. Вот её постановка: Имеется набор из N предметов, каждый предмет имеет массу Wi и полезность Vi, i=(1,2..N), требуется собрать набор с максимальной полезностью таким образом, чтобы он имел вес не больше W, где W – вместимость ранца.

Пример: Задание. В рюкзак объема V = 7 кладут N = 5 предметов.Объемы, веса и количество предметов в каждой группе приведены в таблице.

Объем
Вес
Кол-во

 

Максимизировать общий вес рюкзака.

Решение.

I этап. Условная оптимизация.
f₁(L) = max(2x₁); 0 < x₁ < 1; x₁ = 0,1.
f₁(0) = max[0*2] = 0
f₁(1) = max[0*2, 1*2] = 2
f₁(2) = max[0*2, 1*2] = 2
f₁(3) = max[0*2, 1*2] = 2
f₁(4) = max[0*2, 1*2] = 2
f₁(5) = max[0*2, 1*2] = 2
f₁(6) = max[0*2, 1*2] = 2
f₁(7) = max[0*2, 1*2] = 2

Таблица 1 – Расчет значения функции f₁(L)

L
f1(L)
x1

f₂(L) = max[3x₂ + f₁(L - 2x₂)]; 0 < x₂ < 3; x₂ = 0,1,2,3.
f₂(0) = max[0*3+0] = 0
f₂(1) = max[0*3+2] = 2
f₂(2) = max[0*3+2, 1*3+0] = 3
f₂(3) = max[0*3+2, 1*3+2] = 5
f₂(4) = max[0*3+2, 1*3+2, 2*3+0] = 6
f₂(5) = max[0*3+2, 1*3+2, 2*3+2] = 8
f₂(6) = max[0*3+2, 1*3+2, 2*3+2, 3*3+0] = 9
f₂(7) = max[0*3+2, 1*3+2, 2*3+2, 3*3+2] = 11
Таблица 2 – Расчет значения функции f₂(L)

 

L
f2(L)
x2

 

f₃(L) = max[2x₃ + f₂(L - 3x₃)]; 0 < x₃ < 3; x₃ = 0,1,2,3.
f₃(0) = max[0*2+0] = 0
f₃(1) = max[0*2+2] = 2
f₃(2) = max[0*2+3] = 3
f₃(3) = max[0*2+5, 1*2+0] = 5
f₃(4) = max[0*2+6, 1*2+2] = 6
f₃(5) = max[0*2+8, 1*2+3] = 8
f₃(6) = max[0*2+9, 1*2+5, 2*2+0] = 9
f₃(7) = max[0*2+11, 1*2+6, 2*2+2] = 11
Таблица 3 – Расчет значения функции f₃(L)

L
f3(L)
x3

f₄(L) = max[4x₄ + f₃(L - 1x₄)]; 0 < x₄ < 1; x₄ = 0,1.
f₄(0) = max[0*4+0] = 0
f₄(1) = max[0*4+2, 1*4+0] = 4
f₄(2) = max[0*4+3, 1*4+2] = 6
f₄(3) = max[0*4+5, 1*4+3] = 7
f₄(4) = max[0*4+6, 1*4+5] = 9
f₄(5) = max[0*4+8, 1*4+6] = 10
f₄(6) = max[0*4+9, 1*4+8] = 12
f₄(7) = max[0*4+11, 1*4+9] = 13
Таблица 4 – Расчет значения функции f₄(L)

L
f4(L)
x4

f₅(L) = max[1x₅ + f₄(L - 1x₅)]; 0 < x₅ < 2; x₅ = 0,1,2.
f₅(0) = max[0*1+0] = 0
f₅(1) = max[0*1+4, 1*1+0] = 4
f₅(2) = max[0*1+6, 1*1+4, 2*1+0] = 6
f₅(3) = max[0*1+7, 1*1+6, 2*1+4] = 7
f₅(4) = max[0*1+9, 1*1+7, 2*1+6] = 9
f₅(5) = max[0*1+10, 1*1+9, 2*1+7] = 10
f₅(6) = max[0*1+12, 1*1+10, 2*1+9] = 12
f₅(7) = max[0*1+13, 1*1+12, 2*1+10] = 13
Таблица 5 – Расчет значения функции f₅(L)

L
f5(L)
x5

II этап. Безусловная оптимизация.
Таким образом, максимальный вес рюкзака f₅(7) равна 13 кг.
При этом x₅ = 0, так как f₅(7) = 13 достигается при х₅=0 (см. таблицу 5).
Предметы остальных типов распределяются следующим образом:
L = 7 - 1 * 0 = 7
f₄(7) = 13 достигается при х₄ = 1 (см. таблицу 4).
L = 7 - 1 * 1 = 6
f₃(6) = 9 достигается при х₃ = 0 (см. таблицу 3).
L = 6 - 3 * 0 = 6
f₂(6) = 9 достигается при х₂ = 3 (см. таблицу 2).
L = 6 - 2 * 3 = 0
f₁(0) = 0 достигается при х₁ = 0 (см. таблицу 1).
L = 0 - 1 * 0 = 0
В итоге наилучший вариант загрузки рюкзака достигается при значениях: x₁ = 0, x₂ = 3, x₃ = 0, x₄ = 1, x₅ = 0

Задача оптимального раскроя

Рассмотрим задачу оптимального линейного раскроя.

Есть достаточно большое число одномерных заготовок одинаковой длины D = 2,6 м. Заготовки следует разрезать на детали 3 типов длиной L = (1,5; 0,9; 1,2). По данным числам D и L_i составить матрицу всех возможных способов раскроя A = a_ij, где каждое a_ij указывает количество деталей i типа, что выходит из одной заготовки при раскрое по j способому, если заданы также потребности B = (45, 74, 66), в деталях i типа.
Составить математическую модель и решить задачу линейного программирования для выполнения планового задания, раскроив минимальное число заготовок.

Решение

Составим таблицу исходных данных:

i	Li	Bi
	1,5
	0,9
	1,2

Заполним матрицу всех возможных способов раскроя, учтя длину заготовок D = 2,6 м:

Длина раскроев	Способы раскроя
1	2	3	4
1,5
0,9
1,2

Таким образом, матрица A следующая:

Получим задачу целочисленного линейного программирования:

z = x ₁ + x ₂ + x ₃ + x ₄ → min

x ₁, x ₂, x ₃, x ₄ > 0

1) Первый этап

Найдем решение, отбросив условие целочисленности. Изменим знаки целевой функции на противоположные и будем рассматривать задачу на максимум:
z = - x ₁ - x ₂ - x ₃ - x ₄ → max

Сведем задачу к каноническому виду, для чего прибавим дополнительные или базисные векторы [АКУ, с. 12]:

Для увеличения количества базисных векторов отнимаем от строки, которая содержит отрицательную вспомогательную переменную и максимальный B ₂ = 74 все строки с отрицательными вспомогательными переменными (1, 3) [ГЕТ, с. 177].

Поскольку начальный план нельзя построить обычным образом, используем метод искусственного базиса [АКУ, с. 47].
Вектор z ₁ является искусственным.

Тогда целевая функция запишется так:

z = - x ₁ - x ₂ - x ₃ - x ₄ – Mz ₁ → max,

где M - большое число.

Построим начальную симплекс-таблицу, где
Q - неотрицательное отношение столбца плана к ключевому столбцу.

№

Базис

Cб

План

-1

-1

-1

-1

- M

Q

x 1

x 2

x 3

x 4

x 5

x 6

x 7

z 1

x 5

-1

29/2

z 1

- M

-1

x 7

-2

-1

Δ j

–

-74

-1

-2

-1

–

Cтолбик 2 есть ключевым, поскольку он содержит минимальный отрицательный элемент

Δ₂ = -2 M + 1.

Строка 3 есть ключевой, поскольку в ней минимальное Q ₃ = 4.
Ключевой элемент находится на их пересечении и равный числу 2.
Вместо вектора x ₇, который удаляем из базиса, вводим вектор x ₂.
Делим ключевую строку на ключевой элемент 2.
Умножаем его на -1 и добавляем к 4 строке.
Умножаем его на -2 и добавляем к 1 строке.
Умножаем его на -2 и добавляем к 2 строке.
Получим следующую симплекс-таблицу.

№

Базис

Cб

План

-1

-1

-1

-1

- M

Q

x 1

x 2

x 3

x 4

x 5

x 6

x 7

z 1

x 5

-1

-1

21/2

z 1

- M

-1

x 2

-1

1/2

-1

-1/2

1/2

–

Δ j

-4

1/2

1/2

-1/2

–

-66

-1

-2

–

Cтолбик 4 есть ключевым, поскольку он содержит минимальный отрицательный элемент Δ₄ = -2 M + 2.

Строка 1 есть ключевой, поскольку в ней минимальное Q ₁ = 21/2.
Ключевой элемент находится на их пересечении и равный числу 2.
Вместо вектора x ₅, который удаляем из базиса, вводим вектор x ₄.
Делим ключевую строку на ключевой элемент 2.
Умножаем его на -2 и добавляем к 4 строке.
Умножаем его на -2 и добавляем к 2 строке.
Умножаем его на 1 и добавляем к 3 строке.
Получим следующую симплекс-таблицу.

№

Базис

Cб

План

-1

-1

-1

-1

- M

Q

x 1

x 2

x 3

x 4

x 5

x 6

x 7

z 1

x 4

-1

21/2

-1/2

1/2

1/2

-1/2

–

z 1

- M

-1

x 2

-1

29/2

1/2

1/2

-1/2

–

Δ j

-25

3/2

-1

1/2

1/2

–

-45

-1

–

Cтолбик 1 есть ключевым, поскольку он содержит минимальный отрицательный элемент Δ₁ = - M + 3/2.
Строка 2 есть ключевой, поскольку в ней минимальное Q ₂ = 45.
Ключевой элемент находится на их пересечении и равный числу 1.
Вместо вектора z ₁, который удаляем из базиса, вводим вектор x ₁. Дальше из расчетов данную искусственную переменную исключаем.
Делим ключевую строку на ключевой элемент 1.
Умножаем его на -3/2 и добавляем к 4 строке.
Умножаем его на 1/2 и добавляем к 1 строке.
Получим следующую симплекс-таблицу.

№	Базис	Cб	План	-1	-1	-1	-1				Q
x 1	x 2	x 3	x 4	x 5	x 6	x 7
	x 4	-1				1/2				-1/2
	x 1	-1						-1			–
	x 2	-1	29/2			1/2		1/2	-1/2
	Δ j	-185/2					1/2	1/2	1/2	–

Поскольку содержится нуль в небазисном векторе x ₃, то существует еще одно оптимальное решение, которое также найдем. Строка 3 есть ключевой, поскольку в ней минимальное Q ₃ = 29.
Ключевой элемент находится на их пересечении и равный числу 1/2.
Вместо вектора x ₂, который удаляем из базиса, вводим вектор x ₃.
Делим ключевую строку на ключевой элемент 1/2.
Умножаем его на -1/2 и добавляем к 1 строке.
Получим окончательную симплекс-таблицу.

№	Базис	Cб	План	-1	-1	-1	-1
x 1	x 2	x 3	x 4	x 5	x 6	x 7
	x 4	-1	37/2		-1			-1/2	1/2	-1/2
	x 1	-1						-1
	x 3	-1							-1
	Δ j	-185/2					1/2	1/2	1/2

Последняя строка таблицы не содержит отрицательных элементов, следовательно найденное решение является оптимальным: X = (45, 0, 29, 37/2), z_max = -185/2.
Вернувшись к замене знака функции, получим: z_min = 185/2.

Решение имеет дробные значения, поэтому переходим ко 2 этапу.

2) Второй этап

Применим метод Гомори для поиска целочисленного решения [АКУ, с. 180].
Дополнительные ограничения строятся по формуле на основании строки,
переменная плана которого имеет наибольшую дробную часть.
Вычислим дробные части основных переменных плана: f ₁(x ₄) = 0,5000.
Неравенство строим на основании 1 строки




Добавляем уравнение к системе уравнений и строим симплекс-таблицу с новым ограничением.
Новую задачу решаем двойственным симплекс-методом [АКУ, с. 107].

№	Базис	Cб	План	-1	-1	-1	-1
x 1	x 2	x 3	x 4	x 5	x 6	x 7	x 8
	x 4	-1	37/2		-1			-1/2	1/2	-1/2
	x 1	-1						-1
	x 3	-1							-1
	x 8		-1/2					-1/2	-1/2	-1/2
	Δ j	185/2					1/2	1/2	1/2

Строка 4 является ключевой, поскольку она содержит минимальный элемент плана: x ₈ = -1/2.
Cтолбик 5 является ключевым, поскольку в нем минимальное двойственное отношение:
Ключевой элемент находится на их пересечении и равен числу -1/2.
Выполняем преобразование таблицы симплексным методом.
Вместо вектора x ₈, который удаляем из базиса, вводим вектор x ₅.
Делим ключевую строку на ключевой элемент -1/2.
Умножаем его на -1/2 и добавляем к 5 строке.
Умножаем его на 1/2 и добавляем к 1 строке.
Умножаем его на 1 и добавляем к 2 строке.
Умножаем его на -1 и добавляем к 3 строке.
Поскольку отрицательного числа в плановом столбце не существует, получим окончательный план.
Занесем его в симплекс-таблицу.

№	Базис	Cб	План	-1	-1	-1	-1
x 1	x 2	x 3	x 4	x 5	x 6	x 7	x 8
	x 4	-1			-1						-1
	x 1	-1									-1
	x 3	-1							-2	-1
	x 5										-2
	Δ j	-93

Поскольку базисные переменные приобрели целые значения, то задача решена.
Последняя строка таблицы не содержит отрицательных элементов, следовательно найденное решение является оптимальным: X = (46, 0, 28, 19), z_max = -93.
Вернувшись к замене знака функции, получим: z_min = 93.
Таким образом, для использования минимального количества заготовок необходимо 1 способом разрезать 46, 3 способом - 28 и 4 способом - 19 заготовок.

Ответ: X = (46, 0, 28, 19), z_min = 93.