
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аппроксимация эмпирических данных линейной зависимостьюСтр 1 из 2Следующая ⇒
КУРСОВАЯ РАБОТА
_________________________________________________________________________ (наименование учебной дисциплины согласно учебному плану)
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
_________________________________________________________________________ _________________________________________________________________________
Автор: студент гр. ГМ-10-1 ____________________ / Богославский Н. А. / (подпись) (Ф.И.О.)
ОЦЕНКА: _____________
Дата: ___________________
ПРОВЕРИЛ
Руководитель проекта ст. преп. ________________ / Кондрашев А. П. / (должность) (подпись) (Ф.И.О.)
Санкт-Петербург 2011 год
Кафедра Информатики и компьютерных технологий ____
КУРСОВАЯ РАБОТА
По дисциплине ___________________________________________________________ _________________________________________________________________________ (наименование учебной дисциплины согласно учебному плану) ЗАДАНИЕ
Студенту группы ГМ-10-1Богославский Н. А. (шифр группы) (Ф.И.О.)
__________________________________________________________________________________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Руководитель проекта ст. преп. ________________ / Кондрашев А. П. / (должность) (подпись) (Ф.И.О.) Дата выдачи задания: 15 сентября 2011г.
Аннотация Курсовая работа содержит расчеты, относящиеся к аппроксимации функциональной зависимости момента нагрузки М [кг·м] исполнительного органа угольного комбайна от толщины среза h [см] методом наименьших квадратов. В работе использовались средства MS Office: Microsoft Exel и Microsoft Word; расчеты проводились в Turbo Pascal, MathCAD. Курсовая работа содержит 35 страниц, 1 таблицу, 2 блок-схемы, 6 рисунка.
The Summary
Term paper contains calculations, related to approximations of functional dependence of the expense load torque M of the executive body of the coal shearer slice thickness h, by a least-squares method.. In it questions of construction of empirical formulas by a method of the least squares with elements of calculations in MathCAD and in programming language Turbo Pascal are considered. Approximating dependences are as a result received Term paper contains 35 pages, 1 table, 2 flow-charts, 6 pictures.
Оглавление Введение. 5 Решение в MS Excel 8 Аппроксимация эмпирических данных линейной зависимостью.. 8 Аппроксимация эмпирических данных квадратичной зависимостью.. 9 Элементы теории корреляции. 10 Решение задачи в Mathcad. 11 Аппроксимация линейной функцей. 11 Аппроксимация квадратичной функции. 13 Вычисление коэффициента детерминированности. 15 Решение задачи в среде Turbo Pascal 19 Описание программы.. 21 Решение СЛАУ методом Гаусса. 22 Вывод. 24 Библиографический список. 25 Приложение 1. 26 Приложение 2. 27 Приложение 3. 28 Приложение 4. 31 Приложение 5. 34
Введение Часто при анализе фактических результатов измерений или экспериментов возникает необходимость найти в явном виде функциональную зависимость между полученными фактическими величинами. Для нахождения аналитической взаимосвязи между двумя величинами M и h производят ряд наблюдений; в результате получается таблица измеренных значений. Поскольку табличные результаты получаются как итог каких-либо экспериментов, эти значения называются эмпирическими или опытными значениями. Таким образом, исходными данными являются два одномерных массива одинаковой длины, содержащие эмпирические данные.
Если между величинами M и h существует некоторая функциональная зависимость, но ее аналитический вид неизвестен, то возникает практическая задача - найти эмпирическую формулу
где Вид функции и значения коэффициентов Нахождение аналитической зависимости между эмпирическими величинами называется аппроксимацией функции заданной таблично. При аппроксимации указывают класс функции, из которой выбирается теоретическая функция (например: линейная или кубическая и т.п.) и далее определяются наилучшие значения коэффициентов с помощью аппроксимации В курсовой работе рассматриваются методы по составлению вычислительных алгоритмов и программ в своей основной специальности “Горно-транспортные машины и оборудование”. Исходные данные заданы в виде двух одномерных табличных массивов. Таблица представляет собой итог экспериментально полученных величин, в результате работы исполнительного органа угольного комбайна, называемых эмпирическими. Горный (угольный) комбайн- комбинированная машина для одновременного выполнения операций по отделению от массива полезного ископаемого или породы и погрузки их на транспортные средства. Горный комбайн, предназначенный для добывания полезного ископаемого, называется очистным, а применяемый для проведения горных выработок- проходческим. Горный комбайн для проведения нарезных выработок по углю в целях подготовки очистного забоя называется нарезным. Наибольшее распространение горный комбайн получил в угольной промышленности. Горный комбайн (Рис. 1.) состоит из исполнительного органа (для отбойки, разрушения массива горных пород), погрузочного органа, роль которого в ряде случаев выполняет тот же исполнительный орган (для погрузки отбитой горной массы на транспорт), механизма передвижения, приводных двигателей, передаточных механизмов, органов управления и устройств для пылеподавления (оросительные системы) и пылеулавливания.
Рис. 1. Очистной комбайн узкозахватный типа с барабанным исполнительным органом для выемки пологих пластов. По конструкции и способу отделения горной массы различают несколько типов исполнительных органов горных комбайнов: · баровые, состоящие из одного или нескольких баров с режущими цепями, разрушающих массив системой зарубных щелей с последующим разрушением межщелевых целиков либо резанием с поверхности забоя · шнековые (с горизонтальной осью вращения), разрушающие массив резанием с поверхности забоя и перемещающие вдоль оси шнека отдельные куски горной массы на конвейер · буровые, разрушающие массив вырезанием концентрических тонких кольцевых щелей с последующим разрушением и погрузкой на конвейер межщелевых целиков · шарошечные, разрушающие массив системой шарошек Исполнительный орган горного комбайна в ряде случаев может быть комбинированным (например, буровой и барабанный, планетарный и шнековый).
При проведении испытаний исполнительного органа угольного комбайна получена следующая зависимость момента нагрузки М от толщины среза h. Таблица 1 Зависимость момента нагрузки М [кг·м] исполнительного органа угольного комбайна от толщины среза h [см].
Построим график для выбора функций, с помощью которых будет производиться аппроксимация этой зависимости.
Рис. 2. График зависимости таблично заданных значений M и h. График зависимости, построенный по значениям табл.1 показывает, что для аппроксимации можно выбрать линейную и квадратичную функции. Решение в MS Excel Элементы теории корреляции Коэффициент корреляции является мерой линейной связи между зависимыми величинами. Он показывает, насколько хорошо, в среднем, может быть представлена (вычислена) одна из величин в виде линейной функции от другой. Коэффициент корреляции вычисляется по формуле:
где Коэффициент корреляции по абсолютной величине не превосходит 1. Чем ближе Особо подчеркнем, что если коэффициент корреляции существенно меньше 1, это не означает отсутствие зависимости между параметрами h и M. Это означает только, что не применима линейная аппроксимация, но можно искать аппроксимирующую зависимость среди степенных, экспоненциальных, квадратичных и других классов функций. Расчет коэффициента корреляции r в Mathcad, выдал результат: r=0.964846<1. Исходя из этого можно сделать вывод, что применима линейная аппроксимация между случайными величинами h и M. Следовательно, выбор линейной функции для аппроксимации был сделан верно. Решение задачи в Mathcad Описание программы Рассмотрим наиболее важные функции и процедуры, используемые для вычисления сумм (элементов матрицы коэффициентов) квадратичной функции: Процедура ASSIGN используется для связывания файловой переменной с именем файла. В общем виде записывается следующим образом: ASSIGN (<файловая переменная>, <имя файла или логическое устройство>);
Конкретно в курсовой работе процедура ASSIGN представлена в следующем виде: assign(fw,'gaus.txt'); assign(fm,kursovik.txt'); На языке Turbo Pascal имеются три различных оператора, с помощью которых можно запрограммировать повторяющиеся фрагменты программ. В данной программе используется счётный оператор цикла FOR., который используется для вычисления сумм всех чисел от 1 до n. В общем виде записывается следующим образом: FOR <параметр_цикла>:= <начальное_значение> ТО <конечное_значение> DO <оператор> FOR, TO, DO - зарезервированные слова (для, до, выполнить). Конкретно в курсовой работе цикл FOR используется для проведения циклического процесса вычисления сумм, являющихся элементами исходной матрицы коэффициентов: FOR i:=1 TO 25 DO Begin a1:=a1+X1[i]; {для x(i)} b1:=b1+Y1[i]; {для y(i)} c1:=c1+sqr(X1[i]); {для x(i)2} d1:=d1+X1[i]*Y1[i]; {для x(i)y(i)} e1:=e1+X1[i]*X1[i]*X1[i]; {для x(i)3} f1:=f1+X1[i]*X1[i]*X1[i]*X1[i]; {для x(i)4} g1:=g1+X1[i]*X1[i]*Y1[i]; {для x(i)2y(i)} end; Решение СЛАУ методом Гаусса Метод Гаусса – один из точных методов решения систем. Он состоит из прямого и обратного ходов. При прямом ходе матрица, составленная из коэффициентов уравнений системы, приводится к треугольному виду так, чтобы ниже ее главной диагонали оказались нули. Рассмотрим метод подробнее для системы:
Предположим, что
и вычтем из каждого i -го уравнения первое, помноженное на Обозначая легко убедится, что для всех уравнений, начиная со второго,
Преобразованная система уравнений запишется в следующем виде:
Аналогичным образом исключим х2 из последних (n-2) уравнений, получив новые коэффициенты. Эту операцию будем проводить пока система не примет вид:
Обратный ход. Он состоит в нахождении значений системы по формулам: из последнего уравнения вычисляем
Вывод В курсовой работе рассмотрено два варианта теоретической зависимости момента нагрузки M [кг·м] исполнительного органа угольного комбайна от толщины среза h [см] в MathCad и на языке программирования Turbo Pascal 7.0. Вычисления независимых расчётов сходятся, следовательно, – расчёты верны. В результате получились следующие формулы:
Давая качественную оценку коэффициентам детерминированности, опираясь на шкалу Чеддока, можно утверждать, что при линейной и квадратичной аппроксимациях наблюдается «весьма высокая» теснота связи между независимой переменной и предикатом (0,9–0,99), а это еще раз свидетельствует о правильности выбора функций для аппроксимации. При сравнении этих коэффициентов можно сказать, что уравнение линейной зависимости ( Библиографический список
Приложение 1
Приложение 2
Приложение 3 PROGRAM lineynaya; {подключение модуля, необходимого для процедур очистки экрана и задержки} USES CRT; {Задание массива} TYPE MAT=ARRAY [1..10,1..11] OF REAL; VEK=ARRAY [1..25] OF REAL; {Описание переменных} VAR i,j,n:INTEGER; A:MAT; X,B,X1,Y1:VEK; fr,fm:text; a1,b1,c1,d1:real; {Процедура Гаусса} PROCEDURE GAU(VAR A:MAT; VAR B,X:VEK; m:INTEGER); VAR k,i,j,t,L:INTEGER; D:REAL; fw:TEXT; BEGIN {Задание всех переменных} L:=m+1; FOR i:=1 TO m DO A[i,L]:=B[i]; {имя файла данных на диске} ASSIGN(fw,'gaus.txt'); REWRITE(fw); {запись данных в файл} WRITELN(fw,' CUCTEMA YPABHEHIY: '); {начальный вывод данных} FOR i:=1 TO m DO BEGIN FOR j:=1 TO m DO WRITE(fw,A[i,j]:14:6,' X[',j,'] '); WRITELN(fw,' = ', B[i]:14:6); END; {прямой ход решения СЛАУ по методу Гаусса} {формирование треугольной матрицы коэффициентов} FOR i:=1 TO m DO BEGIN D:=A[i,i]; t:=i; {ищем max в столбце} FOR j:=i TO m DO IF abs(A[j,i]) > abs(D) THEN BEGIN D:=A[j,i]; t:=j;END; {обмен строк} IF i<>t THEN BEGIN FOR j:=i TO L DO BEGIN D:=A[i,j]; A[i,j]:=A[t,j]; A[t,j]:=D;END; END; {формирование строки} FOR j:=L DOWNTO i DO A[i,j]:=A[i,j]/A[i,i]; {зануление столбцов и пересчет А} FOR k:=i+1 TO m DO FOR j:=L DOWNTO i DO A[k,j]:=A[k,j]-A[i,j]*A[k,i]; END; {обратный ход} X[m]:=A[m,L]; FOR i:=m-1 DOWNTO 1 DO BEGIN D:=0; FOR j:=m DOWNTO i+1 DO D:=D+A[i,j]*X[j]; X[i]:=A[i,L]-D; END; WRITELN(fw,' VEKTOR X: '); FOR i:=1 TO m DO WRITE(fw, X[i]:10:6); WRITELN(fw); CLOSE(fw) END; {вычисление сумм} BEGIN clrscr; {имя файла данных на диске} assign(fm,'kursovik.txt'); reset(fm); {чтение данных c файла} FOR i:=1 TO 25 DO read(fm,X1[i]); FOR i:=1 TO 25 DO read(fm,Y1[i]); FOR i:=1 TO 25 DO {формулы вычисления для сумм} begin a1:=a1+X1[i]; {для x(i)} b1:=b1+Y1[i]; {для y(i)} c1:=c1+sqr(X1[i]); {для x(i)2} d1:=d1+X1[i]*Y1[i]; {для x(i)y(i)} end; {имя файла данных на диске} assign(fr,'dan.txt');REWRITE(fr); {запись данных в файл} {Формирование матрицы А} write(fr,25,' '); writeln(fr,a1:4:4,' '); write(fr,a1:4:4,' '); writeln(fr,c1:4:4,' '); write(fr,b1:4:4,' '); writeln(fr,d1:4:4,' '); close(fr);
WRITELN(' РЕШЕНИЕ СЛАУ МЕТОДОМ ГАУССА. КОЛ-ВО УРАВН. НЕ БОЛЕЕ 10'); WRITELN; WRITE(' ВВОДИ ЧИСЛО УРАВНЕНИЙ: '); READLN(n); {имя файла данных на диске} assign(fr,'dan.txt'); reset(fr); {чтение данных с файла} FOR i:=1 TO n DO FOR j:=1 TO n DO READ(fr,A[i,j]); FOR i:=1 TO n DO READ(fr,B[i]); for i:=1 to n do begin for j:=1 to n do write(a[i,j]:14:6); writeln(B[i]:14:1); end; GAU(A,B,X,n); {вывод результатов} WRITELN('VEKTOR X:'); FOR i:=1 TO n DO WRITE(X[i]:12:6,' '); WRITELN; readln; END.
Результат работы программы CUCTEMA YPABHEHIY: 25.000000 X[1] 40.400000 X[2] = 34039.000000 40.400000 X[1] 86.316800 X[2] = 64484.880000 VEKTOR X: 633.272700 450.674072
Приложение 4 PROGRAM kvadratichnaya; {подключение модуля, необходимого для процедур очистки экрана и задержки} USES CRT; {Задание массива} TYPE MAT=ARRAY [1..10,1..11] OF REAL; VEK=ARRAY [1..25] OF REAL; {Описание переменных} VAR i,j,n:INTEGER; A:MAT; X,B,X1,Y1:VEK; fr,fm:text; a1,b1,c1,d1,e1,f1,g1:real; {Процедура Гаусса} PROCEDURE GAU(VAR A:MAT; VAR B,X:VEK; m:INTEGER); VAR k,i,j,t,L:INTEGER; D:REAL; fw:TEXT; BEGIN {Задание всех переменных} L:=m+1; FOR i:=1 TO m DO A[i,L]:=B[i]; {имя файла данных на диске} ASSIGN(fw,'gaus.txt'); REWRITE(fw); {запись данных в файл} WRITELN(fw,' CUCTEMA YPABHEHIY: '); {начальный вывод данных} FOR i:=1 TO m DO BEGIN FOR j:=1 TO m DO WRITE(fw,A[i,j]:14:6,' X[',j,'] '); WRITELN(fw,' = ', B[i]:14:6); END; {прямой ход решения СЛАУ по методу Гаусса} {формирование треугольной матрицы коэффициентов} FOR i:=1 TO m DO BEGIN D:=A[i,i]; t:=i; {ищем max в столбце} FOR j:=i TO m DO IF abs(A[j,i]) > abs(D) THEN BEGIN D:=A[j,i]; t:=j;END; {обмен строк} IF i<>t THEN BEGIN FOR j:=i TO L DO BEGIN D:=A[i,j]; A[i,j]:=A[t,j]; A[t,j]:=D;END; END; {формирование строки} FOR j:=L DOWNTO i DO A[i,j]:=A[i,j]/A[i,i]; {зануление столбцов и пересчет А} FOR k:=i+1 TO m DO FOR j:=L DOWNTO i DO A[k,j]:=A[k,j]-A[i,j]*A[k,i]; END; {обратный ход} X[m]:=A[m,L]; FOR i:=m-1 DOWNTO 1 DO BEGIN D:=0; FOR j:=m DOWNTO i+1 DO D:=D+A[i,j]*X[j]; X[i]:=A[i,L]-D; END; WRITELN(fw,' VEKTOR X: '); FOR i:=1 TO m DO WRITE(fw, X[i]:10:6); WRITELN(fw); CLOSE(fw) END; {вычисление сумм} BEGIN clrscr; {имя файла данных на диске} assign(fm,'kursovik.txt'); reset(fm); {чтение данных c файла} FOR i:=1 TO 25 DO read(fm,X1[i]); FOR i:=1 TO 25 DO read(fm,Y1[i]); FOR i:=1 TO 25 DO {формулы вычисления для сумм} begin a1:=a1+X1[i]; {для x(i)} b1:=b1+Y1[i]; {для y(i)} c1:=c1+sqr(X1[i]); {для x(i)2} d1:=d1+X1[i]*Y1[i]; {для x(i)y(i)} e1:=e1+X1[i]*X1[i]*X1[i]; {для x(i)3} f1:=f1+X1[i]*X1[i]*X1[i]*X1[i]; {для x(i)4} g1:=g1+X1[i]*X1[i]*Y1[i]; {для x(i)2y(i)} end; {имя файла данных на диске} assign(fr,'dan.txt');REWRITE(fr); {запись данных в файл} {Формирование матрицы А} write(fr,25,' ',a1:4:4,' '); writeln(fr,c1:4:4,' '); write(fr,a1:4:4,' ',c1:4:4,' '); writeln(fr,e1:4:4,' '); write(fr,c1:4:4,' ',e1:4:4,' '); writeln(fr,f1:4:4,' '); write(fr,b1:4:4,' ',d1:4:4,' '); writeln(fr,g1:4:4,' '); close(fr); WRITELN(' РЕШЕНИЕ СЛАУ МЕТОДОМ ГАУССА. КОЛ-ВО УРАВН. НЕ БОЛЕЕ 10'); WRITELN; WRITE(' ВВОДИ ЧИСЛО УРАВНЕНИЙ: '); READLN(n); {имя файла данных на диске} assign(fr,'dan.txt'); reset(fr); {чтение данных с файла} FOR i:=1 TO n DO FOR j:=1 TO n DO READ(fr,A[i,j]); FOR i:=1 TO n DO READ(fr,B[i]); for i:=1 to n do begin for j:=1 to n do write(a[i,j]:14:6); writeln(B[i]:14:1); end; GAU(A,B,X,n); {вывод результатов} WRITELN('VEKTOR X:'); FOR i:=1 TO n DO WRITE(X[i]:12:6,' '); WRITELN; readln; END.
Результат работы программы CUCTEMA YPABHEHIY: 25.000000 X[1] 40.400000 X[2] 86.316800 X[3] = 34039.000000 40.400000 X[1] 86.318600 X[2] 207.988022 X[3] = 64484.880000 86.318600 X[1] 207.988022 X[2] 535.163222 X[3] = 146684.350400 VEKTOR X: 412.112901 848.450296 -122.122397
Приложение 5
Приложение 6
КУРСОВАЯ РАБОТА
_________________________________________________________________________ (наименование учебной дисциплины согласно учебному плану)
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
_________________________________________________________________________ _________________________________________________________________________
Автор: студент гр. ГМ-10-1 ____________________ / Богославский Н. А. / (подпись) (Ф.И.О.)
ОЦЕНКА: _____________
Дата: ___________________
ПРОВЕРИЛ
Руководитель проекта ст. преп. ________________ / Кондрашев А. П. / (должность) (подпись) (Ф.И.О.)
Санкт-Петербург 2011 год
Кафедра Информатики и компьютерных технологий ____
КУРСОВАЯ РАБОТА
По дисциплине ___________________________________________________________ _________________________________________________________________________ (наименование учебной дисциплины согласно учебному плану) ЗАДАНИЕ
Студенту группы ГМ-10-1Богославский Н. А. (шифр группы) (Ф.И.О.)
__________________________________________________________________________________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Руководитель проекта ст. преп. ________________ / Кондрашев А. П. / (должность) (подпись) (Ф.И.О.) Дата выдачи задания: 15 сентября 2011г.
Аннотация Курсовая работа содержит расчеты, относящиеся к аппроксимации функциональной зависимости момента нагрузки М [кг·м] исполнительного органа угольного комбайна от толщины среза h [см] методом наименьших квадратов. В работе использовались средства MS Office: Microsoft Exel и Microsoft Word; расчеты проводились в Turbo Pascal, MathCAD. Курсовая работа содержит 35 страниц, 1 таблицу, 2 блок-схемы, 6 рисунка.
The Summary
Term paper contains calculations, related to approximations of functional dependence of the expense load torque M of the executive body of the coal shearer slice thickness h, by a least-squares method.. In it questions of construction of empirical formulas by a method of the least squares with elements of calculations in MathCAD and in programming language Turbo Pascal are considered. Approximating dependences are as a result received Term paper contains 35 pages, 1 table, 2 flow-charts, 6 pictures.
Оглавление Введение. 5 Решение в MS Excel 8 Аппроксимация эмпирических данных линейной зависимостью.. 8 Аппроксимация эмпирических данных квадратичной зависимостью.. 9 Элементы теории корреляции. 10 Решение задачи в Mathcad. 11 Аппроксимация линейной функцей. 11 Аппроксимация квадратичной функции. 13 Вычисление коэффициента детерминированности. 15 Решение задачи в среде Turbo Pascal 19 Описание программы.. 21 Решение СЛАУ методом Гаусса. 22 Вывод. 24 Библиографический список. 25 Приложение 1. 26 Приложение 2. 27 Приложение 3. 28 Приложение 4. 31 Приложение 5. 34
Введение Часто при анализе фактических результатов измерений или экспериментов возникает необходимость найти в явном виде функциональную зависимость между полученными фактическими величинами. Для нахождения аналитической взаимосвязи между двумя величинами M и h производят ряд наблюдений; в результате получается таблица измеренных значений. Поскольку табличные результаты получаются как итог каких-либо экспериментов, эти значения называются эмпирическими или опытными значениями. Таким образом, исходными данными являются два одномерных массива одинаковой длины, содержащие эмпирические данные. Если между величинами M и h существует некоторая функциональная зависимость, но ее аналитический вид неизвестен, то возникает практическая задача - найти эмпирическую формулу
где Вид функции и значения коэффициентов Нахождение аналитической зависимости между эмпирическими величинами называется аппроксимацией функции заданной таблично. При аппроксимации указывают класс функции, из которой выбирается теоретическая функция (например: линейная или кубическая и т.п.) и далее определяются наилучшие значения коэффициентов с помощью аппроксимации В курсовой работе рассматриваются методы по составлению вычислительных алгоритмов и программ в своей основной специальности “Горно-транспортные машины и оборудование”. Исходные данные заданы в виде двух одномерных табличных массивов. Таблица представляет собой итог экспериментально полученных величин, в результате работы исполнительного органа угольного комбайна, называемых эмпирическими. Горный (угольный) комбайн- комбинированная машина для одновременного выполнения операций по отделению от массива полезного ископаемого или породы и погрузки их на транспортные средства. Горный комбайн, предназначенный для добывания полезного ископаемого, называется очистным, а применяемый для проведения горных выработок- проходческим. Горный комбайн для проведения нарезных выработок по углю в целях подготовки очистного забоя называется нарезным. Наибольшее распространение горный комбайн получил в угольной промышленности. Горный комбайн (Рис. 1.) состоит из исполнительного органа (для отбойки, разрушения массива горных пород), погрузочного органа, роль которого в ряде случаев выполняет тот же исполнительный орган (для погрузки отбитой горной массы на транспорт), механизма передвижения, приводных двигателей, передаточных механизмов, органов управления и устройств для пылеподавления (оросительные системы) и пылеулавливания.
Рис. 1. Очистной комбайн узкозахватный типа с барабанным исполнительным органом для выемки пологих пластов. По конструкции и способу отделения горной массы различают несколько типов исполнительных органов горных комбайнов: · баровые, состоящие из одного или нескольких баров с режущими цепями, разрушающих массив системой зарубных щелей с последующим разрушением межщелевых целиков либо резанием с поверхности забоя · шнековые (с горизонтальной осью вращения), разрушающие массив резанием с поверхности забоя и перемещающие вдоль оси шнека отдельные куски горной массы на конвейер · буровые, разрушающие массив вырезанием концентрических тонких кольцевых щелей с последующим разрушением и погрузкой на конвейер межщелевых целиков · шарошечные, разрушающие массив системой шарошек Исполнительный орган горного комбайна в ряде случаев может быть комбинированным (например, буровой и барабанный, планетарный и шнековый). При проведении испытаний исполнительного органа угольного комбайна получена следующая зависимость момента нагрузки М от толщины среза h. Таблица 1 Зависимость момента нагрузки М [кг·м] исполнительного органа угольного комбайна от толщины среза h [см].
Построим график для выбора функций, с помощью которых будет производиться аппроксимация этой зависимости.
Рис. 2. График зависимости таблично заданных значений M и h. График зависимости, построенный по значениям табл.1 показывает, что для аппроксимации можно выбрать линейную и квадратичную функции. Решение в MS Excel Аппроксимация эмпирических данных линейной зависимостью
Согласно методу наименьших квадратов наилучшими коэффициентами а1, а2 считаются те, для которых сумма квадратов отклонения теоретической функции от заданных эмпирических значений будет минимальной. Находим коэффициенты а1(пересечение графика с осью ОУ) и а2(значение наклона), (т.к. любую прямую можно задать ее наклоном и У-пересечением) решая систему линейных уравнений, к которой нас приводит метод наименьших квадратов:
где: a1, a2 – коэффициенты аппроксимации, n = 25. Для этого составляем матрицу коэффициентов [A]и вектор Подробные вычисления по нахождению коэффициента корреляции представлены в приложении 5 и 6. Подставив, полученные коэффициенты в уравнение (1) получим: M=633,271+450,674h (1) и построим график с наложением эмпирических данных:
Рис.3.График имперических данных и теоретической линейной зависимости.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 532; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.182.179 (0.354 с.) |
 , (1)
, (1) — коэффициенты.
— коэффициенты.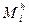 , вычисленные по эмпирической формуле при различных значениях
, вычисленные по эмпирической формуле при различных значениях  , возможно, мало отличались бы от опытных значений
, возможно, мало отличались бы от опытных значений 

 (3)
(3) — средние арифметические значения случайных величин h и M.
— средние арифметические значения случайных величин h и M. к 1, тем теснее линейная связь между h и M, и тем более справедлива аппроксимация таблично заданной функции линейной зависимостью.
к 1, тем теснее линейная связь между h и M, и тем более справедлива аппроксимация таблично заданной функции линейной зависимостью. (11)
(11) не равно нулю. Введем (n-i) множителей
не равно нулю. Введем (n-i) множителей (12)
(12) (13)
(13) . (14)
. (14) (15)
(15) (16)
(16) , далее находим
, далее находим  и из 1-го уравнения системы вычисляем:
и из 1-го уравнения системы вычисляем:
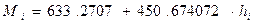 ,
, .
. ) удовлетворительно отображает экспериментальные данные. Но все же коэффициент детерминированности уравнения квадратичной зависимости ближе к единице (
) удовлетворительно отображает экспериментальные данные. Но все же коэффициент детерминированности уравнения квадратичной зависимости ближе к единице ( ) и достаточно хорошо отображает экспериментальные данные. На этом основании можно сделать вывод, что квадратичная зависимость наилучшим образом отображает взаимосвязь между M и h.
) и достаточно хорошо отображает экспериментальные данные. На этом основании можно сделать вывод, что квадратичная зависимость наилучшим образом отображает взаимосвязь между M и h.


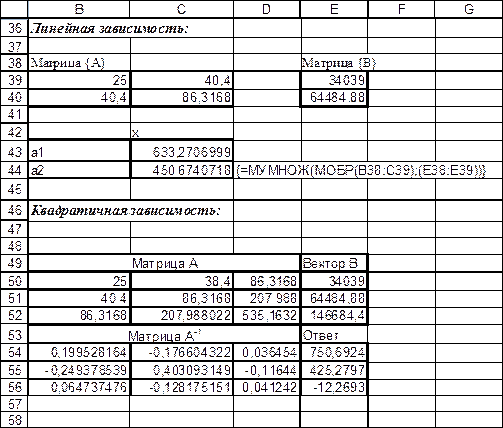


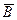 . Для нахождения коэффициентов пользуемся формулой (матричным методом):
. Для нахождения коэффициентов пользуемся формулой (матричным методом):  . Вектор
. Вектор  состоит из двух чисел, которые являются искомыми а1 и а2.
состоит из двух чисел, которые являются искомыми а1 и а2.



