
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
А. А. Башев, А. А. Кралин, Н. Г. ПанковаСтр 1 из 15Следующая ⇒
А.А. БАШЕВ, А.А. КРАЛИН, Н.Г. ПАНКОВА
ЭНЕРГЕТИЧЕСКАЯ ЭЛЕКТРОНИКА. СБОРНИК ЗАДАЧ
Часть 1
Рекомендовано Ученым советом Нижегородского государственного технического университета им. Р.Е. Алексеева в качестве учебного пособия для студентов очной, заочной и очно-заочной сокращенной форм обучения по направлениям подготовки 210100 «Электроника и наноэлектроника» 140400 «Электроэнергетика и электротехника»
Нижний Новгород 2014
УДК 621.3.011.71(075.8) ББК 31.264.5 я 73 Б331
Р е ц е н з е н т Заведующий кафедрой «Электротехника и электрооборудование объектов водного транспорта» Волжской государственной академии водного транспорта, доктор технических наук, профессор О.С. Хватов
Башев А.А., Кралин А.А., Панкова Н.Г. B331 Энергетическая электроника. Сборник задач. Часть 1: учеб. пособие / А.А. Башев [и др.]; Нижегород. гос. техн. ун-т им. Р.Е. Алексеева. – Нижний Новгород, 2014. – 127с.
ISBN
Рассматриваются темы упражнений для организации практических занятий по методам решения задач линейных цепей постоянного и переменного синусоидального тока, цепей трехфазного тока, электроники. По каждой теме приводятся краткие теоретические сведения и даются примеры решения типовых задач. Предназначено для студентов очной, заочной и очно-заочной сокращенной форм обучения.
Рис.58 Библиогр.: 6 назв.
УДК 621.3.013 ББК
ISNB © Нижегородский государственный технический университет им. Р.Е. Алексеева, 2014 © Башев А.А., Кралин А.А., Панкова Н.Г., 2014 ОГЛАВЛЕНИЕ 1. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА ………..……………………………………………………………....4 1.1. Основные определения и термины. Классификация и топологические понятия схем электрических цепей…………….4 1.2. Источники электрической энергии: источники ЭДС и источники тока ……………………………………………………..5 1.3. Законы Ома, Кирхгофа и закон сохранения энергии………………7 1.4. Эквивалентные преобразования пассивных участков электрической цепи …………………………………………………11 1.5. Методы расчета линейных электрических цепей ………………….15 2. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА ……………………………………….....29
2.1. Основные определения. Изображения синусоидальных функций времени векторами на комплексной плоскости …………………29 2.2. Активное сопротивление, индуктивность и конденсатор в цепи синусоидального тока….…………………………………............35 2.3. Комплексное сопротивление и проводимость. Законы Ома и Кирхгофа в комплексной форме. Векторные и потенциальные (топографические) диаграммы …………………………………………..40 2.4. Активная, реактивная и полная мощности. Баланс мощностей………………………………………………….....46 2.5. Методы расчета разветвленных цепей синусоидального тока, основанные на свойствах линейных цепей …………………..…....52 2.6. Резонансные режимы в цепи. Резонанс напряжения, резонанс токов. Частотные характеристики резонансных цепей.......56 2.7. Расчет цепей с индуктивно связанными элементами ……………...63 3. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ТРЕХФАЗНОГО ТОКА....……….......69 3.1. Основные определения. Трехфазная система ЭДС …..………….. 69 3.2. Схемы соединения трехфазных цепей …………….………...…….70 3.3. Расчет трехфазных цепей ……………………….……….................74 3.4. Активная, реактивная и полная мощности трехфазной системы...79 4. ПРАКТИЧЕСКАЯ ЧАСТЬ ………………………………..……………81 4.1.Цепи постоянного тока……………………………………………...81 4.2. Основы символического метода………………...…………………91 4.3. Расчет цепей символическим методом……………………………98 4.4. Трёхфазные цепи. Высшие гармоники в трёхфазных цепях…….117 СПИСОК ЛИТЕРАТУРЫ ……………………………………………..…125
Рис. 1.3 Рис. 1.4
К источникам тока обычно относят источники электромагнитной энергии, в которых ток не зависит от напряжения U, которое создается источником на зажимах приемника. Следовательно, источник тока представляет собой идеализированный источник питания, который создает ток I, не зависящий от сопротивления нагрузки, к которой он присоединен, а его ЭДС Е и внутреннее сопротивление R вн равны бесконечности. Вольт-амперная характеристика такого источника имеет вид, показанный на рис.1.5. Источниками тока являются, например, источники энергии, основанные на излучении заряженных частиц, выделяющихся при радиоактивном распаде вещества, так как при этом ток источника определяется скоростью распада.
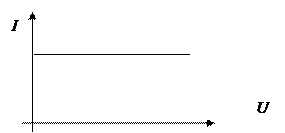
Рис.1.5
При расчете и анализе электрических цепей реальный источник электрической энергии с конечным значением R вн заменяют расчетным эквивалентом, в качестве которого может быть взят источник тока J к= E ит/ R ит с параллельно включенным R вн (рис.1.6). Стрелка в кружке показывает положительное направление тока источника тока. Отношение двух бесконечно больших величин E ит/ R вн равно конечной величине – току J к источника тока.

Рис.1.6
Ток в нагрузке (в сопротивлении R для схем рис.1.4 и 1.6) одинаков и равен I=E/(R вн +R). Каким из двух расчетных эквивалентов пользоваться, совершенно безразлично. Обратим внимание на следующее: 1) источник ЭДС и источник тока – идеализированные источники, физически осуществить которые, строго говоря, невозможно; 2) схема, представленная на рис. 1.4, эквивалентна схеме, приведенной на рис. 1.6, в отношении энергии, выделяющейся в сопротивлении нагрузки, и не эквивалентна ей в отношении энергии, выделяющейся во внутреннем сопротивлении источника питания R вн; 3) идеальный источник ЭДС без последовательно соединенногос ним сопротивления R вн нельзя заменить идеальным источником тока. Рис. 1.7 В соответствии с определением напряжение между точками а и b Uab= φ a- φ b. Следовательно, Uab=IR, т.е. напряжение на сопротивлении равно произведению тока, протекающего по сопротивлению, на значение этого сопротивления. В электротехнике разность потенциалов на концах сопротивления принято называть либо напряжением на сопротивлении, либо падением напряжения. Положительное направление падения напряжения на каком-либо участке (направление отсчета этого напряжения), указываемое на рисунках стрелкой, совпадает с положительным направлением отсчета тока, протекающего по данному сопротивлению. Рассмотрим вопрос о напряжении на участке цепи, содержащей кроме сопротивления R, ЭДС Е (рис. 1.8, а, б). Найдем разность потенциалов (напряжение) между точками а и с для этих участков. По определению Uaс= φ a- φ с. Выразим потенциал точки а через потенциал точки с. При перемещении от точки с к точке b встречно направлению ЭДС Е (см. рис. 1.8, а) потенциал точки b оказывается меньше, чем потенциал точки с, на значение ЭДС Е: φ b= φ c-E. При перемещении от точки с к точке b согласно направлению ЭДС Е (рис.1.8, б) потенциал точки b больше, чем потенциал точки с,на значение ЭДС: φ b= φ c+E. Так как ток течет от более высокого потенциала к более низкому, в обеих схемах потенциал точки а выше потенциала точки b на величину падения напряжения на сопротивлении R:φ а= φ b+IR.
а) б) Рис. 1.8
Таким образом, для рис. 1.8, а:
для рис. 1.8, б:
Положительное направление напряжения Uaс показывают стрелкой от а к с. Согласно определению, Uса= φ с- φ а, поэтому Uас=-Uса, т.е. изменение чередования индексов равносильно изменению знака этого напряжения. Следовательно, напряжение может быть как положительной величиной, так и отрицательной. Закон Ома для участка цепи, не содержащего ЭДС Е, устанавливает связь между током и напряжением на этом участке. Применительно к рис.1.7
Закон Ома для участка цепи, содержащего источник ЭДС Е, позволяет найти ток этого участка по известной разности потенциалов ( φ a- φ с) на концах этого участка цепи и имеющейся на участке ЭДС Е. Так, из уравнения (1.1) для схемы рис.1.8, а следует
Из уравнения (1.2) для схемы рис.1.8, б следует:
В общем случае
Все электрические цепи подчиняются первому и второму законам Кирхгофа. Первый закон Кирхгофа можно сформулировать двояко: 1) алгебраическая сумма токов, подтекающих к какому-либо узлу схемы, равна нулю; 2) сумма подтекающих клюбому узлу токов равна сумме утекающихот этого узла токов.
Рис. 1.9 Применительно к рис.1.9, если подтекающие токи к узлу считать положительными, а вытекающие - отрицательными, то согласно первой формулировке I 1 -I 2 -I 3 -I 4 = 0; согласно второй I 1 =I 2 +I 3 +I 4. Физически первый закон Кирхгофа означает, что движение электрических зарядов в цепи происходит так, что ни в одном из узлов они не скапливаются. В противном случае изменялись бы потенциалы узлов и токи в ветвях. Второй закон Кирхгофа также можно сформулироватьдвояко: 1) алгебраическая сумма падений напряженияв любом замкнутом контуре равна алгебраической сумме ЭДС, входящих в данный контур:
где m - число резистивных элементов; п – число ЭДС в контуре (в каждую из сумм соответствующие слагаемые входят со знаком плюс, если они совпадают с направлением обхода контура, и со знаком минус, если они не совпадают с ним); 2) алгебраическая сумма напряжений вдоль любого замкнутого контура
где т - число элементов контура. Второй закон Кирхгофа является следствием равенства нулю циркуляции вектора напряженности электрического поля вдоль любого замкнутого контура в безвихревом поле. Законы Кирхгофа справедливы длялинейных и нелинейных цепей при любом характере изменения во времени токов и напряжений. При протекании токов по сопротивлениям в них выделяется теплота. На основании закона сохранения энергии количество теплоты, выделяющееся в единицу времени в сопротивлениях цепи, должно равняться энергии, доставляемой за то же время источником питания. Если направление тока I, протекающего через источник ЭДС E, совпадает с направлением ЭДС, то источник ЭДС доставляет в цепь энергию в единицу времени, равную EI, и произведение ЕI входит в уравнение энергетического баланса с положительным знаком. Если же направление тока I встречно ЭДС Е, то источник ЭДС не поставляет энергию, а потребляет ее (например, заряжается аккумулятор), и произведение ЕI войдет в уравнение энергетического баланса с отрицательным знаком. Уравнение энергетического баланса при питании только от источников ЭДС имеет вид
В случае питания электрической цепи не только источниками ЭДС, но и источниками тока, при составлении уравнения энергетического баланса необходимо учесть и энергию, доставляемую источниками тока. Предположим, что к узлу а схемы подтекает ток J от источника тока, а от узла b этот ток утекает. Доставляемая источником тока мощность равна UаbJ. Общий вид уравнения энергетического баланса:
1.4. Эквивалентные преобразования пассивных участков электрической цепи При наличии в цепи только одного источника энергии в большинстве случаев цепь можно рассматривать как смешанное соединение источника и приемников энергии, т.е. нескольких резисторов, соединенных между собой параллельно, включенных последовательно с другими сопротивлениями (рис.1.10). Расчет смешанного соединения целесообразно начинать с определения эквивалентной проводимости параллельного соединения, а на основании этой проводимости легко найти обратную величину - эквивалентное сопротивление разветвления R. Для схемы, приведенной на рис. 1.10, а:
После замены разветвления эквивалентным сопротивлением (рис. 1.10, б) цепь можно рассчитывать как последовательное соединение; ток в неразветвленной части цепи:
а) б) Рис. 1.10
В ряде случаев расчет сложной схемы, состоящей из линейных сопротивлений, существенно упрощается, если в этой схеме заменить группу сопротивлений другой эквивалентной группой, в которой сопротивления соединены иначе, чем в замещаемой группе. Взаимная эквивалентность двух групп сопротивлений выразится в том, что после замены электрические условия во всей остальной схеме не изменятся. Рассмотрим преобразование звезды в треугольник и треугольника в звезду. Соединение трех сопротивлений, имеющих вид трехлучевой звезды, называют звездой (рис. 1.11), а соединение трех сопротивлений так, что они образуют собой стороны треугольника, - треугольником (рис.1.12). Обозначим токи, подтекающие к узлам 1, 2, 3, через I 1, I 2 и I 3. Выведем формулы преобразования. С этой целью выразим токи I 1, I 2 и I 3 в звезде и в треугольнике через разности потенциалов точек и соответствующие проводимости.
Рис. 1.11
Для звезды:
гдеφ о, φ 1, φ 2, φ 3 -потенциалы в точках 0, 1, 2, 3 соответственно. Подставим (1.10) в (1.9) и найдем φ 0:
Откуда
Подставим jо в выражение (1.10) для тока I 1:
С другой стороны, для треугольника в соответствии с обозначениями на рис. 1.12
Рис.1.12
Так как ток I 1 в схеме рис. 1.11 равен току I 1 в схеме рис. 1.12 при любых значениях потенциалов j1, j2 и j3, то коэффициент при j2 в правой части формулы (1.13) равен коэффициенту при j2 в правой части уравнения (1.12), а коэффициент при j3 в правой части формулы (1.13) равен коэффициенту при j3 в правой части уравнения (1.12). Следовательно,
Аналогично
Формулы (1.14), (1.15) дают возможность определить проводимости сторон треугольника через проводимости лучей звезды. Из уравнений (1.14)—(1.16) выразим сопротивления лучей звезды
С этой целью запишем дроби, обратные уравнениям (1.14)-(1.16):
где
Подставив формулы (1.17), (1.19) и (1.20) в выражение (1.18), получим
Следовательно,
Подставив m в выражение (1.19), найдем
Аналогично:
Структура формул (1.21)—(1.23) аналогична структуре формул (1.14) -(1.16).
Рис. 1.13 Решение. Произвольно выбираем положительные направления тока в ветвях. В схеме рис. 1.13 b =3; b ИТ=0; y =2. Следовательно, по первому закону Кирхгофа можно составить только одно уравнение y -1=1:
По второму закону Кирхгофа составим два уравнения. Положительные направления обхода контуров выбираем по часовой стрелке.
Для контура R 1 E 1 R 2 E 2
Знак плюс перед I 1 R 1 взят потому, что направление тока совпадает с направлением обхода контура, а знак минус перед I 2 R 2 потому, что направление I 2 встречно обходу контура. Для контура E 2 R 2 R 3 R 4:
Совместное решение трех уравнений дает I 1 = 14 A, I 2 = -15 A, I 3 = -1 A. В рассматриваемом примере отрицательными оказались токи I 2 и I 3, это следует понимать так, что в действительности токи I 2 и I 3 направлены в обратную сторону. Метод контурных токов При расчете методом контурных токов полагают, что в каждом независимом контуре схемы течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего через них определяют токи ветвей. Таким образом, метод контурных токов можно определить как метод расчета, в котором в качестве неизвестных принимают контурные токи. Число неизвестных в этом методе равно числу уравнений, составляемых для схемы по второму закону Кирхгофа. Преимуществом этого метода, по сравнению с методом на основе законов Кирхгофа, является меньшая вычислительная работа, так как в нем меньше уравнений. Вывод основных расчетных уравнений проведем применительно к схеме рис. 1.14, содержащей два независимых контура. Положим, что в левом контуре по часовой стрелке течет контурный ток I 11, а в правой (также по часовой) - контурный ток I 22. Для каждого из контуров составим уравнения по второму закону Кирхгофа. При этом учтем, что в смежной ветви (с сопротивлением Rs) течет сверху вниз ток I 11 - I 22. Направления обхода контуров примем также по часовой стрелке. Для первого контура
или
Для второго контура
или
Рис. 1.14
В уравнении (1.24) множитель при токе I 11, являющийся суммой сопротивлений первого контура, обозначим через R 11, множитель при токе I 22 (сопротивление смежной ветви, взятое со знаком минус), – через R 12. В уравнении (1.25) множитель при токе I 22, являющийся суммой сопротивлений второго контура, обозначим через R 22, множитель при токе I11 (сопротивление смежной ветви, взятое со знаком минус), – через R 21.
Перепишем эти уравнения следующим образом:
Здесь
где R 11 и R 22 - полное или собственное сопротивление первого и второго контуров соответственно; E 11 и Е 22 - контурные ЭДС первого и второго контуров, равные алгебраической сумме ЭДС этих контуров; R 12 = R 21 -сопротивление смежной ветви между первым и вторым контуром, взятое со знаком минус, так как контурные токи по ветви протекают встречно. Если в схеме больше контуров, например три, то система уравнений в общем виде выглядит следующим образом:
В результате решения системы уравнений (1.26) какой-либо один или несколько контурных токов могут оказаться отрицательными. В ветвях, не являющихся смежными между соседними контурами, найденный контурный ток является истинным током ветви. В смежных ветвях через контурные токи определяются токи ветвей. Если в электрической цепи имеется n независимых контуров, то число уравнений тоже равно n. Общее решение системы n -уравнений относительно тока Ikk таково:
где D - определитель системы.
Алгебраическое дополнение ∆ km, получено из определителя ∆ путем вычеркивания k -го столбца и m -й строки и умножения полученного определителя на (-1) k + m. Составлению уравнений по методу контурных токов для схем с источниками тока присущи некоторые особенности. В этом случае полагаем, что каждая ветвь с источником тока входит в контур, замыкающийся через ветви с источниками ЭДС и сопротивлениями, и что токи в этих контурах известны и равны токам соответствующих источников тока. Если для схемы рис. 1.15 принять, что контурный ток I 11 = J течет согласно направлению часовой стрелки по первой и второй ветвям, а контурный ток I 22 = I 3 замыкается также по часовой стрелке по второй и третьей ветвям, то, согласно методу контурных токов, получим только одно уравнение с неизвестным током I 22:
Отсюда

Рис. 1.15 Рис. 1.16
Токи в ветвях на основании закона Ома будут:
где φ1 и φ2- потенциалы узлов 1 и 2. После подстановки (1.28) в (1.27) и группировки членов получим:
или
В этих уравнениях g 11 = g 1 + g 4 + g 5 + g 6; g 22 = g 2 + g 3 + g 5 + g 6 - суммы проводимостей ветвей, присоединенных соответственно к узлам 1 и 2; g 12 = g 21 = =(g 5 + g 6) - сумма проводимостей ветвей, соединяющих эти узлы, взятая со знаком минус. Правая часть каждого из уравнений (1.30), равная алгебраической сумме произведений ЭДС источника на проводимость каждой из ветвей, присоединенных к рассматриваемому узлу, носит название узлового тока. Так как ток течет от более высокого потенциала к более низкому, в обеих схемах потенциал точки а выше потенциала точки b на величину падения напряжения на сопротивлении R:φ а= φ b+IR. Так как ток течет от более высокого потенциала к более низкому, в обеих схемах потенциал точки а выше потенциала точки b на величину падения напряжения на сопротивлении R:φ а= φ b+IR:
В общем случае gkk - сумма проводимостей ветвей, сходящихся в узле k, называется собственной узловой проводимостью этого узла; проводимость gkm - сумма проводимостей ветвей, непосредственно соединяющих узлы k и m, взятая со знаком минус, называется общей узловой проводимостью этих узлов. Если между какими-либо двумя узлами ветвь отсутствует, то соответствующая проводимость равна нулю. В формировании узлового тока k -узла Jkk участвуют те ветви, подходящие к этому узлу, которые содержат источники ЭДС и (или) тока. Если ЭДС Ep p -ветви направлена к k -узлу, то ее вклад в формирование Jkk составляет Еp g p, а если эта ЭДС направлена от k -узла, то ее вклад составляет - Еp g p , т.е. произведение Eg записывается со знаком плюс в том случае, когда ЭДС направлена к рассматриваемому узлу, и со знаком минус, когда ЭДС направлена от узла. Если к k -узлу подтекает ток от источника тока, то он должен быть введен в Jkk со знаком плюс, если этот ток от источника тока утекает, то он должен входить в Jkk со знаком минус. После решения системы (1.31) относительно потенциалов с помощью определителя получим:
где ∆ - главный определитель системы уравнений (1.31); ∆ km - алгебраическое дополнение, полученное из определителя ∆ путем вычеркивания k -гo столбца и m -строки и умножения полученного определителя на (-1) k+m. Рассмотрим применение уравнений (1.31) для частного случая схемы с двумя узлами и произвольным числом активных ветвей, когда требуется определить напряжение между этими узлами.
Рис. 1.17 Пусть между узлами 1 и 2 включено m ветвей (рис.1.17). Найдем напряжение U 12 = φ1 – φ2 = φ1 (узел 2 заземлен и φ2 = 0), записав уравнение (1.31) для первого узла:
где откуда
После определения напряжения U 12 находят ток в любой ветви по закону Ома. Рис. 1.19 В дальнейшем активные двухполюсники (рис. 1.20, а) будем обозначать прямоугольником с буквой А, а пассивные (рис. 1.20, б) - прямоугольниками с буквой П или без буквы П (просто прямоугольником).
а) б) Рис. 1.20 По отношению к выделенной ветви двухполюсник можно заменить эквивалентным генератором, ЭДС которого равна напряжению холостого хода на зажимах выделенной ветви, а внутреннее сопротивление равно входному сопротивлению двухполюсника. Пусть задана некоторая схема и требуется найти ток в одной ее ветви. Мысленно заключим всю схему, содержащую ЭДС и сопротивления, в прямоугольник, выделив из нее ветвь ab, в которой требуется найти ток I (рис.1.21, а). Ток I не изменится, если в ветвь ab включить две равные и противоположно направленные ЭДС: Е 1 и Е 2 (рис.1.21, б). На основании принципа наложения ток можно представить в виде суммы двух токов: I = I ' + I ''. Под током I будем понимать ток, вызываемый источником ЭДС Е 1 и всеми источниками ЭДС и тока активного двухполюсника, заключенными в прямоугольник. Ток I вызывается только одним источником ЭДС Е 2. В соответствии с этим для нахождения токов I ' и I '' используем схемы рис.1.21, в, г. В прямоугольнике П (рис.1.21, г) отсутствуют все источники, но оставлены их внутренние сопротивления.
а) б)
в) г) Рис. 1.21 Электродвижущая сила Е 1, направлена встречно напряжению Uab. По закону Ома для участка цепи, содержащего ЭДС,
Выберем Е 1 так, чтобы ток I ' был равен нулю. Отсутствие тока в ветви ab эквивалентно ее размыканию (холостому ходу). Напряжение на зажимах ab при холостом ходе ветви обозначим Uabx. Следовательно, если выбрать Е 1 = Uabx, то в соответствии с (1.36) I '= 0. Так как I = I '+ I '', а I '= 0, то I = I ''. Но ток I '' в соответствии со схемой (рис. 1.21, г) определяется как
где R вx - входное сопротивление двухполюсника по отношению к зажимам ab; R - сопротивление ветви аb. Уравнению (1.37) отвечает эквивалентная схема рис.1.22, а, где вместо двухполюсника изображены источник ЭДС UаЬx = Е 2 и сопротивление R вx.
а) б) Рис. 1.22 Совокупность источника ЭДС Е 2 = Uabx и сопротивления R вx можно рассматривать как некоторый эквивалентный генератор (R вх является его внутренним сопротивлением, а Uabx - его ЭДС). Таким образом, по отношению к выделенной ветви (ветви ab на рис.1.21, а) всю остальную часть схемы можно заменить эквивалентным генератором с перечисленными значениями параметров. Метод расчета тока в выделенной ветви, основанный на замене активного двухполюсника эквивалентным генератором, принято называть методом эквивалентного генератора (активного двухполюсника), а также методом холостого хода и короткого замыкания. Рекомендуется такая последовательность расчета тока этим а) найти напряжение на зажимах разомкнутой ветви ab; б) определить входное сопротивление R вx всей схемы по отношению к зажимам ab при закороченных источниках ЭДС и разомкнутых ветвях с источниками тока; в) подсчитать ток по формуле
Если сопротивление ветви a b равно нулю (R = 0), то для нее имеет место режим короткого замыкания, а протекающий по ней ток есть ток короткого замыкания (Ik). Из формулы (1.38) при R = 0
или
Из формулы (1.40) следует метод опытного определения входного сопротивления активного двухполюсника. Для этого необходимо измерить напряжение холостого хода на зажимах разомкнутой ветви U вх и ток короткого замыкания I к ветви. Заменив источник ЭДС источником тока, получим схему эквивалентного генератора, предоставленную на рис. 1.22, б.
Рис. 2.1 Представим синусоидальные токи i 1 и i 2 в виде двух радиус - векторов, длина которых равна в соответствующем масштабе I 1 m и I 2 m . Эти векторы расположены в начальный момент времени под углами φ1 и φ2 относительно горизонтальной оси. Сложим геометрически отрезки I 1 m и I 2 m . Получим отрезок, длина которого равна амплитудному значению результирующего тока I 3 m . Отрезок расположен под углом φ3 относительно горизонтальной оси. Все три отрезка вращаются вокруг оси 0 с постоянной угловой скоростью ω. Проекции отрезков на вертикальную ось изменяются по синусоидальному закону. Будучи остановленными, данные отрезки образуют векторную диаграмму (рис. 2.2). Векторная диаграмма - это совокупность векторов, изображающих синусоидальные напряжения, токи и ЭДС одинаковой частоты. Необходимо отметить, что напряжение, ток и ЭДС - это скалярные, а не векторные величины. Мы представляем их на векторной диаграмме в виде не пространственных, а временных радиус - векторов, вращающихся с одинаковой угловой скоростью. Положительным считается направление вращения векторов против часовой стрелки. Изображать на векторной диаграмме два вектора, вращающихся с различной угловой скоростью, нельзя.
Рис. 2.2 При расчетах цепей синусоидального тока используют символический метод расчета или метод комплексных амплитуд, в котором синусоидально изменяющиеся функции изображаются векторами на комплексной плоскости. Из курса математики известно, что комплексное число может быть записано в показательной или алгебраической форме:
где с - модуль комплексного числа; φ- аргумент; a=Re ( С помощью формулы Эйлера можно перейти от показательной формы записи комплексного числа к алгебраической:
От алгебраической формы записи переходят к показательной форме с помощью формул:
Комплексное число может быть представлено в виде радиус - вектора на комплексной плоскости с длиной, равной модулю c, расположенного в начальный момент времени под углом φ относительно вещественной оси (рис.2.3).
Рис. 2.3 Умножим комплексное число на множитель ej β. Радиус - вектор на комплексной плоскости повернется на угол βпротив часовой стрелки. Множитель ej β называется поворотным:
Отметим очевидные соотношения при следующих значениях угла β:
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 515; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.31.159 (0.274 с.) |


 (1.1)
(1.1) (1.2)
(1.2) или
или  . (1.3)
. (1.3) .
. .
. . (1.4)
. (1.4)
 , (1.5)
, (1.5) , (1.6)
, (1.6) . (1.7)
. (1.7) . (1.8)
. (1.8)





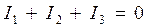 , (1.9)
, (1.9) ;
; 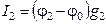 ;
;  , (1.10)
, (1.10) .
. . (1.11)
. (1.11) . (1.12)
. (1.12) . (1.13)
. (1.13)
 (1.14)
(1.14) . (1.15)
. (1.15)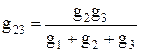 . (1.16)
. (1.16) ;
;  ;
;  через сопротивления сторон треугольника:
через сопротивления сторон треугольника: ;
;  ;
;  .
. ; (1.17)
; (1.17) , (1.18)
, (1.18) ; (1.19)
; (1.19) . (1.20)
. (1.20) .
. .
. . (1.21)
. (1.21) ; (1.22)
; (1.22) . (1.23)
. (1.23) .
. .
. .
.
 . (1.24)
. (1.24)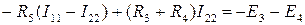
 . (1.25)
. (1.25)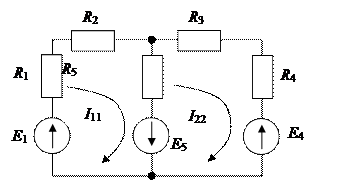
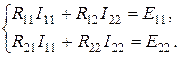

 (1.26)
(1.26) , (1.27)
, (1.27) .
. .
. и ток второй ветви I 2= I 11- I 22= J - I 22.
и ток второй ветви I 2= I 11- I 22= J - I 22.
 (1.28)
(1.28) (1.29)
(1.29) (1.30)
(1.30) (1.31)
(1.31)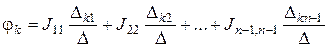 , (1.32)
, (1.32)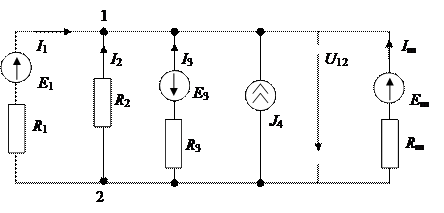
 ,
,
 ,
, . (1.33)
. (1.33)




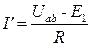 . (1.36)
. (1.36)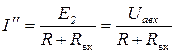 , (1.37)
, (1.37)
 . (1.38)
. (1.38) (1.39)
(1.39) . (1.40)
. (1.40)
 ,
, ) – действительная часть; b=Im (
) – действительная часть; b=Im ( .
. ;
; ;
; 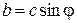 .
. ; φ=arctg
; φ=arctg  .
.
 .
.



