
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристики нормального розподілу
- Математичне очікування. Середнє значення. Математичним очікуванням М(х) дискретної випадкової величини х називається сума добутків всіх можливих значень випадкової величини помножена на імовірність цих значень рі і записується формулою: М(х)=å хі ×рі. (8.3) Для неперервних випадкових величин просте сумування неможливе. Тому математичне очікування записується наступним чином: М(х)=ò-¥ х × j(х) d x, (8.4) де x – випадкова величина; j(х) – ординати для кожного значення х; d x – елементарні відрізки осі абсцис. Якщо розглядати нормальний розподіл випадкових величин (Малюнок 8.4), то математичне очікування буде відповідати істинному значенню випадкової величини х. На практиці для визначення істинного значення випадкової величини приймають середнє арифметичне значення ряду випадкових величин, що обчислюється за формулою:
де хі –поточне значення випадкової величини; N – число випадкових величин. Доказано, що середнє арифметичне значення являється наближеним до істинного значення, тобто його математичним очікуванням для даних умов вимірювання. На малюнку 8.4 середнє значення, а значить і істинне значення випадкової величини дорівнює нулю. - Дисперсія Криві нормального розподілу можуть мати різний вигляд. На малюнку 8.5 наведено приклади кривих нормального розподілу випадкових величин з різним математичним очікуванням і розкидом результатів вимірювання.
Мал. 8.5. Криві нормального розподілу Крива 1, позначена суцільною лінією, – вся площина зосереджена біля ординати, а значить більшість результатів мало відрізняється від математичного очікування, що дорівнює нулю; Крива 2, позначена крапками, – площина розосереджена, має великий розкид результатів. Тут математичне очікування теж дорівнює нулю. Крива 3, позначена штриховою лінією, – вся площина зосереджена біля математичного очікування, що дорівнює п’яти. Розкид випадкових величин такий же, як у кривій 1. Мірою розсіювання (розкиду) випадкових величин служить дисперсія D(x), що позначається s2. Дисперсія дискретних випадкових величин визначається як:
Дисперсія неперервних випадкових величин записується формулою
- Середнє квадратичне відхилення
Для характеристики розсіювання частіше всього користуються середнім квадратичним відхиленням, що визначається як корінь квадратний від дисперсії.
Теоретично доказано, що для отримання s за результатами експериментальних даних середнє квадратичне відхилення потрібно визначати в іншому нормуванні за формулою:
Чим більше вимірювань N, тим точніше визначено s. - Коваріація і кореляція Функції, що встановлюють зв'язок між парами двох випадкових векторів, називаються коваріацією і кореляцією. (або по іншому коефіцієнтом кореляції). Вони розрізняються нормуванням, як це витікає з визначення.Для двох випадкових величин x та y коваріація визначається за формулою
де Mx та My – математичні очікування випадкових величин x і y. Для незалежних випадкових величин коваріація дорівнює нулю. К оефіцієнт кореляції є коваріація нормована на корінь квадратний з добутків дисперсій Dx та Dy випадкових величин:
Кореляція визначається за формулою:
- де s1, s2 - середні квадратичні відхилення випадкових величин. Л Логічні оператори: призначення, способи створення і застосування, приклади. Логічні оператори Результатом дії логічних, або булевих, операторів являються тільки числа 0 (якщо логічний вираз відповідає істині) або 1 (якщо логічний вираз відповідає хибному результату). Логічні оператори вставляються з панелі Boolean (Булеві оператори). На ній розміщені оператори порівняння (відношення) та булеві оператори (Мал. 2.1). . Мал. 2.1 Вставка логічних операторів з панеліBoolean Перерахуємо логічні оператори: Застосування операторів порівняння та булевих операторів приведено в прикладах 2.13 та 2.14.
Приклад 2.13 Оператори порівняння
Логічні оператори надзвичайно важливі для записів алгебраїчних рівнянь і нерівностей у прийнятній для Mathcad формі.
М
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 433; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.252.140 (0.009 с.) |
 , (8.5)
, (8.5) - середнє значення;
- середнє значення;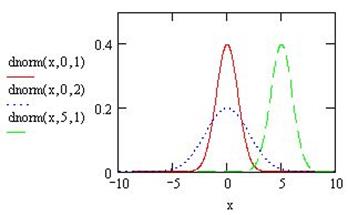
 (8.6)
(8.6) (8.7)
(8.7) (8.8)
(8.8) 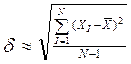
 , (8.10)
, (8.10) (8.11)
(8.11) , (8.12)
, (8.12)
 );
); );
); ), (Ctrl + 0);
), (Ctrl + 0);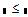 ), (Ctrl + 9);
), (Ctrl + 9); ), (Ctrl + =);
), (Ctrl + =); ), (Ctrl + 3);
), (Ctrl + 3); ), (Ctrl +Shift + 7);
), (Ctrl +Shift + 7); ), (Ctrl +Shift + 6);
), (Ctrl +Shift + 6); ), (Ctrl +Shift + 5);
), (Ctrl +Shift + 5); ), (Ctrl +Shift + 1).
), (Ctrl +Shift + 1).




