
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип детектирования АМ-сигналов
На вход детектора поступает АМ сигнал, который в простейшем случае имеет вид Эта операция осуществляется цепью, состоящей из трех основных элементов: нелинейного элемента, фильтра и нагрузки.
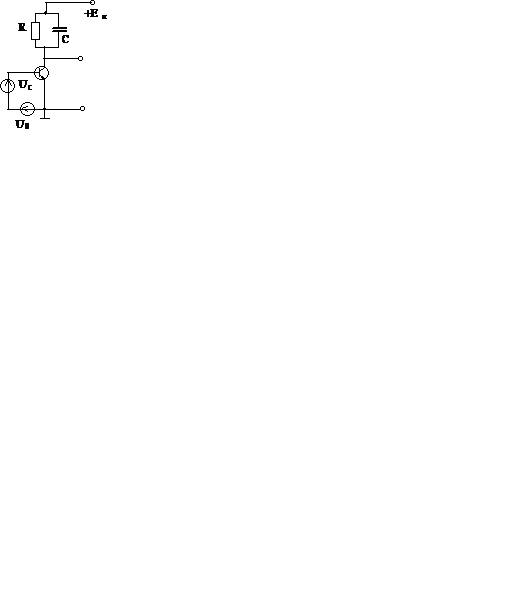
Нелинейный элемент искажает форму колебаний и изменяет частотный спектр их таким образом, что в составе преобразованного колебания появляется компонента с частотой, соответствующей огибающей АМ колебаний. Этот компонент тока поступает в нагрузку (активное сопротивление) и создает на ней пропорциональное напряжение. Остальные (высокочастотные) компоненты тока отводятся от нагрузки через фильтр. Рассмотренная блок-схема является общей для амплитудных детекторов всех типов. Хорошая работа любого детектора возможна лишь при правильном выборе режима нелинейного элемента и параметров нагрузки и фильтра. Сущность процесса детектирования наиболее просто проанализировать на примере коллекторного детектора.
Предположим, что амплитуда входного сигнала велика настолько, что, не боясь больших погрешностей в расчете, можно представить рабочий участок вольтамперной характеристики нелинейного элемента в виде кусочно линейного.
Воздействие АМ колебаний вызовет появление в коллекторной цепи импульсов тока, величина которых будет изменяться по закону огибающей, а угол отсечки для всех импульсов будет равен
22) Дискретные сигналы. Дискретное преобразование Фурье Сигнал называется дискретным, если он может принимать лишь конечное число значений. Дискретные сигналы начали использовать с импульсной модуляцией. Этот вид модуляции отличается тем, что в качестве несущего колебания вместо гармонического сигнала служит периодическая последовательность коротких импульсов. U
t На выходе модулятора возникает последовательность импульсов, каждый из которых имеет площадь, соответствующую отсчетному значению аналогового сигнала. Сигнал хМИП(t) на выходе из модулированной импульсной последовательности. спектр дискретизирующей последовательности состоит из бесконечной совокупности дельта импульсов.
Т.е. спектр сигнала, полученного в результате идеальной дискретизации бесконечно короткими стробирующими импульсами, представляет собой сумму бесконечного числа “копий” спектра исходного аналогового сигнала.
N=T/ -интервал дискретизации
Формула (6) определяет последовательность коэффициентов, образующих дискретное преобразование Фурье (ДПФ).
Свойства ДПФ. 1. ДПФ есть линейное преобразование. 2. Коэффициент С0 (постоянная составляющая) является средним значением всех отсчетов
3. Если отсчетные значения xk - вещественные числа, тогда коэффициенты ДПФ, номера которых располагаются симметрично относительно N/2, образуют сопряженные пары. Предположим, что коэффициенты Сn, образующие ДПФ, заданы для того, чтобы вычислить отсчетные значения, используют обратное дискретное преобразование Фурье:
23) Дискретные сигналы. Теория z - преобразований. Сигнал называется дискретным, если он может принимать лишь конечное число значений. Дискретные сигналы начали использовать с импульсной модуляцией. Этот вид модуляции отличается тем, что в качестве несущего колебания вместо гармонического сигнала служит периодическая последовательность коротких импульсов. U
t
На выходе модулятора возникает последовательность импульсов, каждый из которых имеет площадь, соответствующую отсчетному значению аналогового сигнала. Сигнал хМИП(t) на выходе из модулированной импульсной последовательности. спектр дискретизирующей последовательности состоит из бесконечной совокупности дельта импульсов.
Т.е. спектр сигнала, полученного в результате идеальной дискретизации бесконечно короткими стробирующими импульсами, представляет собой сумму бесконечного числа “копий” спектра исходного аналогового сигнала. Теория z - преобразований. Пусть {xk} = {x0,x1,x2,...} - числовая последовательность, содержащая отсчетные значения некоторого сигнала. Поставим ей в однозначное соответствие сумму ряда по отрицательным степеням комплексной переменной z:
Эта сумма называется z - преобразованием последовательности {xk} использование z - преобразования позволяет изучать дискретные сигналы методами математического анализа непрерывных функций.
На основании формулы (8) можно непосредственно найти z - преобразование дискретных сигналов с конечным числом отсчетов. Так, простейшему дискретному сигналу с единственным отсчетом {xk} = {1,0,0,...} соответствует X(z) = 1. Если же, например, {xk} = {1,1,1,0,0,0,...}, то
Полагая, что отсчеты {xk} есть значения непрерывной функции x(t) в точках t = kD, любому сигналу x(t) можно сопоставить его z - преобразование при выбранном шаге дискретизации:
Например, если x(t) = exp(at), то соответствующее z - преобразование:
Если в формуле (9) положить z = exp(jwD), то выражение
будет преобразованием Фурье.
|
||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 967; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.96.159 (0.007 с.) |
 . Задача детектора состоит в том, чтобы преобразовать АМ колебание в напряжение, изменяющееся по закону их огибающей, т.е. в данном случае в напряжение
. Задача детектора состоит в том, чтобы преобразовать АМ колебание в напряжение, изменяющееся по закону их огибающей, т.е. в данном случае в напряжение 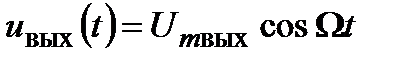


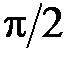 .
.
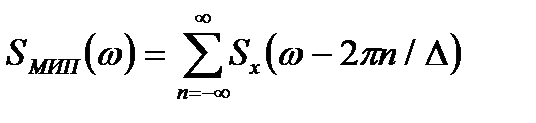
 (6)
(6)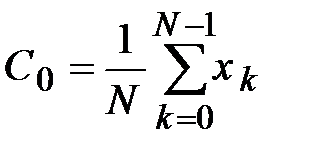
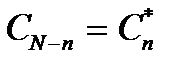 .
.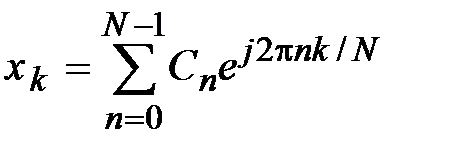
 (8)
(8)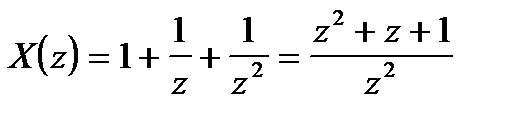 .
.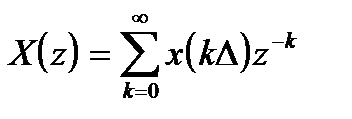 (9)
(9)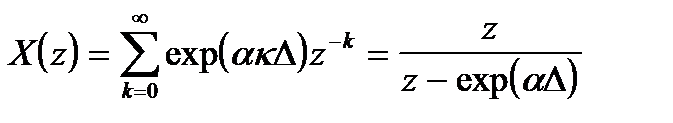
 (10)
(10)


