Какие основные алгоритмы картопостроения вы знаете.

Алгоритм	Набор из большого количества точек	Набор из нескольких точек	Возможность экстраполяции	Корректная поддержка разломов	Данные, доступные в качестве основных исходных (Main input)
2D&3D lines, Contours	Points	Well points, Well points&trend	Original surface	Isochore data
Mask method	да	да	да	да	да	да	да	да	да
Cos expansion		да	да			да	да		да
Moving average		да	да			да	да		да
Parabolic		да	да			да	да		да
Polynominal least squares		да	да			да	да		да
Radial basis		да	да			да	да		да
Seabed	да		да	да	да	да		да	да
Snapping	да				да	да		да	да
Triangulate	да	да		да	да	да			да
Closest point			да						да
Smart			да						да
Constant			да						да
Fractal			да						да

 

Возможность экстраполяции необходима, когда не задается граница построений. В этом случае поостренная поверхность будет покрывать всю область проекта.

 

Mask Method – является универсальным, может быть использован в случае небольшого числа точек и тогда, когда имеется большое число точек (>100). Метод позволяет минимизировать кривизну получаемой поверхности. Дает хорошие результаты при неравномерном распределении исходных данных. Хорошо подходит как при работе с точками и линиями, так и при моделировании разломов.

Работает алгоритм в два этапа и включает в себя сначала локальную (local), а затем глобальную интерполяцию (global).

При локальной интерполяции (Local interpolation) около каждого узла сетки строится окружность определенного радиуса, и собираются все точки с исходными данными, которые видны из узла сетки и попадают в эту окружность (термин “видны” означает, что между узлом сетки и точками нет линий разломов, разделяющих их). Те узлы сетки, из которых окружность захватила хотя бы одну точку с исходными данными, определяются как “узлы данных”. Им присваивается z -значение путем интерполяции z-значениями ближайших к ним точек.

Глобальная интерполяция (Global interpolation) используется для расчета оставшихся неопределенных узлов сетки. Это делается на основании интерполяции значений “узлов данных”, полученных в результате локальной интерполяции.

В панели настроек Mask method можно задать радиус окружности для сбора точек вокруг узлов сетки на этапе локальной интерполяции. Возможно использование только алгоритма локальной интерполяции. Существует выбор методов и для локальной, и для глобальной интерполяции.

 

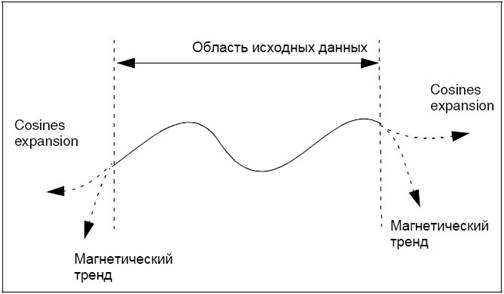
Cos Expansion – алгоритм картопостроения, основанный на работе с точками. При этом работает как с большим количеством точек, так и с наборами из нескольких сотен. Однако, при большом количестве точек, работа алгоритма может занимать большое количество времени. Алгоритм позволяет получать хорошие результаты даже при использовании 2 или 3 точек. Использование этого алгоритма позволяет избежать «краевых эффектов», поэтому он может использоваться при картировании больших неопределенных областей.

В настройках можно задать вес тренда в пределах от 1 до 10 и вес тренда в географических градусах.

Moving average - используется для большого числа точек. Работа метода заключается в получении средневзвешенного значения исходных точек, основываясь на формуле:

Z= , где m ≥1 и D_i ≤ D_max

z_i – это Z -значение для выбранной точки с номером i,

N – количество исходных точек

D_i – расстояние от точки с номером i до (х, y)-позиции узла сетки, для которого рассчитывается Z -значение

m – значение степени, по умолчанию равное 2.

В настройках алгоритма задаются минимальный и максимальный радиусы поиска исходных точек, весовой коэффициент для исходных точек, минимальное число точек в радиусе поиска для присвоения Z -значения узлу сетки и значение степени m.

 

Parabolic – для этого алгоритма необходимо иметь минимум 4 точки. Алгоритм дает корректный учет всех исходных точек. При этом получаемая поверхность будет иметь свои экстремальные значения (минимум и максимум), там, где они располагаются наилучшим образом. Это означает, что экстремумы могут располагаться далеко от исходных данных, если в их поведении имеется отчетливая зависимость. Изолинии контуров на поверхности имеют логическое расположение и расстояние друг между другом, на границах поверхности не создаются флуктуации. Но алгоритм не может использовать большое количество точек. К тому же он дает «краевые эффекты».

В работе алгоритма для задания параболоида в пространстве используется следующая математическая формула:

z = a(x² + y²) + bx + cy + d, где a, b, c и d удовлетворяют следующим критериям:

Min

Форма параболоида определяется таким образом, что квадрат расстояния от исходных точек до параболоида минимален. Каждой из исходных точек присваивается весовой коэффициент таким образом, чтобы ближайшие к узлу сетки точки имели бы наибольший приоритет при вычислении z-значения узла сетки. Вес точки увеличивается пропорционально квадрату ее расстояния от узла сетки.

 

Polynomial – алгоритм, который позволяет аппроксимировать исходные точки поверхностью методом наименьших квадратов, используя полиномы различных степеней. В панели Settings опция degree позволяет выбрать полином той или иной степени:

Degree

0 Þ L (x,y) = a

1 Þ L (x,y) = a + bx + cy

2 Þ L (x,y) = a + bx + cy + dxy + ex² + fy²

Во всех случаях используется метод наименьших квадратов.

Radial Basis – это хорошо себя зарекомендовавший способ интерполяции разрозненных данных. Алгоритм рекомендуется использовать только для среднего числа точек (>=100). Метод основывается на линейной комбинации радиальных функций с центрами в каждой из исходных точек. Интерполяционная функция имеет вид:

f (x) =

Коэффициент c_i рассчитывается путем решения систем линейных уравнений, число которых равняется числу исходных точек. От выбора радиальной функции в панели Settings зависит метод интерполяции:

Linear - j (r) = r / diag

Cubic - j (r) = (r / diag)³

Thinplate spline - j (r) = (r / diag)² log (r / diag)

Gaussian - j(r) = e^{-(r/diag )}

Multi quadric - j(r) =

Inv multi quadric - j(r) = 1/

где diag – диагональ окна данных, а константа с рассчитывается по формуле

с ² = 0.815 p /4 n

 

Seabed – алгоритм хорош для данных высокой плотности, например, результатов акустического зондирования морского дна. Однако, он может использоваться и для других типов данных (2D, 3D сейсмика). Основывается алгоритм на том, что узлам сетки присваиваются z -значения, исходя из следующих предположений:

 

1. Создание “локальных наборов точек” из ближайших к узлам сетки исходных данных

2. Интерполяция “локальных наборов точек” с использованием заданных интерполяционных алгоритмов

 

Snapping – это алгоритм аналогичный Moving average, но для большого числа точек. Он является самым быстрым для создания поверхностей из набора точек. Но в этом алгоритме нельзя использовать информацию о разломах. Работает он в два этапа:

1. Для каждой исходной точки выполняется действие, при котором точка добавляется в ближайшие n узлов сетки. Число таких узлов задается в панели Settings и может быть в диапазоне 1-16.

2. Последовательно для всей сетки осуществляется весовое осреднение всех точек, которые были добавлены к узлам сетки.

 

Triangulate – алгоритм осуществляет различные виды триангуляций разрозненных данных с возможностью учета информации о разломах, границах и отверстиях. Результирующая поверхность не будет представлять собой регулярную сетку, а будет состоять из набора треугольников, покрывающих область исходных данных. Триангуляция внутри заданных отверстий и вне заданных границ не осуществляется.

В настройках Settings можно выбрать два метода триангуляции:

Delaunay – нормальная триангуляция. Установлена по умолчанию

Approximative – триангуляция с учетом z -значений в точках. При этом можно менять величину погрешности Tolerance между z -значением точки и результатом Approximative триангуляции.

Для обоих методов триангуляции также существует опция Use boundary intriangulation, которая позволяет учитывать границы проекта при триангуляции. Когда опция выключена, поверхность будет строиться только внутри границы, а если выключена, то границы будут встроены в поверхность.

12. Назовите основные принципы создания параметра песчанистости.