
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ряды динамики. Виды рядов динамики.
Ряды динамики – ряд последовательно расположенных статистических показателей (в хронологическом порядке) изучения которых показывает определенную тенденцию различия изучаемого явления. В каждом ряду динамики имеется 2 основных элемента: Время (t) Уровень ряда (y) Виды рядов динамики: 1. Моментные – на определенную дату (моментальных рядов суммировать нельзя – сумма не имеет смысла, однако разные уровни имеют смысл, увеличение или уменьшение уровня ряда между рядами учета.) 2. Интервальные – за определенный период (приводятся данные характеризующие величину за определенные периоды (сутки, месяц итд). Уровни можно суммировать получая новые численные значения, объема явлений.) Такие ряды могут быть полными и неполными. Полный ряд – ряд динамики, в котором одинаковые моменты времени или периоды времени строго следует один за другим. Неполный ряд – это ряд, в котором уровни зафиксированы в равностоящие моменты или периоды времени. Приведение рядов динамики в сопоставимый вид. Ряды динамики изучающие изменения показателя могут охватывать значительный период времени на протяжении кот. Могут происходить события нарушающие сопоставимость отдельных уровней ряда динамики. Для того, чтобы анализ ряда был объективен, необходимо учитывать события приводящие к несопоставимости уровней ряда и использовать приемы обработки рядов для приведения их в сопоставимый вид. Для приведения к сопоставимому виду определяем коэффициент перерасчета. Кп = Показатели ряда динамики. 1. Абсолютные: (приросты) Цепные Базисные 2. Относительные Цепные (Тр; Тпр) Базисные (Тр; Тпр) Если приводится сравнение каждого уровня к предыдущему уровню – цепные. Если каждый уровень сравнивается с каждым уровнем или уровнем принимаемым за базу уровня – базисные. При расчете показателей приняты следующие обозначения Уi – уровень любого периода кроме 1-ого называется уровнем текущего периода. Уi-1 – уровень предшествующего периода к текущему Ук – уровень периода принятого за базу сравнения Средние показатели динамики. 1. Средний уровень ряда – это показатель, который обобщает итоги развития явления за единственный интервал или момент. 1.1 Для интервальных рядов
n – количество периодов. y = 1.2 Для моментного ряда с равностоящими датами y = 1.3 Для моментного с неравностоящими датами: y = t – продолжительность интервала времени между соседними уровнями. 2. Средний абсолютный прирост – представляет собой обобщенную характеристику индив. абсолютных приростов ряда динамики.
3. Средний темп роста – это обобщенная характеристика индивид. темпов роста динамики. Т 4. Средний темп прироста. Тпр = Тр *100 Понятие индекс. Условные обозначения, используемые в теории индексного метода. Индексы – это относительные показатели сравнения двух состоящих простого и сложного явления. Состоит из соизмеримых и несоизмеримых элементов во времени или пространстве. Основные задачи индексного метода. 1. Оценка динамики обобщающих показателей характеризующие сложные, непосредственно несоизмеримые в совокупности. 2. Анализ влияния отдельных факторов на изменения результативных обобщающих показателей. 3. Анализ влияния структурных сдвигов на изменения средних показателей однородной совокупности. 4. Оценка территориальных, в том числе международных сравнений.
Индивидуальные индексы – характеризуют изменение отдельных единиц в статистической совокупности. Общие индексы – выражают сводные результаты совместимого изменения всех единиц, образующих статистическую совокупность.
Условные обозначения: Р-цена за единицу товара q-количество товаров в натуральном выражении P*q-общая стоимость продукции данного вида Z-себестоимость единицы продукции Z*q-общая себестоимость продукции данного вида Т-общие затраты времени производства продукции W= 1 – подстрочный символ показателя текущего периода 0 – подстрочный показатель базисного периода
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 393; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.190.102 (0.007 с.) |

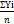

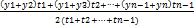


 – произведено продукции данного вида в единицу времени
– произведено продукции данного вида в единицу времени


