
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дипольный момент и изомерия молекул.Содержание книги
Поиск на нашем сайте
Изомерные молекулы независимо от характера изомерии имеют разную равновесную конфигурацию. Следовательно, и разную симметрию. В частности, один изомер может иметь такую симметрию, что его ЭДМ=0, а другой изомер – такую симметрию, что его ЭДМ≠0. Примеры такого рода встречаются как для структурных изомеров, так и для поворотных изомеров (конформеров):
Атомы водорода не указаны
Циклопропан Поворотные изомеры (конформеры) 1,2-дихлорэтана:
Транс-1,2-дихлорэтан
Транс-1,2-дихлорэтилен
До сих пор мы рассматривали молекулы в отсутствии полей. Если молекула помещается в электрическое поле, то изменяется средняя ядерная конфигурация молекулы и распределение электронного заряда в пространстве вокруг ядер. Поэтому момент молекулы в электрическом поле
где
Вектора Если всевозможные ориентации молекулы относительно направления поля считать равновероятными, то средний момент
где а - средняя поляризуемость молекулы. Поскольку деформация молекулы в поле происходит не мгновенно при включении поля, то средняя поляризуемость зависит от частоты, с которой меняется напряженность поля. Если a = a (w0) Размерность поляризуемости определяется из формулы (3.8)
Т.о., поляризуемость a имеет размерность объема и измеряется либо в см3, либо в Å3- кубических ангстремах.
Связь электрических свойств молекул с электрическими свойствами вещества. 3.3.1 Поляризация диэлектриков (связь e и а,m). 3.3.2 Поляризация диэлектрика в переменном поле. 3.3.3 Мольная рефракция (связь n и m).
Поляризация диэлектриков. Одной из важных электрических характеристик (парообразного) вещества, состоящего из молекул определенного строения, являются его диэлектрическая проницаемость e. Между макроскопической характеристикой вещества - его диэлектрической проницаемостью e, с одной стороны, и микроскопическими характеристиками отдельных молекул этого вещества – поляризуемостью а и собственным дипольным моментом m, с другой стороны, может быть установлена определенная зависимость. Мы рассмотрим этот вопрос на основе классической физики. Именно, мы не будем принимать во внимание ни квантование проекции дипольного момента молекулы, ни квантование вращательной энергии молекулы. Также не будем учитывать различий в дипольных моментах отдельных молекул, находящихся в разных электронных, колебательных и вращательных состояниях. Учет всех этих факторов в случае относительно слабых полей и высоких температур (порядка комнатной и выше) приводит в первом приближении к результатам, аналогичным получающимся на основе классической физики. Рассмотрим изменение состояний отдельных молекул и вещества в целом при помещении его в однородное электрическое поле, например в поле плоского конденсатора. Если в отсутствие диэлектрика напряженность в плоском конденсаторе была Е, то при введении между его обкладками диэлектрика напряженность поля Е/ станет меньше в e раз.
Это уменьшение напряженности происходит потому, что диэлектрик поляризуется, то есть на его поверхностях, обращенных к обкладкам конденсатора, появляются избыточные заряды. Плотность зарядов на единицу поверхности, появляющихся на поверхностях, примыкающих к обкладкам конденсатора, обозначим через Р - поверхностная плотность зарядов.
Поляризация диэлектрика в поле объясняется двумя причинами. Во-первых, при помещении в поле в каждой молекуле индуцируется момент
Во-вторых, при помещении в поле молекул, имеющих собственные дипольные моменты
где Рi - поверхностная плотность заряда за счет индуцированного Р0 - за счет ориентации собственных моментов m.. Если выразить Рi и Р0 через микроскопические характеристики а и m и учесть зависимость между Р и e, то можно получить уравнение Ланжевена-Дебая. Уравнение Ланжевена-Дебая для единицы объема вещества.
Где N - число молекул в единице объема, k - постоянная Больцмана, Т - температура,
Если (3.9) умножить на объем одного моля
И учесть, что N1• VM=NA – число Авогадро, то
PM - мольная поляризация.
Уравнение Ланжевена-Дебая для неполярных молекул (m = 0):
|
||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 1106; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.187.60 (0.008 с.) |


 Пропилен
Пропилен 




 Изомеры 1,2-дихлорэтилена
Изомеры 1,2-дихлорэтилена

 3.2 Поляризуемость молекулы
3.2 Поляризуемость молекулы
 (3.7)
(3.7) - момент молекулы в отсутствии поля (собственный дипольный момент),
- момент молекулы в отсутствии поля (собственный дипольный момент), - изменение момента молекулы, происходящее под влиянием поля (наведенный или индуцированный дипольный момент).
- изменение момента молекулы, происходящее под влиянием поля (наведенный или индуцированный дипольный момент). и
и 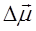 складываются векторно (в общем случае направления не совпадают). Как направлен
складываются векторно (в общем случае направления не совпадают). Как направлен  относительно вектора напряженности электрического поля
относительно вектора напряженности электрического поля 
 ? Направления
? Направления  в общем случае также не совпадают. В отдельном случае, когда вектор
в общем случае также не совпадают. В отдельном случае, когда вектор 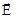 направлен вдоль одной из главных осей поляризуемости, направления векторов
направлен вдоль одной из главных осей поляризуемости, направления векторов  совпадают. Дело в том, что величина и направление дипольного момента зависят от ориентации молекулы относительно внешнего поля
совпадают. Дело в том, что величина и направление дипольного момента зависят от ориентации молекулы относительно внешнего поля  , т.е. существует анизотропия поляризуемости.
, т.е. существует анизотропия поляризуемости. оказывается направленным по направлению поля. Связь между
оказывается направленным по направлению поля. Связь между  выражается формулой:
выражается формулой: (3.8)
(3.8)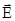 изменяется по закону
изменяется по закону  , то средняя поляризуемость a будет функцией частоты w0:
, то средняя поляризуемость a будет функцией частоты w0: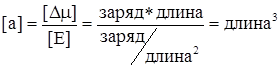

 или
или 
 , который при равновероятных произвольных ориентациях молекул в поле оказывается в среднем направлен по полю. Это происходит потому, что ядра каждой молекулы в среднем смещаются по полю, а электронное облако - против поля и таким образом положительные заряды наведенных диполей в среднем оказываются направленными в сторону отрицательной пластины конденсатора.
, который при равновероятных произвольных ориентациях молекул в поле оказывается в среднем направлен по полю. Это происходит потому, что ядра каждой молекулы в среднем смещаются по полю, а электронное облако - против поля и таким образом положительные заряды наведенных диполей в среднем оказываются направленными в сторону отрицательной пластины конденсатора. , молекулы частично ориентируются по полю, в результате средняя составляющая их собственных моментов оказывается направленной по полю. Поэтому поверхностная плотность зарядов складывается из двух частей:
, молекулы частично ориентируются по полю, в результате средняя составляющая их собственных моментов оказывается направленной по полю. Поэтому поверхностная плотность зарядов складывается из двух частей: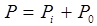 ,
, ,
, (3.9)
(3.9) часто называется удельной поляризацией (на единицу объема)
часто называется удельной поляризацией (на единицу объема)
 (3.10)
(3.10)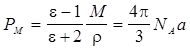 (3.11)
(3.11)


