
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Состояний объектов управления
2.1. Вероятностное описание состояний объектов управления. Характерные неопределенности, встречающиеся в описании состояний ОУ как помехи, условно можно разделить на два класса: вероятностные и нечеткие. Вероятностные помехи различных значений динамических переменных ОУ описываются статистически обоснованными законами распределений вероятности их наступления, или первыми моментами – математическими ожиданиями, дисперсиями. Нечеткие помехи различных значений динамических переменных ОУ задаются лишь диапазонами их значений и некоторыми гипотетическими степенями принадлежности значений этим диапазонам. Случайные события и их вероятности. При испытании (наблюдении, опыте) каждому случайному событию, возможному в данном испытании, приписывают числовые меры его правдоподобия – частость и вероятность. Пусть, например какая-то динамическая переменная S ОУ(например, доход)имеет некоторое частотное распределение wk своих «k»-ых разрядных значений (исходов) при максимальном значении исходов K, как показано на рис. 2.1.1.
Рис. 2.1.1 Естественно, что для построения частот распределений, показанных на рисунке 2.1.1, первоначально необходимо иметь ряд эмпирических данных различных (и не всегда упорядоченных) значений { Sk } исследуемой переменной. Каждому частотному распределению wk по теореме Бернулли может быть поставлена в соответствие эмпирическая или выборочная вероятность или частость wk / wå события «sk», где wå – общее число испытаний (объем выборки). Очевидно, что å Kk wk = wå. При wå ® ¥ выборочная вероятность будет стремиться к теоретической вероятности Prk (сокращенное от Probability). Однако на практике уже при wå @ 300 можно считать, что Prk @ wk / w å = wk /å Kk wk. (2.1.1) Таким образом, под вероятностью PrA события A понимают отношение числа kA случаев, когда это событие наступило при испытании (динамическая переменная S ОУ приняла значение A, т.е. S = A), к общему числу K всевозможных случаев в испытании PrA = kA / K. (2.1.2) Отсюда видно, что для любого события 0 £ Pr (A) £ 1, где вероятность невозможного события (которое никогда не происходит) принимается равной 0, а вероятность достоверного события (которое происходит всегда) принимается равной 1.
При расчете вероятностей событий полезны следующие определения теории вероятностей. Объединением, или суммой событий A и B называют событие С, которое состоит в том, что происходит хотя бы одно из событий A или B (С происходит тогда и только тогда, когда происходит либо A, либо B, либо оба вместе). Объединение событий обозначается как С = A È B, или С = A + B. (2.1.3) Пересечением, или произведением событий A и B называют событие С, которое состоит в том, что происходит оба событий A и B. Пересечение событий обозначается как С = A Ç B или С = A · B или просто С = A B. (2.1.4) Отрицанием события A называют такое событие, которое состоит в том, что A не происходит. Отрицание события обозначается как Если события A и B не могут произойти одновременно, т.е. если AB – невозможное событие, то их называют несовместными. Несовместны, например, события A и Свойства (аксиомы) вероятностей событий: (2.1.5) 1) 0 £ Pr (A) £ 1 для любого (") события A; 2) Pr (достоверного события) = 1, Pr (невозможного события) = 0; 3) Pr (A + B) = Pr (A) + Pr (B) если события A и B – несовместны; 4) Pr (A + B) = Pr (A) + Pr (B) – Pr (AB) в общем случае. Из свойства 4) следует важное свойство, получаемое обращением формулы Pr (A B) = Pr (A) + Pr (B) – Pr (A + B). (2.1.6) Независимые события. События A и B называются независимыми, если Pr (AB) = Pr (A) Pr (B). (2.1.7) Рассмотренные определения легко трактовать с помощью понятий теории множеств и диаграмм Венна (по имени австрийского математика), показанных на рис. 2.1.2. Понятие множества. Множеством называют совокупность определенных различаемых объектов, таких что для любого объекта можно установить принадлежит ли этот объект данному множеству. Примеры: – множество яблок; – множество апельсинов; – множество фруктов = множество яблок + + множество апельсинов. Каждый объект множества может описываться сколь угодно сложным образом с помощью характерных признаков или атрибутов. Из определения множества следует, что объекты могут также описываться и признаками, по которым их различить нельзя. Примеры: – признаки яблок = {цвет; вкус; размер}; – признаки апельсинов = {цвет; вкус; размер}. Очевидно, что во множестве фруктов яблоки нельзя отделить от апельсинов лишь по признаку «размер».
Если объект принадлежит множеству, то он является элементом данного множества. Существует несколько общепринятых способов записей множеств: X = { x 1, x 2, … xN }, где X – множество, содержащее элементы x 1, x 2, … xN; X = { x: x – целое число и 6 < x < 10}, где X – множество всех x таких, что они все целые и заключены в пределах (6 ¸ 10); X = {7, 8, 9, 10, 11}, где X – упорядоченное множество пяти натуральных чисел; X = {1, 8, 2, 10}, где X – неупорядоченное множество четырех натуральных чисел. Из определения множества следует, что запись X = {6, 6, 6, 6} не описывает множество, т.к. не ясно как различать элементы. В то же время, запись «множество теннисных мячей в сумке = { мяч 1, мяч 2, … мяч 10}» описывает множество, так как каждый мяч занимает свою пространственную позицию и легко различается. Мощностью множества A называется количество N составляющих его элементов. Обозначается как NA или ú A ú. Простейшие операции над множествами. Объединение («È» или «+»): A È B = { x: x Î A или x Î B }, где «Î» – символ (квантор) принадлежности; Пересечение («Ç» или «·»): A Ç B = { x: x Î A и x Î B }.
Примеры: {1, 2} È {2, 3} = {1, 2, 3}; {1, 2} Ç {2, 3} = {2}; Разность множеств («\»): A \ B = { x: x Î A и x Ï B }, где «Ï» – квантор не принадлежности. Запись A \ B читается также, как «дополнение B до A». Пример: если A = {1, 2, 3}, B = {2, 3, 4}, то A \ B = {1}. Симметрическая разность множеств («D»): A D B = (A È B) \ (A Ç B); A D B º B D A. Примеры: если A = {1, 2, 3}, B = {2, 3, 4}, то A D B = {1, 2, 3, 4}\ {2, 3} = {1, 4}; если A – множество товаров, доступных менеджеру M 1, B – множество товаров, доступных менеджеру M 2, то A È B – множество товаров, доступных или M 1 или M 2, A Ç B – множество товаров, доступных M 1 и M 2, A \ B – множество товаров, доступных только M 1, B \ A – множество товаров, доступных только M 2, A D B – множество товаров, доступных только одному из менеджеров. Универсальное множество E – множество всех рассматриваемых в данной задаче элементов. Пустое множество Æ – множество не содержащее ни одного элемента. Например, {1, 2} Ç {3, 4} = Æ. Отсюда следует, что два множества A и B не пересекаются, если A Ç B = Æ. Дополнением множества A является множество A’ = E \ A = { x: x Î A }. Отсюда следует, что A È A’ = E и A Ç A’ = Æ.
Диаграммы Венна для множеств (рис. 2.1.2):
Универсальное множество. Множества А, B.
Множество А È B. Множество А Ç B.
Множество B’ Ç C. Множество A È (B’ Ç C). Рис. 2.1.2 Подмножества. A Í B ‑ множество A является подмножеством множества B, если из x Î A ® x Î B,где«®» ‑ символ «следует». A Ì B ‑ множество A является собственным подмножеством множества B, если существует x Î B такой, что x Ï A. Примеры: если A = множество всех яблок = {анис, антоновка, мельба, …}, С = множество всех фруктов, то A Í С; если A = множество вех яблок = {анис, антоновка, мельба, …}, B = множество всех цитрусовых = = {апельсин, лимон, …}, С = множество всех фруктов, то A + + B Í C, а A Ì C и B Ì C. На диаграмме Венна подмножества изображаются в виде рис. 2.1.3.
Рис. 2.1.3 Сочетательные правила алгебры множеств:
A Ç (B È C) = (A Ç B) È (A Ç C), A · (B + C) = A · B + A · C. Правила де’ Моргана: (A Ç B) ’ = A’ + B’, (A È B) ’ = A’ Ç B’. Степень множества ‑ множество всех подмножеств данного множества. Обозначение – P (A). Например, если A = {1, 2, 3}, то P (A) = { Æ, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2,3}}. P (A)ú = 23 = 8. Покрытие множества ‑ A =
Рис. 2.1.4.
Произведение множеств. Если A = { a, b, c, d, …}, а B = {1, 2, 3, …}, то произведение множеств определяется как A ´ B = { a 1, a 2, a 3, …, b 1, b 2, b 3, …, c 1, c 2, c3, …}. Широко известным примером рассмотренного произведения множеств букв и цифр является совокупность квадратов, покрывающих шахматную доску. Если добавить множество шахматных фигур С = { фб 1, фб 2, …, фб 8, фч 1, фч 2, …, фч 8}, то произведением множеств A ´ B ´ С = { фб 1 a 2, фб 2 b 4, … }будет множество всевозможных игровых позиций ‑ положений фигур, сформированных с учетом правил ходов фигур и их начальных позиций. В общем случае справедливо правило A ´ B ¹ B ´ A. Действительно, пусть A = {0, 1}, B = { x, y). Тогда A ´ B = {(0, x), (0, y), (1, x), (1, y)}, B ´ A = {(x, 0), (x, 1), (y, 0), (y, 1)}. Множественные произведения записывают в виде A ´ A ´ A ´ A ´ A ´ A … = A n, A1 ´ A2 ´ A3 ´ … ´ An = Отношения на множествах. Отношением «R» – го типа или просто отношением R на множествах A и B (записывается как ARB) называется «R»-ое подмножество прямого произведения A ´ B множеств A и B. Отношения на множествах A и B являются бинарными или парными отношениями. По аналогии с такими отношениями легко ввести отношения на множествах A и B и C (триарные отношения), A и B и C и D (четыреарные отношения) и т.д.. Любое отношение устанавливает определенную связь между элементами множеств. Для парных отношений такая связь может быть описана с помощью рис. 2.1.5.
Рис. 2.1.5
В отношениях выделяют области определения и области значений, устанавливая тем самым несимметричную связь между элементами множеств, входящих в отношения X (R) = { x: x Î A, (x, y) Î R } ‑ область определения отношения R включает все элементы множества A, входящие в множество ARB; Y (R) = { y: y Î B, (x, y) Î R } ‑ область значений отношения R включает все элементы множества B, входящие в множество ARB.
Пример: множество родителей = A = {Иванов И.И., Иванова А.А., Петров П.П., Петрова В.В.},
множество детей = B = {Иванов С.И., Петрова Г.П.}. Семья Ивановых описывается отношением R 1
Семья Петровых описывается отношением R 2
Отношения можно описывать также с помощью направленных графов. Так, например, если X = { x 1, x 2, x 3, x 4}, а Y = { y 1, y 2, y3, y4), то отношение XRY = {(x 1, y 1), (x 1, y 4), (x 4, y 2)} можно изобразить, как показано на рис. 2.1.6.
Рис. 2.1.6
Функции и отображения множеств. Если между X и Y установлено однозначное отношение f, то это отношение является функцией или функциональным отношением. Функциональное отношение X f Y записывается как y = f (x) или f: X ® Y. Функция f: X ® Y является отображением, если ее область определения совпадает с X.
Примеры: 1) Товары и цены (см. рис. 2.1.7): Товары = X = {телевизор Sony, магнитофон Panasonic, фотокамера Samsung }, Цены = Y = {$500, $200, $2000},
Рис. 2.1.7
2) Образы (см. рис. 2.1.8 а, б, в):
Рис. 2.1.8 а
Рис. 2.1.8 б
Рис. 2.1.8 в
Алгебра событий (теоремы сложения и умножения). Алгебра событий строится путем их отождествления с элементами множеств. Сложения вероятностей – вероятность объединения множеств: Несовместные события (рис.2.1.9):
Рис.2.1.9 Pr ( Pr ( Очевидно, что если Пример: пусть E = множество фруктов = {апельсины, бананы, яблоки}. При этом известно количество фруктов каждого сорта, как показано на рис. 2.1.10. Необходимо найти вероятности появления фруктов каждого сорта при их выборке по отдельности и в парных сочетаниях.
апельсины бананы яблоки Рис. 2.1.10 Очевидно, что Pr ( Совместные события (рис. 2.1.11 и 2.1.12):
Рис. 2.1.11 Pr (A + B) = Pr (A) + Pr (B) – Pr (AB). (2.1.9)
Рис. 2.1.12
Pr (A + B + С) = Pr ((A + B) + С) = (2.1.10) = Pr (A + B) + Pr (C) – Pr ((A + B) C) = = Pr (A) + Pr (B) – Pr (AB) + Pr (C) – – Pr (A C + B C) = Pr (A) + Pr (B) + Pr (C) – – Pr (AB) – Pr (A C) – Pr (B C) + Pr (ABC). Применяя (2.1.9) и (2.1.10) к общему случаю, получим Pr ( + + (-1) K- 1 Pr (A1A2 … AK). (2.1.11) Умножение вероятностей. Pr (A B) = Pr (A) Pr (B ÷ A), где Pr (B ÷ A) ‑ условная вероятность события B, Pr (B A) = Pr (B) Pr (A ÷ B), где Pr (A ÷ B) ‑ условная вероятность события A. Если события A и B независимы, то Pr (B ÷ A) = Pr (B) и Pr (A ÷ B) = Pr (A), а Pr (A B) = Pr (A) Pr (B). В общем случае для независимых событий Ak справедливо Pr ( В общем случае для зависимых событий справедливо Pr (A 1 A 2 … AK) = Pr (A 1) Pr (A 2÷ A 1) Pr (A 3÷ A 1 A 2) Pr (A 4÷ A 1 A 2 A 3) … Pr (AK ÷ A 1 A 2 … AK-1). (2.1.13)
2.2. Вероятностное описание объектов управления при однократных опытах. Формулы Байеса. Так как Pr (A B) = Pr (B A), то Pr (A) Pr (B ÷ A) = Pr (B) Pr (A ÷ B). Следовательно справедливы формулы (Байеса) Pr (B ÷ A) = Pr (B) Pr (A ÷ B) / Pr (A), (2.2.1) Pr (A ÷ B) = Pr (A) Pr (B ÷ A) / Pr (B). Пример 2.2.1: предприятие производит N = x + y + z + w автомобилей с различными двигателями и кузовами, как показано в таблице 2.2.1. Таблица 2.2.1
Какова вероятность покупки автомобиля с кузовом типа C при условии, что двигатель будет типа А? Решение: используя понятие частости событий и формулы Байеса (2.2.1) получим Pr (С ÷ A) = Pr (С ÷ A) = Pr (С) Pr (A ÷ С) / Pr (A) = Формула полной вероятности. Пусть событие A происходит вместе (совместно) с одним из событий Г 1, Г 2, …, ГK, образующих полную группу несовместных событий. Напомним, что для полной группы несовместных событий справедливо
Pr ( Будем называть такие события гипотезами, а вероятности Pr (Гk) – априорными вероятностями гипотез. Тогда возможно определить полную вероятность наступления события A Pr (A) º Pr (A Г1 + A Г2 + …+ A ГN) = (2.2.3) =
Пример 2.2.2: фирма управляется двумя менеджерами. Предположим, что при работе двух менеджеров отрицательные эффекты происходят с вероятностью q 12, 1-го менеджера – с вероятность q 1, 2-го менеджера – с вероятность q 2, при отсутствии менеджеров – с вероятностью q 0. Пусть 1-ый менеджер имеет частоту принятия верных решений по парированию отрицательных эффектов p 1, 2-ой ‑ p 2. Все отрицательные эффекты независимы друг от друга. Найти вероятность парирования отрицательных эффектов в фирме. Решение: рассмотрим гипотезы Г 12 ‑ работают оба менеджера; Г 1 ‑ работает лишь 1-ый менеджер; Г 2‑ работает лишь 2-ой менеджер; Г 0‑ ни один из менеджеров не работает. Введем событие A, как парирование отрицательных эффектов в фирме. Тогда Pr (Г 12) = p 1 p 2; Pr (A ú Г 12) = 1 - q 12; Pr (Г 1) = p 1 (1- p 2); Pr (A ú Г 1) = 1 - q 1; Pr (Г 2) = p 2 (1- p 1); Pr (A ú Г 2) = 1 - q 2; Pr (Г 0) = (1- p 1) (1- p 2); Pr (A ú Г 0) = 1 – q 0. Используя формулу (2.2.3), получим Pr (A) = Pr (Г 12) Pr (A ú Г 12) + Pr (Г 1) Pr (A ú Г 1) + + Pr (Г 2) Pr (A ú Г 2) + Pr (Г 0) Pr (A ú Г 0) = = p 1 p 2 (1 - q 12) + p 1 (1- p 2) (1 - q 1) + + p 2 (1- p 1) (1 - q 2) + (1- p 1) (1- p 2) (1 – q 0).
Полная формула Байеса. Как изменятся априорные вероятности гипотез Pr (Гk) после опыта, в результате которого наблюдается событие A? Заменяя в формуле Байеса (2.2.1) B на Гk и используя (2.2.3), получим апостериорную вероятность (вероятность после опыта) Pr (Гk ÷ A) = Pr (Гk) Pr (A ÷ Гk) / Пример2.2.3: на рынок поставляются приборы (стиральные машины). Известно, что 40% из них собираются из высококачественных деталей. Для приборов, собранных из высококачественных деталей, вероятность безотказной работы за время гарантии – 95%. Для приборов, собранных из обычных деталей, вероятность безотказной работы за время гарантии – 70%. Фирма закупила прибор и испытала его в течении времени гарантии. Прибор работал безотказно. Какова вероятность того, что прибор собран из высококачественных деталей? Решение: введем гипотезы Г 1 ‑ прибор собран из высококачественных деталей; Г 2 ‑ прибор собран из обычных деталей. Априорные вероятность гипотез до опыта: Pr (Г 1) = 0,4; Pr (Г 2) = 0,6. Пусть A – событие безотказной работы в течение времени гарантии. Тогда Pr (A ú Г 1) = 0,95; Pr (A ú Г 2) = 0,7. Следовательно, на основании (2.2.3) получим Pr (Г 1 ÷ A) = = Отсюда видно, что испытание повысило вероятность априорной гипотезы. Пример2.2.4: два брокера на бирже независимо друг от друга делают ставки. Вероятность выигрыша для 1-го – 80%, для 2-го – 40%. Обнаружен выигрыш одного из них. Каковы апостериорные вероятности выигрышей брокеров? Решение: примем за A событие выигрыша одним из брокеров и введем априорные вероятности Г 0 ‑ оба брокера проиграли; Pr (Г 0) = 0,2 * 0,6 = 0,12; Г 12 ‑ оба выиграли; Pr (Г 12) = 0,8 * 0,4= 0,32; Г 1 ‑ выиграл 1-ый; Pr (Г 1) = 0,8 * 0,6= 0,48; Г 2 ‑ выиграл 2-ой; Pr (Г 2) = 0,4 * 0,2= 0,08; Pr (A ú Г 0) = 0; Pr (A ú Г 12) = 0; Pr (A ú Г 1) = 1; Pr (A ú Г 2) = 1. Pr (Г 1 ÷ A) = Pr (Г 2 ÷ A) = Таким образом, факт выигрыша повышает шанс выигрыша брокера, обладающего большей квалификацией. Пример2.2.5: фирма-производитель утверждает, что надежность ее оборудования – 98%. Заказчик назначает аудитора (эксперта) и тот утверждает, что надежность ‑ 90%. Заказчик сам считает, что заявление изготовителя верно на 40%, а эксперта ‑ на 60%. Далее заказчик проводит испытание двух единиц оборудования. Если оба испытания неудачны, то каково будет мнение заказчика о производителе и эксперте? Решение: примем за A событие двух неудач; Г 1 ‑ прав производитель; Pr (Г 1) = 0,4; Г 2 ‑ прав эксперт; Pr (Г 2) = 0,6; Pr (A ú Г 1) = 0,02 *0,02 = 0,0004; Pr (A ú Г 2) = 0,1 *0,1= 0,01. Тогда Pr (A) = Pr (Г 1) Pr (A ú Г 1) + Pr (Г 2) Pr (A ú Г 2) = = 0,4*0,0004 + 0,6*0,01 = 0,00616; Pr (Г 1 ÷ A) = Pr (Г 2÷ A) =
2.3. Вероятностное описание объектов управления при повторении опытов. Пусть производятся сделки с различными фирмами. Результатом каждой сделки может быть некоторое событие A (успех). Нас интересует общее число успехов. В общем случае говорят, что производят несколько опытов, приводящих к событию A в каждом из них. Необходимо уметь определять вероятность любого заданного числа появления события A в результате серии опытов. Частная теорема и повторение опытов. Задача решается наиболее просто, когда опыты являются независимыми. Например, мы выбрали наугад несколько магазинов Москвы и хотим купить один и тот же товар. Если все данные магазины получают товар от различных поставщиков (с различных баз), то наши опыты независимы. Вероятность того или иного исхода каждого из опытов не зависит от того, какие исходы имели другие опыты. В этом случае вероятность события A во всех опытах одинакова – Pr (A) = p. Пример 2.3.1: проводятся переговоры о заключении сделки с тремя фирмами. Вероятность заключения сделки – p. Найти вероятность того, что мы заключим хотя бы две сделки. Решение: обозначим: B 23 – событие заключения двух сделок в трех опытах; A 1 – событие заключения сделки с 1-ой фирмой; A 2 – событие заключения сделки со 2-ой фирмой; A 3 – событие заключения сделки с 3-ей фирмой. Событие B 23 (заключения двух сделок в трех опытах) может произойти тремя независимыми способами (вариантами), как показано на рис. 2.3.1: 1) сделка A 1, сделка A 2, не заключение сделки 2) сделка A 1, не заключение сделки 3) не заключение сделки
Рис. 2.3.1 Следовательно: B 23 = A 1 A 2 Так как все три варианта несовместимы, а события A 1, A 2 и A 3 независимы, то Pr (B 23) = Pr (A 1 A 2 = pp (1 – p) + p (1 – p) p + (1 – p) p p. Обозначая 1 – p = q, получим Pr (B23) = 3 p 2 q. (2.3.1) Пример 2.3.2: производится «N» независимых опытов, в каждом из которых может появиться или не появиться некоторое событие A. Вероятность появления события A – Pr (A) = p, а вероятность не появления – q = 1 – p. Требуется найти вероятность PrMN (A) того, что событие A в этих «N» опытах появится ровно «M» раз. Решение: используя технику примера 2.3.1, получим BMN = A 1 A 2 … AM + A 1 + В каждом слагаемом (2.3.2) событие A входит «M» раз, а
(2.3.3)
где В связи с тем, что вероятность Pr (BMN) в (2.3.3) по форме представляет собой члены разложения бинома (q + p) N = распределение вероятности Pr (BMN) называют биномиальным распределением. Общая теорема и повторение опытов. Пусть вероятность появления события A в «i»-ом опыте – pi, а вероятность не появления – qi = (1- pi), где i = 1, 2, …, N). Запись BMN = A 1 A 2 … AM + A 1 описывает событие, состоящее в том, что событие A появилось «M» раз в «N» опытах. Тогда Pr (BMN) = p 1 p 2… pM qM+ 1 … qN + … + + p 1 q 2 p 3 … qN- 1 pN + …. (2.3.5) Для расчета вероятности Pr (BMN) вводят вспомогательную, так называемую, производящую функцию jN (z) = (q 1 + p 1 z) (q 2 + p 2 z) … (qN + pN z) = = Оказывается, что все коэффициенты PmN данной функции в точности равны вероятностям Pr (BmN) появления события A ровно «m» раз в «N» опытах Для частного случая, когда все pi = p jN (z) = (q + p z) (q + p z) … (q + p z) = = (q + p z) N = Отметим условие
которое следует из определения jN (z) при z º 1 (так как qi + pi = = 1) и из того, что события B0N, B1N, B2N, …, BNN образуют полную группу несовместных событий (так как PmN – вероятность появления события A «m» раз в «N» опытах). Групповые события. Обозначим CMN событие, состоящее в том, что событие A появится не менее «M» раз в «N» опытах. Очевидно, что CMN = BMN + BM+ 1 N + … + BNN, Pr (CMN) = Pr (BMN) + Pr (BM+ 1 N) + …+ Pr (BNN) = = Пример2.3.3: проводится 4-ре независимых переговоров с 4-мя фирмами о заключении одного и того же соглашения (A). Вероятности заключения соглашения: p 1 = 0,1; p 2 = 0,2; p 3 = 0,3; p 4 = 0,4. Найти вероятности: P 04 – вероятность ни одного соглашения; P 14 – вероятность одного соглашения; P 24 – вероятность двух соглашений; P 34– вероятность трех соглашений; P 44 – вероятность четырех соглашений. Решение: воспользуемся производящей функцией из (2.3.7) j 4(z) = (q 1 + p 1 z) (q 2 + p 2 z) (q 3 + p 3 z) (q 4 + p 4 z) = = (0,9 + 0,1 z) (0,8 + 0,2 z) (0,7 + 0,3 z) (0,6 + 0,4 z) = = 0,302 + 0,440 z + 0,215 z 2 + 0,040 z 3 + 0,002 z 4. Таким образом P 04 = 0,302; P 14 = 0,440; P 24 = 0,215; P 34 = 0,040; P 44 = 0,002. Пример2.3.4: при поиске делового партнера среди всех возможных менеджер 4-ре раза обратился к одной и той же фирме по телефону. Вероятность телефонной связи с этой фирмой при каждом обращении равна p = 0,3 (3 связи при 10-ти звонках). Известно также, что для успешного заключения контракта достаточно двух переговоров с фирмой. При однократном переговоре вероятность заключения контракта равна 0,6. Найти вероятность события A – заключения контракта с фирмой. Решение: выдвинем две гипотезы: Г 0 – связь с фирмой не состоялась; Г 1– связь с фирмой состоялась 1 раз. Рассчитаем вероятность Pr ( Pr ( Pr (Г 0) = P 04 = (1- p)4 = (0,7)4 = 0,240; Pr (Г 1
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 382; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.120.159 (0.302 с.) |

 .
.


 Множество А’. Множества А, B, C.
Множество А’. Множества А, B, C.
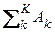 , где Ak Ç Am = Æ для k ¹ m. Покрытие разбивает любое множество A на непересекающиеся подмножества Ak.
, где Ak Ç Am = Æ для k ¹ m. Покрытие разбивает любое множество A на непересекающиеся подмножества Ak. На диаграмме Венна покрытия изображаются в виде рис. 2.1.4.
На диаграмме Венна покрытия изображаются в виде рис. 2.1.4. .
.







 ) =
) =  или
или ) =
) = 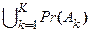 . (2.1.8)
. (2.1.8)
 +
+  ) = Pr (
) = Pr (

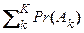 –
– 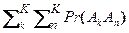 +
+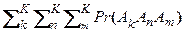 – … +
– … +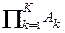 )= Pr (
)= Pr ( )=
)=  , (2.1.12)
, (2.1.12) ,
, .
. = E, (2.2.2)
= E, (2.2.2) =
=  = 1.
= 1.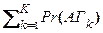 =
=  .
. =
= = 0,475.
= 0,475. = 6/7 = 86%,
= 6/7 = 86%,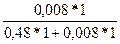 = 1/7 = 14%.
= 1/7 = 14%. = 0,03;
= 0,03; = 0,97.
= 0,97. ;
;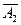 ; сделка A 3;
; сделка A 3; , сделка A 2, сделка A 3.
, сделка A 2, сделка A 3.
 A 2 A 3.
A 2 A 3.
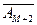 …
… 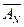 +
+ AN +
AN +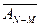
 … AN. (2.3.2)
… AN. (2.3.2)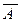 – «N - M» раз. Тогда
– «N - M» раз. Тогда
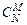 =
=  – число сочетаний из N по M.
– число сочетаний из N по M. , (2.3.4)
, (2.3.4) =
= 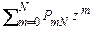 . (2.3.6)
. (2.3.6) . (2.3.7)
. (2.3.7) = 1, (2.3.8)
= 1, (2.3.8)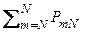 = 1 -
= 1 - 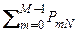 . (2.3.9)
. (2.3.9)


