
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ранг матрицы. Элементарные операции с матрицей.
Ранг матрицы Строки и столбцы матрицы являются элементами соответствующих векторных пространств:
Рангом матрицы называют количество линейно независимых столбцов матрицы (столбцовый ранг матрицы) или количество линейно независимых строк матрицы (строчный ранг матрицы). Этому определению эквивалентно определение ранга матрицы как порядка максимального отличного от нуля минора матрицы. При элементарных преобразованиях ранг матрицы не меняется. Свойства линейных операций: Везде далее матрицы 1. Ассоциативность 2. 3. 4. Коммутативность 5. Дистрибутивность 6. 7. Теорема о базисном миноре. В произвольной матрице каждый столбец (строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор. ОПРЕДЕЛЕНИЕ В матрице минор порядка Следствие. Определитель -го порядка равен нулю тогда и только тогда, когда его строки (столбцы) линейно зависимы. Теорема о базисном миноре матрицы служит для доказательства таких важных теорем: Теорема 1. Линейно независимые строки (столбцы) матрицы, количество которых равно рангу матрицы, являются базисными строками (столбцами). Теорема 2. (Теорема о ранге матрицы). Для любой матрицы ее ранг равен максимальному количеству ее линейно независимых строк (столбцов). Критерий совместности СЛАУ Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:
Для того, чтобы линейная система являлась совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу ее основной матрицы.
Доказательство (условия совместности системы) Необходимость Пусть система совместна. Тогда существуют числа Достаточность Пусть Следствия
Решение СЛАУ общего вида. Основная запись СЛАУ. Понятие решения СЛАУ и некоторые определения.В общем случае основная запись системы n линейных алгебраических уравнений с n неизвестными имеет следующий вид:
При этом через Система называется однородной, если все ее свободные члены Если хотя бы один из свободных членов Решением системы называется такая совокупность Система уравнений вида называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее не существует ни одного решения. Совместная система вида называется определенной, если она имеет единственное решение.
Совместная система вида называется неопределенной, если у нее существуют по крайней мере два различных решения.
Краткая запись СЛАУ:
Матричная формулировка СЛАУ:
где
Представление с помощью расширенной матрицы.В действительности, система уравнений полностью определяется элементами матрицы и вектора правой части. Обозначения неизвестных имеют чисто символический смысл. При различных допустимых преобразованиях системы также меняются только значения элементов матрицы и правой части. Поэтому вполне достаточным представлением системы уравнений является, так называемая, расширенная матрица (она получается из матрицы коэффициентов системы путем добавления к этой матрице столбца свободных членов):
где Прямые методами решения СЛАУ называются методы, которые позволяют получить теоретически точное (с учетом ограниченности разрядной сетки ЭВМ) решение за конечное число операций. Прямым методом является, в частности, метод Гаусса, Решение однородной СЛАУ. Любая однородная СЛАУ имеет хотя бы одно решение – нулевое (его ещё называют тривиальное), в котором все переменные равны нулю. Подставим, например, x 1=0, x 2=0, x 3=0 и x 4=0 в записанную выше систему. Получим два верных равенства: {2⋅0−3⋅0−0−0=0;−4⋅0+5⋅0+3⋅0=0. Однако следствие из теоремы Кронекера-Капелли однозначно указывает на то, что если СЛАУ имеет решение, то есть только два варианта. Либо это решение единственно (и тогда СЛАУ называют определённой), либо этих решений бесконечно много (такую СЛАУ именуют неопределённой). С однородными СЛАУ связано дополнительное понятие – фундаментальная система решений. Дело в том, что если ранг матрицы системы однородной СЛАУ равен r, то такая СЛАУ имеет n − r линейно независимых решений: φ 1, φ 2,..., φn − r. Любая совокупность n − r линейно независимых решений однородной СЛАУ называется фундаментальной системой (или совокупностью) решений данной СЛАУ. Часто вместо словосочетания "фундаментальная система решений" используют аббревиатуру "ФСР". Если решения φ 1, φ 2,..., φn − r образуют ФСР, и X – матрица переменных данной СЛАУ, то общее решение СЛАУ можно представить в таком виде: X = C 1⋅ φ 1+ C 2⋅ φ 2+…+ Cn − r ⋅ φn − r, где C 1, C 2,..., Cn − r – произвольные постоянные. Метод Гаусса классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы
|
|||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.154.208 (0.01 с.) |
 составляют элементы пространства размерности
составляют элементы пространства размерности  ;
;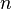 .
. ,
,  и
и  - матрицы одного размера.
- матрицы одного размера.
 , где
, где  - нулевая матрица соответствующего размера.
- нулевая матрица соответствующего размера.




 называется базисным, если он не равен нулю, а все миноры порядка и выше равны нулю или не существуют вовсе, т.е. совпадает с меньшим из чисел или.
называется базисным, если он не равен нулю, а все миноры порядка и выше равны нулю или не существуют вовсе, т.е. совпадает с меньшим из чисел или. такие, что
такие, что  . Следовательно, столбец
. Следовательно, столбец  является линейной комбинацией столбцов
является линейной комбинацией столбцов  матрицы
матрицы  .
.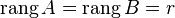 . Возьмем в матрице
. Возьмем в матрице  , то он же и будет базисным минором и матрицы
, то он же и будет базисным минором и матрицы  . Тогда, согласно теореме о базисном миноре, последний столбец матрицы
. Тогда, согласно теореме о базисном миноре, последний столбец матрицы  (2.2.1)
(2.2.1) обозначены неизвестные, подлежащие определению; величины
обозначены неизвестные, подлежащие определению; величины  называемые коэффициентами системы, и величины
называемые коэффициентами системы, и величины  , называемые свободными членами, предполагаются известными. Каждый коэффициент системы
, называемые свободными членами, предполагаются известными. Каждый коэффициент системы  имеет два индекса, первый из которых
имеет два индекса, первый из которых  указывает номер уравнения, а второй
указывает номер уравнения, а второй  номер неизвестного, при котором стоит этот коэффициент.
номер неизвестного, при котором стоит этот коэффициент. равны нулю.
равны нулю. отличен от нуля, то система называется неоднородной.
отличен от нуля, то система называется неоднородной. чисел
чисел 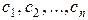 , которая при подстановке в систему на место неизвестных
, которая при подстановке в систему на место неизвестных  . (2.2.2)
. (2.2.2) , (2.2.3)
, (2.2.3) ; (2.2.4)
; (2.2.4) – матрица коэффициентов системы;
– матрица коэффициентов системы;  – вектор неизвестных;
– вектор неизвестных;  – вектор свободных членов.
– вектор свободных членов. (2.2.5)
(2.2.5) .
.


