
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Следствия из второго замечательного предела.
1. 2. 3. Натуральный логарифм и гиперболические функции. Определение 14.2. Логарифм с основанием е называется натуральным логарифмом. Обозначение: log ex =ln x. Определение 14.3. Функции Замечание 1. Гиперболические функции обладают некоторыми свойствами, похожими на свойства обычных тригонометрических функций. Например, сh² x – sh² x = ¼( e 2 x + 2 + e -2 x - e 2 x + 2 - e -2 x )=1, 2 sh x ch x = 2 th x =sh x /ch x, cth x =ch x /sh x , th x ·cth x = Замечание 2. Термин «гиперболические» объясняется тем, что уравнения x = a ch t, y = a sh t, a >0, являются параметрическими уравнениями правой ветви гиперболы x ² - y ² = a ², так же, как x = a cos t, y = a sin t (0≤ t ≤2π) – параметрические уравнения окружности x ²+ y ²= a ².
Лекция 15. Сравнение бесконечно малых. Символы «о» и «О». Эквивалентные бесконечно малые, их применение к вычислению пределов. Бесконечно большие функции и их связь с бесконечно малыми. Рассмотрим функции α(х ) и β(х), для которых 1. Если 2. Если 3. Если Обозначения: α(х)=О(β(х)) – бесконечно малые одного порядка, α(х)~β(х ) – эквивалентные бесконечно малые, α(х)=о(β(х)) – α есть бесконечно малая более высокого порядка, чем β . Замечание 1. Используя 1-й и 2-й замечательные пределы и их следствия, можно указать бесконечно малые функции при х →0, эквивалентные х: sin x, tg x, arcsin x, arctg x, ln(1+ x ), ex -1. Замечание 2. При раскрытии неопределенности вида Пример.
Бесконечно большие функции. Определение 15.1. Функция f(x) называется бесконечно большой при х
Для бесконечно больших можно ввести такую же систему классификации, как и для бесконечно малых, а именно:
1. Бесконечно большие f(x ) и g(x ) считаются величинами одного порядка, если
2. Если 3. Бесконечно большая f(x ) называется величиной k -го порядка относительно бесконечно большой g(x ), если Замечание. Отметим, что ах – бесконечно большая (при а >1 и х Теорема 15.1. Если α(х ) – бесконечно малая при х→х0, то 1/ α(х ) – бесконечно большая при х→х0 . Доказательство. Докажем, что |1/ α(x )|> M. Значит, Лекция 16. Непрерывность функции в точке. Локальные свойства непрерывных функций. Непрерывность сложной и обратной функций. Непрерывность элементарных функций. Точки разрыва функций и их классификация. Свойства функций, непрерывных на отрезке: ограниченность, существование наибольшего и наименьшего значений, промежуточные значения. Определение 16.1. Функция y=f(x ) называется непрерывной в точке х0, если
Замечание. Из этого определения следует, во-первых, что функция определена при х = = х0, и во-вторых, что при х→х0 существует конечный предел функции.
|
|||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 340; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.179.186 (0.005 с.) |

 где a > 0, y = ax - 1.
где a > 0, y = ax - 1.
 (гиперболический синус),
(гиперболический синус),  (гиперболический косинус),
(гиперболический косинус),  (гиперболический тангенс) и
(гиперболический тангенс) и  (гиперболический котангенс) называются гиперболическими функциями.
(гиперболический котангенс) называются гиперболическими функциями.
 =
=  =sh2 x ,
=sh2 x ,
 =1 и т.д.
=1 и т.д.
 то есть бесконечно малые в окрестности х0 .
то есть бесконечно малые в окрестности х0 . то α(х ) и β(х )называются бесконечно малыми одного порядка. В частности, если А =1, говорят, что α(х ) и β(х ) – эквивалентные бесконечно малые.
то α(х ) и β(х )называются бесконечно малыми одного порядка. В частности, если А =1, говорят, что α(х ) и β(х ) – эквивалентные бесконечно малые. то α(х ) называется бесконечно малой более высокого порядка по сравнению с β(х ).
то α(х ) называется бесконечно малой более высокого порядка по сравнению с β(х ). , то α(х ) есть бесконечно малая порядка n по сравнению с β(х).
, то α(х ) есть бесконечно малая порядка n по сравнению с β(х).  , то есть предела отношения двух бесконечно малых, можно каждую из них заменять на эквивалентную – эта операция не влияет на существование и величину предела.
, то есть предела отношения двух бесконечно малых, можно каждую из них заменять на эквивалентную – эта операция не влияет на существование и величину предела.
 х0, если
х0, если
 .
. , то f(x ) считается бесконечно большой более высокого порядка, чем g(x).
, то f(x ) считается бесконечно большой более высокого порядка, чем g(x). 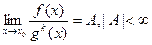 .
.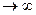 ) более высокого порядка, чем xk для любого k, а log ax – бесконечно большая низшего порядка, чем любая степень хk .
) более высокого порядка, чем xk для любого k, а log ax – бесконечно большая низшего порядка, чем любая степень хk .
 при | x - x0 | < δ. Для этого достаточно выбрать в качестве ε 1/ M. Тогда при | x - x0 | < δ | α(x)|< 1/ M, следовательно,
при | x - x0 | < δ. Для этого достаточно выбрать в качестве ε 1/ M. Тогда при | x - x0 | < δ | α(x)|< 1/ M, следовательно,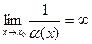 , то есть 1/ α(х ) – бесконечно большая при х→х0.
, то есть 1/ α(х ) – бесконечно большая при х→х0. 



