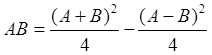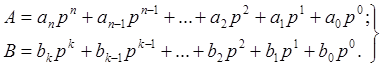Давньоєгипетський спосіб множення, що вважається одним iз найбільш древніх, оснований на використанні операції подвоєння.

Незважаючи на те, що в давньоєгипетському способi використову-ються елементи двійкового множення, числа-множники можуть бути початково представленi в системі числення з будь-якою основою р > 2.

Для р = 2, давньоєгипетський спосiб множення спiвпадає зi звичайним двійковим множенням методом накопичення сум часткових добутків.

У випадку застосування давньоєгипетського способу множення до деяких двох чисел В та А, щодо них здiйснюються наступнi дії:

1) обчислюють усі можливі значення 2 ⁱ і В *2 ⁱ (i = 0, 1, 2,.., k) доти, поки не буде виконано умову 2 ^{k+ 1} > А;

2) значення А представляють у вигляді поліному з основою 2 (визначають у вигляді суми значень двійок у відповідних ступенях);

3) добуток одержують додаванням значень В *2 ⁱ для тих i, що входять до визначення числа А.

Розглянемо реалiзацiю алгоритму давньоєгипетського способу множення на прикладi знаходження добутку чисел В = 154 та А = 23.

Етап1. Будемо обчислювати всі можливі значення 2 ⁱ (i = 0, 1, 2,.., k) і 154 *2 ⁱ доти, поки не буде виконано умову 2 ^{k+ 1} > 23.

Крок 1.1: i = 0, 154*2⁰ = 154*1 = 154, i + 1 = 1, умову 2¹ = 2 > 23 не виконано, а тому продовжуємо здiйснювати обчислення далi.

Крок 1.2: i = 1, 154*2¹ = 154*2 = 308, i + 1 = 2, умову 2² = 4 > 23 не виконано, а тому продовжуємо здiйснювати обчислення далi.

Крок 1.3: i = 2, 154*2² = 308*2 =616, i + 1 = 3, умову 2³ = 8 > 23 не виконано, а тому продовжуємо здiйснювати обчислення далi.

Крок 1.4: i = 3, 154*2³ = 616*2 = 1232, i + 1 = 4, умову 2⁴ = 16 > 23 не виконано, а тому продовжуємо здiйснювати обчислення далi.

Крок 1.5: i = 4, 154*2⁴ = 1232*2 = 2464, i + 1 = 5, умову 2⁵ = 32 > 23 виконано, а тому зупиняємо подальшi обчислення.

Етап 2. Представимо число А = 23 у виглядi полiному:

1•2⁰ + 1•2¹ + 1•2² + 0•2³+ 1•2⁴,

тобто сформуємо його як суму чисел 1, 2, 4 i 16, якi вiдповiдають значенням ступенiв i = 0, 1, 2, 4 (2⁰ = 1, 2¹ = 2, 2² = 4, 2⁴ = 16).

Етап 3. Обчислимо добуток чисел В = 154 та А = 23 шляхом додавання значень В *2 ⁱ для тих i = 0, 1, 2, 4, якi увiйшли до визначення числа А, тобто наступних значень: 154 (i = 0); 308 (i = 1); 616 (i = 2); 2464 (i = 4).

У пiдсумку, буде отримано наступну суму, що являє собою добуток 154 на 23: 154 + 308 + 616 + 2464 = 3542.

Простаферитичний спосіб множення, назва якого походить від грецьких слiв простезис (додавання) та афайрезис (віднімання), оснований на наступнiй тотожності:

За значеннями суми та різниці співмножників A та B, на основi таблиці виду Х ² знаходять промiжнi величини C i D виду

C = (A + B)² / 4,

D = (A - B)² / 4.

Остаточно добуток формується після виконання операції віднімання:

AB = (С – D).

Розглянемо реалiзацiю алгоритму простаферитичного способу множення на прикладi знаходження добутку чисел А = 154 та В = 24.

C = (A + B)² / 4 = (154 + 24) ² / 4 = 178 ² / 4 = 31684/ 4 = 7921,

D = (A - B)² / 4 = (154 - 24)² / 4= 130 ² / 4 = 16900 / 4 = 4225,

154*24 = (С – D) =7921 – 4225 = 3696.

Давньоіндійський спосiб множення «хрест нахрест» використовує наступну властивість: при множенні двох чисел А i В, представлених у позиційній однорідній системі числення з основою р, відповідно правилам множення поліномів, цифра розряду (з вагою) рⁱ може бути отримана як сума всіх однорозрядних добутків виду

(a_ib₀ + a_i-1b₁ + … + a₁b_i-1 + a₀b_i +П_i-1),

де a_i і b_i - цифри i-х розрядів чисел А i В, відповідно, П_i-1 - перенос з розряду р^i-1 добутку.

Дійсно, якщо представити числа А i В у вигляді поліномів з основою р, то одержимо наступне:

Тоді добуток отримає вигляд

C = A * B = (a_npⁿ + a_{n- 1} p^{n- 1} + a₀p⁰) * (b_kp^k + b_{k- 1} p^{k- 1} + b₀p⁰).

Оскiльки результат С також є позиційним числом з основою p, то він може бути представлений у наступний спосiб: C = c_mp^m + c_{m- 1} p^{m- 1}+… + c₀p⁰,

де m = n + k.

Тоді будемо мати представленi нижче значення:

c₀ = a₀b₀,

c₁ = a₁b₀ + a₀b₁ +П₀,

c₂ = a₂b₀ + a₁b₁ + a₀b₂ + П₁,

…

Очевидно, що сума індексів множників однорозрядних добутків a_іb_j для цифри розряду з вагою р^к дорівнює індексу к, тобто: " i, j к=i+j.

 

Таким чином, для послідовного визначення розрядів результату множення двох чисел за допомогою давньоіндійськогоспособу множення «хрест нахрест», потрібен тільки однорозрядний суматор з основою р.

Паралельне формування розрядів результату вимагає застосування значно більшого обсягу устаткування.

Розглянемо приклад застосування давньоіндійського способу множення «хрест нахрест» до отримання добутку чисел А = 132 та В = 23.

Представимо множники А = 132 та В = 23 у виглядi полiномiв:

A = 1*10²+3*10¹+2*10⁰,

В = 2*10¹+3*10⁰.

Тоді добуток отримає наступний вигляд:

С = А*В = 6*10⁰+(9*10¹+4*10¹+(3*10²+6*10¹*10¹+0*2*10⁰*10²))+2*10³= =3*10³ +0*10²+3*10¹+6*10⁰.

Названі вище способи множення (давньоєгипетський, простаферитичний i давньоiндiйський) при р>2 застосовуються рідко.

Наприклад:

- давньоєгипетський спосіб множення застосовувався в деяких обчислювальних машинах ранніх поколінь;

- простаферитичний спосіб множення використовується в комп`ютерах iз порівняно невеликою довжиною слова, що дозволяє застосовувати постійний запам'ятовуючий пристрій (ПЗП) для збереження квадратів чисел;

- давньоiндiйський спосіб «хрест нахрест» використовується в деяких спеціалізованих комп`ютерах, якi виконують великий обсяг множень по основі р > 2, а його модифікація використовується в двійкових комп`ютерах при апаратній реалізації операції множення.