Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методология выбора наилучшего алгоритма оптимизации
Конкретную детерминированную задачу оптимизации можно решить различными алгоритмами. Отсюда возникают вопросы: · какой алгоритм выбрать? · какой алгоритм является «наилучшим»? Ответ на эти вопросы возможен только в том случае, когда определен класс функций {Ф(X)}, которому принадлежит критерий оптимальности Ф(X). Без определения этого класса ответить на поставленные вопросы невозможно – нет алгоритма, наилучшего для всех возможных функций Ф(X). Множество рассматриваемых алгоритмов оптимизации обозначим {A}. Причем, мультиверсионную систему, объединяющую несколько методов оптимизации, мы здесь будем считать за один новый метод оптимизации. Для формальной постановки задачи определения наилучшего алгоритма из множества {A} на классе функций {Ф(X)} необходимо еще ввести критерий качества алгоритма оптимизации. Обозначим этот критерий W(Ф,A), где Ф Для построения критерия качества алгоритма на всем классе функций {Ф(X)} можно воспользоваться · принципом гарантированного результата: · некоторым средним значением критерия качества алгоритма на классе функций {Ф(X)}. Если критерий качества алгоритма на классе функций {Ф(X)} тем или иным образом определен, то задача отыскания наилучшего алгоритма оптимизации на этом классе функций формально может быть записана в следующем виде: Теоретическое решение такой задачи возможно только для алгоритмов поиска минимума одномерных унимодальных функций. В более сложных случаях сравнение алгоритмов поисковой оптимизации и выбор из них наилучшего производится на основе экспериментального тестирования. В качестве критерия качества алгоритма оптимизации W(Ф,A) обычно рассматривают затраты времени на поиск. Эти затраты складываются · из затрат на испытания · из затрат на нахождение точек X r по информации о предыдущих испытаниях (можно сказать – из затрат на вычисления значений функции). Обычно, на практике, последние затраты много меньше первых, поэтому в качестве критерия качества алгоритма оптимизации A можно использовать количество испытаний
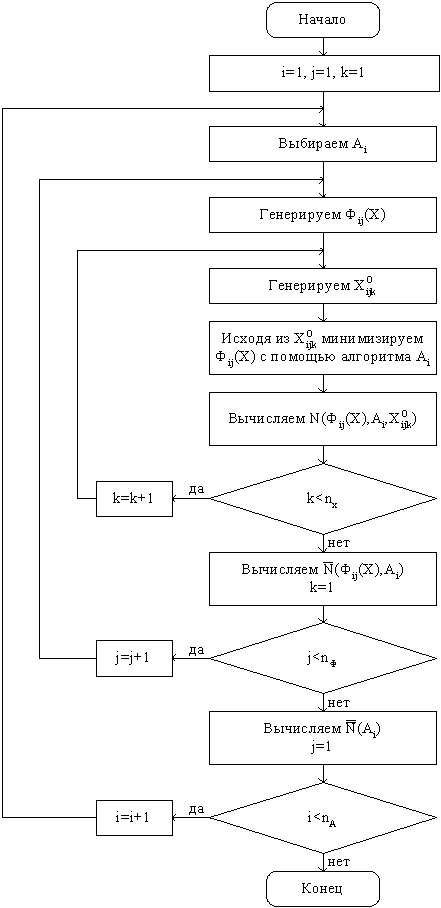
Для корректного сравнения эффективности различных алгоритмов, экспериментальное тестирование алгоритмов оптимизации необходимо выполнять при одинаковых значениях заданной точности решения ε. Поэтому будем в качестве критерия качества алгоритма оптимизации A на классе функций {Ф(X)} использовать критерий При заданной точности решения эффективность любого алгоритма поисковой оптимизации зависит от начального приближения X 0. Поэтому при экспериментальном тестировании обычно критерий Точность решения задачи оптимизации определяется используемым условием окончания поиска. При экспериментальном тестировании в качестве такого условия будем использовать одно из двух условий: Заметим, что эти условия накладывают на класс тестовых функций дополнительное требование: у этих функций априори должно быть известно положение истинного минимума Сделаем следующие предположения: · множество тестируемых алгоритмов {A} состоит из nA алгоритмов A i, · при тестировании алгоритма A i, · при тестировании алгоритма A i, В сделанных предположениях общую схему экспериментального тестирования алгоритмов оптимизации можно представить в следующем виде (см. рисунок 3.12).
Рисунок 3.12 Общая схема экспериментального тестирования алгоритмов поисковой оптимизации Классы тестовых функций
|
|||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 193; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.89.173 (0.007 с.) |
 {Ф(X)}, A
{Ф(X)}, A  ;
;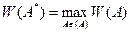 .
. , необходимых для нахождения минимума функции Ф(X) с заданной точностью ε при начальном приближении X 0.
, необходимых для нахождения минимума функции Ф(X) с заданной точностью ε при начальном приближении X 0. .
.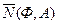 .
. или
или  , где
, где  - значение функции Ф(X) в точке истинного минимума, а
- значение функции Ф(X) в точке истинного минимума, а 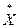 - точка истинного минимума функции Ф(X),
- точка истинного минимума функции Ф(X),  - некоторая векторная норма.
- некоторая векторная норма.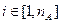 ;
; ;
;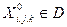 ,
, 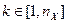 .
.