
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. Решение систем линейных уравнений методом Жордана-Гаусса
Системой линейных алгебраических уравнений называется совокупность формальных равенств вида:
где а ij, bi
Матрицы
называются соответственно матрицей системы и расширенной матрицей системы. Решением системы (1) называется упорядоченная совокупность чисел Х = (с 1, с 2,..., с n), которые при подстановке с j «x j (j = 1,..., n) обращают каждое уравнение системы (1) в верное равенство. Система, имеющая хотя бы одно решение, называется совместной, иначе – несовместной. Решить систему – означает найти все ее решения. Две системы называются эквивалентными или равносильными, если они имеют одинаковые множества решений. Аналогично, расширенные матрицы эквивалентных систем будем называть эквивалентными.
Например, системы
5х1 - 2х2 = 1, 9х1 = 9, х1 = 1 с расширенными матрицами
являются эквивалентными, так как все они имеют единственное решение Х = (1, 2). Элементарными преобразованиями матрицы называются: перестановка местами любых двух строк; умножение строки на любое, отличное от нуля число; прибавление к одной строке матрицы любой другой строки, умноженной на любое число; удаление нулевой строки. Решение системы методом Гаусса и его модификацией – методом Жордана-Гаусса основано на следующем утверждении: матрица, полученная элементарными преобразованиями расширенной матрицы системы эквивалентна исходной матрице, т.е. элементарные преобразования расширенной матрицы системы не изменяют множества решений системы. Суть обоих методов состоит в том, чтобы при помощи элементарных преобразований привести расширенную матрицу системы к наиболее простому виду, т.е. к такому виду, когда решение найти достаточно легко. Например, ясно, что систему S1 c матрицей
Переменная xj называется базисной в i – ом уравнении системы (1) если
aij = 1 и akj = 0 при k ≠ i, k = 1, 2,..., m. Другими словами, переменная xj вляется базисной в i – ом уравнении, если коэффициент при ней в этом уравнении равен 1, а в остальных уравнениях - 0, т.е. в других уравнениях этой переменной нет. Говорят, что матрица системы приведена к базисному виду (или имеет базис) если в каждом ее уравнении имеется базисная переменная. Например, матрица Справедливо следующее утверждение: При помощи элементарных преобразований расширенную матрицу любой совместной системы можно привести к базисному виду. Если матрица системы приведена к базисному виду, то переменные, не являющиеся базисными, называются свободными. Например, в матрице Решение системы, полученное после приравнивания нулю всех свободных переменных, называется базисным.
|
|||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.125.219 (0.004 с.) |
 (1)
(1)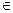 R - заданные числа, x j - неизвестные, 1 £ i £ m, 1 £ j £ n.
R - заданные числа, x j - неизвестные, 1 £ i £ m, 1 £ j £ n.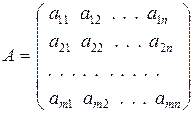 и
и 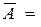
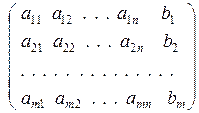

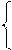
 S: 2х1 + х2 = 4 S1: 2х1 + х2 = 4 S2: х2 = 2
S: 2х1 + х2 = 4 S1: 2х1 + х2 = 4 S2: х2 = 2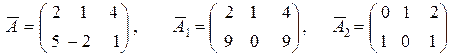
 решить легче, чем исходную систему S с матрицей
решить легче, чем исходную систему S с матрицей 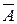 , а решение системы S2 вообще очевидно. Переход от матрицы
, а решение системы S2 вообще очевидно. Переход от матрицы 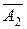 , можно поступить следующим образом: сначала вторую строку
, можно поступить следующим образом: сначала вторую строку 


