
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Положение прямых относительно плоскостей проекцийСтр 1 из 5Следующая ⇒
Ответы по начертательной геометрии.
Все точки прямой нельзя изобразить на чертеже, так как она бесконечна. Прямую можно задать (изобразить) на чертеже, например, в виде ее отрезка. Рассмотрим ортогональное проецирование отрезка АВ на плоскость П 1. Проецирующие лучи AA 1 и BB 1, проведенные из точек А и В прямой, образуют плоскость S, пересекающуюся с плоскостью проекций П 1. Линия пересечения плоскостей П 1 и S проходит через проекции A 1 и B 1 точек А и В на плоскости проекций П 1. Эта линия и является единственной прямой на плоскости П 1.
Наглядное изображение проецирования отрезка АВ на две плоскости проекций показано на рис.А, комплексный чертеж - на рис. Б. Точка принадлежит прямой, если соответствующие проекции точки расположены на соответствующих проекциях прямой.
Видимость Определение видимости геометрических фигур на плоскости проекций выполняют с использованием конкурирующих точек.
Конкурирующие точки находим в пересечении проекций прямой с проекциями треугольника ABC - это точки 1 и 2 их проекции 1` и 2` на плоскость H совпадают.
3. Задание и изображение плоскости на чертеже. Принадлежность прямой плоскости. Главные линии плоскости.
Принадлежность точки прямой
В символической форме эти выражения могут быть записаны Задача на принадлежность точки прямой может быть выражена следующим образом:
Главные линии плоскости Среди прямых линий, принадлежащих плоскости, особое значение имеют прямые, занимающие частное положение в пространстве:
1. Горизонтали h - прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций (hÎ АВС, h//P1, h2//Ох,h3//Оy)
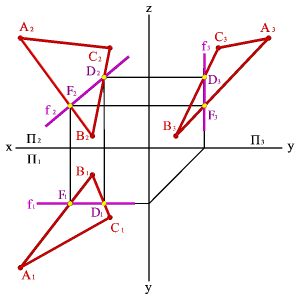
2.Фронтали f - прямые, расположенные в плоскости и параллельные фронтальной плоскости проекций (fÎ АВС, f//P2, f1// Ох, f3// Оz).
3. Профильные прямые р - прямые, которые находятся в данной плоскости и параллельны профильной плоскости проек ций (рÎ АВС, р//P3,р1^ Ох, р2^ Ох). Следует заметить, что следы плоскости можно отнести тоже к главным линиям. Горизонтальный след - это горизонталь плоскости, фронтальный - фронталь и профильный - профильная линия плоскости. 4. Прямые, принадлежащие плоскости и образующие с плоскостью проекций наибольший угол называются линиями наибольшего наклона данной плоскости к плоскости проекций. С помощью линий наибольшего наклона определяют двугранные углы между заданной плоскостью и соответствующей плоскостью проекций.
Прямые плоскости, перпендикулярные соответствующим линиям уровня являются линиями наибольшего наклона. Линия наибольшего наклона к горизонтальной плоскости проекций называется линией ската. Такое название объясняется тем, что эта линия является траекторией, по которой шарик скатывается с данной плоскости. По отношению к плоскостям П2 и П3 целесообразнее употреблять название линия наибольшего наклона.
4. Положение плоскости относительно плоскостей проекции.
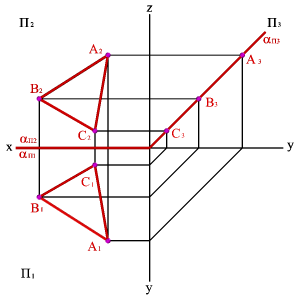
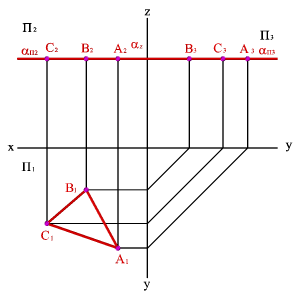
В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения. 1. Плоскость не перпендикулярная ни одной плоскости проекций называется плоскостью общего положения. Такая плоскость пересекает все плоскости проекций (имеет три следа: - горизонтальный aП1; - фронтальный aП2; - профильный aП3). 2.Плоскости, перпендикулярные плоскостям проекций – занимают частное положение в пространстве и называются проецирующими. В зависимости от того, какой плоскости проекций перпендикулярна заданная плоскость, различают:
2.1. Плоскость, перпендикулярная горизонтальной плоскости проекций (a^П1), называется горизонтально проецирующей плоскостью. Горизонтальная проекция такой плоскости представляет собой прямую линию, которая одновременно является её горизонтальным следом. Горизонтальные проекции всех точек этой плоскости совпадают с горизонтальным следом.
2.2. Плоскость, перпендикулярная фронтальной плоскости проекций (a^П2)- фронтально проецирующая плоскость. Фронтальной проекцией плоскости a является прямая линия, совпадающая со следом aП2.
2.3. Плоскость, перпендикулярная профильной плоскости (a^П3) - профильно проецирующая плоскость. Частным случаем такой плоскости является биссекторная плоскость.
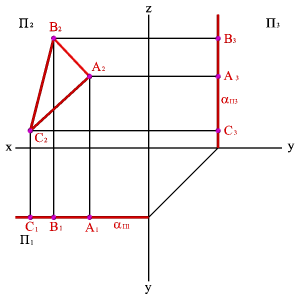
3. Плоскости, параллельные плоскостям проекций – занимают частное положение в пространстве и называются плоскостями уровня. В зависимости от того, какой плоскости параллельна исследуемая плоскость, различают:
3.1. Горизонтальная плоскость - плоскость, параллельная горизонтальной плоскости проекций (a//П1) - (a^П2,a^П3). Геометрический объект, принадлежащий этой плоскости проецируется на плоскость П1 без искажения, а на плоскости П2 и П3 в прямые - следы плоскости aП2 и aП3.
3.3. Профильная плоскость - плоскость, параллельная профильной плоскости проекций (a//П3), (a^П1, a^П2). Геометрический объект, принадлежащий этой плоскости проецируется на плоскость П 3 без искажения, а на плоскости П1 и П2 в прямые - следы плоскости aП1 и aП2.
5. Методы проецирования.
Центральное проецирование Центральный (конический или полярный) метод проецирования основан на том, что при проецировании на плоскость ряда точек (А, B, C и т.д.) все проецирующие лучи проходят через одну точку, называемую центром проецирования, или полюсом.
Метод центрального проецирования не удовлетворяет целому ряду условий, необходимых для технического чертежа, а именно: не дает однотипности изображения, полной ясности всех геометрических форм, не обладает удобоизмеримостью, не имеет простоты изображения.
Метод параллельного (косоугольного) проецирования заключается в том, что все проецирующие лучи, проходящие через точки треугольника АВС, будут параллельны между собой. Этот метод вытекает из метода центрального проецирования, при этом полюс должен быть удален на бесконечно большое расстояние от плоскости, на которую проецируется предмет.
Ортогональное проецирование Ортогональный (прямоугольный) метод проецирования – метод, когда проецирующие лучи параллельны между собой и перпендикулярны к плоскости проекций. Данный метод – частный случай параллельного проецирования.
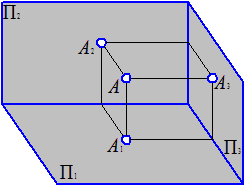
Таким образом, любая точка пространства может быть спроецирована на плоскости проекций: на горизонтальную П1, фронтальную П2 и профильную П3. Горизонтальная проекция точки обозначается А1 или А′, фронтальная А2 или А″, профильная А3 или А′″.
Классификация поверхностей. Задание поверхности на комплексном чертеже. Поверхности разделяют: o По закону образования - на закономерные и незакономерные. o По признаку развёртывания в плоскость - развёртывающиеся и неразвёртывающиеся. o По форме образующей: o По способу перемещения образующей:
Поверхности на комплексном чертеже могут быть заданы: o Проекциями направляющих и способом перемещения по ним образующих. o Семейством линий, принадлежащих поверхности - каркасный способ задания поверхности. o Очерком поверхности, т.е. линиями, ограничивающими на комплексном чертеже область существования проекций. 2. Линейчатые поверхности: Линейчатая поверхность в общем случае однозначно определяется тремя направляющими линиями, т.е. при перемещении по ним образующей. Линейчатые поверхности делятся на развёртывающиеся и неразвёртывающиеся. К развёртывающимся относятся: цилиндрические поверхности, конические поверхности, поверхности с ребром возврата (торса), призматические поверхности, пирамидальные поверхности.
Цилиндрическая поверхность.
Коническая поверхность получается при движении прямолинейной образующей l по криволинейной направляющей m, причём образующая l постоянно проходит через неподвижную точку S. Цилиндр
Пусть задан прямой цилиндр, плоскости основания которого параллельны плоскости П 1(рис.). Решим задачу. Зная фронтальные проекции точек А и В, лежащих на боковой поверхности цилиндра, построить отсутствующие проекции. Поскольку на П 1 боковая поверхность цилиндра проецируется в окружность, то А 1 и В 1 лежат, очевидно, на ней. Их положение находим по вертикальным линиям связи. Профильные проекции А 3, В 3 лежат, как известно, на горизонтальных линиях связи с фронтальными проекциями А 2 и В 2. При этом, в соответствии с правилами ортогонального проецирования, расстояние от Ф3 до профильной проекции точки равно расстоянию от Ф1 до горизонтальной проекции точки. Причем точка В 3 – невидимая, так как лежит на невидимой части боковой поверхности цилиндра. Решим следующую задачу: по заданной фронтальной проекции А2В2 линии (рис.) построим отсутствующие проекции. Горизонтальная проекция А1В1 совпадает с окружностью, так как все точки линии АВ лежат на боковой поверхности цилиндра.
Конус
Решим те же задачи построения проекций точки и линии, лежащих на поверхности конуса (рис.).
Для построение горизонтальной проекции точки, например А, необходимо через ее фронтальную проекцию провести горизонтальную линию. Тогда на П 1 эта линия 12 представляет собой дугу окружности диаметром 1222=1121. По линии связи на ней находим А 1. Аналогично, проводя дугу окружности радиусом S 131, равным расстоянию от оси конуса до точки 32 на его контуре, определяем положение на ней точки В 1. По этим проекциям находим положение А 3, В 3. По известной проекции А 2 В 2 линии на поверхности конуса построить горизонтальную и профильную. Выбрав на линии А 2 В 2 промежуточную точку 42, найдем 41 так же, как сделали это для точек А и В. Соединив точки А 1, 41, В 1, получим горизонтальную проекцию линии АВ. Для построения профильной проекции А 3 В 3 необходимо найти положение контурной точки 4, лежащей на SA. По фронтальной проекции 42, лежащей на S 2 A 2, находим профильную проекцию 43, лежащую на S 3 A 3. Теперь точки А 3, 43, В 3 можно соединить линией. При соединении точек линией всегда надо руководствоваться достаточно очевидным правилом: на каждой проекции точки, принадлежащие линии, следует соединять в одинаковой последовательности. Так, если на фронтальной проекции точка 4 является промежуточной, то она будет промежуточной и на других проекциях.
Сфера
Проекцией сферы на любую плоскость проекций является окружность. Рассмотрим построение проекций точек на поверхности сферы (рис. 4.6). Задача состоит в том, чтобы по известным проекциям построить отсутствующие. Для упрощения решения необходимо все характерные точки сферы обозначить. Точки, лежащие на экваторе, обозначим через А, В, С, D; точки, лежащие на главном меридиане – А, Е, С, F. Очевидно, что точки А и С принадлежат одновременно и экватору, и главному меридиану.
При построении проекций следует иметь ввиду, что любая параллель на П 2 проецируется в горизонтальную прямую, а на П 1 в окружность.
Рассмотрим другую точку N, проекция которой N 2 на П 2 является невидимой. Аналогично предыдущему построим N 1, лежащую на дуге окружности радиусом F 121. Так как N 2 - невидимая, то N 1 лежит выше оси Ф1. А поскольку точка N находится на поверхности нижнего полушария, что видно из положения N 2, то N 1 - невидимая. Профильная проекция N 3 строится по известному правилу взаимосвязи проекций. При этом, так как N 1 лежит выше оси Ф1, то N 3 - левее Ф3. Поскольку точка N лежит в правом полушарии, то на П 3 она невидимая, так как на П 3 все правое полушарие закрыто от нас левым и является невидимым. Видимость и невидимость полушарий, а следовательно, и точек, лежащих на них, можно легко определить, рассматривая с разных точек зрения обыкновенный резиновый мячик, нарисовав на нем экватор и два меридиана, расположенных в плоскостях, перпендикулярных друг другу. Построим горизонтальную и профильную проекции линии МN, если известна ее фронтальная проекция М 2 N 2, состоящую из прямолинейных отрезков М 232 и 32 N 2. Очевидно, что точка 31 лежит на А 1 Е 1, так как 32 - на А 2 Е 2. При этом прямая МN проходит через экватор (точка 42). Следовательно, на П 1 – через точку 41. А участок 4131 – невидимый, поскольку, как видно по его фронтальной проекции 4232, он лежит в нижнем полушарии, т.е. ниже экватора. Для построения проекций участка 3 N выберем промежуточную точку 52. Тогда точка 51 лежит на дуге окружности радиуса 5262. Соединив точки 31, 51, N 1, получим искомую линию М 1413151 N 1. Построим профильную проекцию М 3 N 3, которая проходит через те же промежуточные точки. Так как М 232 – вертикальная прямая, то на П 3 она представляет собой дугу М 333 окружности радиуса 4232=А333. Точка 53 – контурная для профильной проекции сферы. Значит, остается соединить точки 33, 53, N3 кривой линией. При этом участок 53 N 3 – невидимый. Если в нашу задачу входит более точное построение проекций линии MN, тогда на всех участках, где ее проекции не являются отрезками прямой или окружности, необходимо выбрать несколько промежуточных точек.
Следы прямой
Следами прямой называют точки её пересечения с плоскостями проекций. В зависимости от того, какую плоскость проекций пересекает прямая в данной точке, различают горизонтальный, фронтальный и профильный след. Прямые, занимающие общее положение, пересекают три плоскости проекций, линии уровня – две, а проецирующие прямые – одну. Алгоритм построения следов на эпюре Найдем следы прямой a, заданной отрезком AB. Как видно на рисунке ниже, AB занимает общее положение, поэтому для решения задачи необходимо построить проекции трех точек.
1. 2. Фронтальный след Fa. Продлим горизонтальную проекцию a' до пересечения с осью X в точке Fa'. Полученная точка – горизонтальная проекция фронтального следа*. По линии связи на прямой a'' найдем точку Fa". Она является фронтальной проекцией фронтального следа и совпадает с т. Fa. 3. Профильный след Wa строится аналогично. Для нахождения двух его проекций, Wa'' и Wa', необходимо продлить a'' и a' до пересечения с осью Z.
На следующем рисунке показано построение следов горизонтали b, заданной отрезком CD. Как и другие линии уровня, горизонталь пересекает только две плоскости проекций.
Несмотря на то, что рассмотренный нами алгоритм универсален, лучше понять смысл геометрических построений позволяет наглядное изображение прямой в пространстве. Примечание * Фронтальный след прямой по определению является точкой, которая лежит во фронтальной плоскости. Её координата Y равна нулю. Из этого следует, что горизонтальная проекция F' фронтального следа находится на оси X. Следы плоскости
Оси координат пл. α пересекает в точках Xα, Yα и Zα. Они называются точками схода следов. При этом Xα = h0α ∩ f0α, Yα = h0α ∩ p0α, Zα = f0α ∩ p0α. Здесь знак ∩ означает пересечение. На комплексном чертеже плоскость можно задать проекциями двух её следов. Это обеспечивает наглядность изображения и удобство при выполнении ряда построений. Стоит отметить, что угол, образованный следами плоскости на комплексном чертеже, не равен углу между ними в пространстве. Ответы по начертательной геометрии.
Все точки прямой нельзя изобразить на чертеже, так как она бесконечна. Прямую можно задать (изобразить) на чертеже, например, в виде ее отрезка. Рассмотрим ортогональное проецирование отрезка АВ на плоскость П 1. Проецирующие лучи AA 1 и BB 1, проведенные из точек А и В прямой, образуют плоскость S, пересекающуюся с плоскостью проекций П 1. Линия пересечения плоскостей П 1 и S проходит через проекции A 1 и B 1 точек А и В на плоскости проекций П 1. Эта линия и является единственной прямой на плоскости П 1.
Наглядное изображение проецирования отрезка АВ на две плоскости проекций показано на рис.А, комплексный чертеж - на рис. Б. Точка принадлежит прямой, если соответствующие проекции точки расположены на соответствующих проекциях прямой.
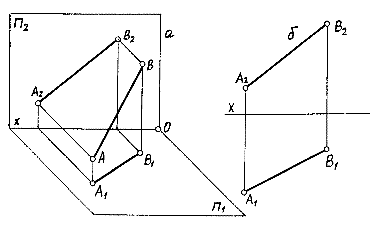
Положение прямых относительно плоскостей проекций Прямые по их положению относительно плоскостей проекций делят на прямые общего и частного положений: 1) Прямая общего положения 2) Прямые частного положения
Прямые уровня, параллельные двум плоскостям проекций, будут перпендикулярны третьей плоскости проекций. Такие прямые называют проецирующими. Различают три основные проецирующие прямые: горизонтально, фронтально и профильно проецирующие прямые.
прямой (рис. Д) называют прямой (рис. Г) называют прямую, перпендикулярную прямую, перпендикулярную плоскости П 2. Любой отрезок плоскости П 1. Любой отрезок этой прямой проецируется плоскость П 2 без искажения, на плоскость П 1 без искажения, а на плоскость П 1– в а на плоскость П 2 - в точку. точку.
2. Принадлежность точки прямой. Взаимное положение прямых. Конкурирующие точки. Видимость.
В символической форме эти выражения могут быть записаны Задача на принадлежность точки прямой может быть выражена следующим образом:
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 850; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.201.209 (0.112 с.) |
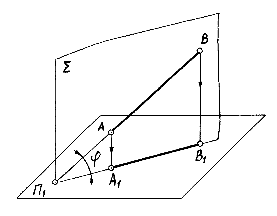
 Между длинами отрезка АВ и его проекции A 1 B 1 имеется зависимость A 1 B 1 = АВ × cos j, где j - угол между отрезком и плоскостью проекций. При (j = 00 отрезок проецируется в натуральную величину (½ A 1 B 1 ½ = ½ AB ½). При j = 900 отрезок проецируется в точку. В остальных случаях длина проекции отрезка меньше длины самого отрезка.
Между длинами отрезка АВ и его проекции A 1 B 1 имеется зависимость A 1 B 1 = АВ × cos j, где j - угол между отрезком и плоскостью проекций. При (j = 00 отрезок проецируется в натуральную величину (½ A 1 B 1 ½ = ½ AB ½). При j = 900 отрезок проецируется в точку. В остальных случаях длина проекции отрезка меньше длины самого отрезка.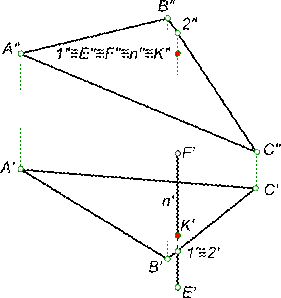
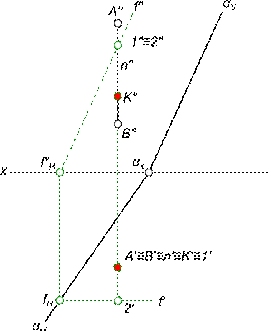 Конкурирующие точки находим в пересечении проекций прямой с проекциями плоскости α - для этого проводим в плоскости произвольную прямую f, чтобы имело место пересечение фронтальных проекций заданной прямой n и прямой f. Это точки 1 и 2 их проекции 1" и 2" на плоскость V совпадают.
Конкурирующие точки находим в пересечении проекций прямой с проекциями плоскости α - для этого проводим в плоскости произвольную прямую f, чтобы имело место пересечение фронтальных проекций заданной прямой n и прямой f. Это точки 1 и 2 их проекции 1" и 2" на плоскость V совпадают.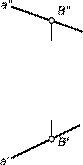 Принадлежность точки прямой на комплексном чертеже определяется согласно аксиоме инцидентности, которая устанавливает зависимости и отношения принадлежности между данными элементами евклидова пространства, которая гласит: - если точка B принадлежит прямой a, то проекции точки B` и B" принадлежат одноименным проекциям прямой a` и a" соответственно.
Принадлежность точки прямой на комплексном чертеже определяется согласно аксиоме инцидентности, которая устанавливает зависимости и отношения принадлежности между данными элементами евклидова пространства, которая гласит: - если точка B принадлежит прямой a, то проекции точки B` и B" принадлежат одноименным проекциям прямой a` и a" соответственно.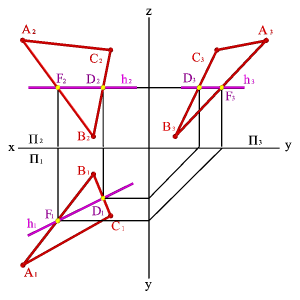
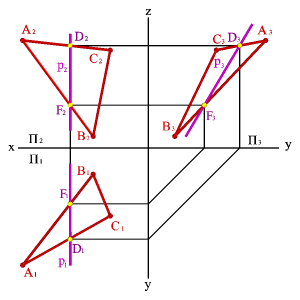
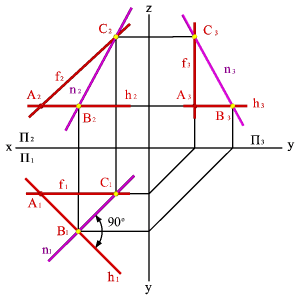 Линия ската и её горизонтальная проекция образуют линейный угол j, которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций. Горизонтальная проекция линии ската плоскости общего положения перпендикулярна горизонтальной проекции горизонталь этой плоскости. Фронтальная и профильная проекции ската строятся по её принадлежности плоскости.
Линия ската и её горизонтальная проекция образуют линейный угол j, которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций. Горизонтальная проекция линии ската плоскости общего положения перпендикулярна горизонтальной проекции горизонталь этой плоскости. Фронтальная и профильная проекции ската строятся по её принадлежности плоскости.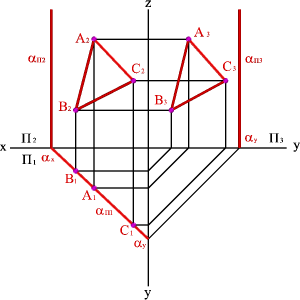
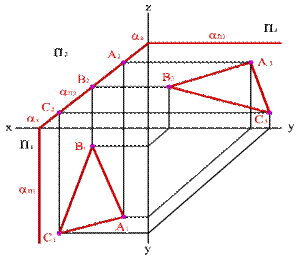
 3.2. Фронтальная плоскость - плоскость, параллельная фронтальной плоскости проекций (a//П2), (a^П1, a^П3). Геометрический объект, принадлежащий этой плоскости проецируется на плоскость П2 без искажения, а на плоскости П1 и П3 в прямы е - следы плоскости aП1 и aП3.
3.2. Фронтальная плоскость - плоскость, параллельная фронтальной плоскости проекций (a//П2), (a^П1, a^П3). Геометрический объект, принадлежащий этой плоскости проецируется на плоскость П2 без искажения, а на плоскости П1 и П3 в прямы е - следы плоскости aП1 и aП3.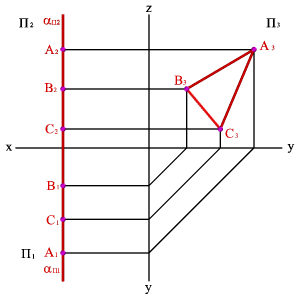
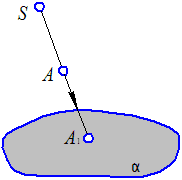 Метод проецирования заключается в том, что любая из точек множества точек пространства может быть спроецирована с помощью проецирующих лучей на любую поверхность. Для этого представим некоторую заданную поверхность (рис.1) и точку А в пространстве. При проведении луча S через точку А в направлении поверхности последний пересечет ее в точке А1. Точку А называют проецируемой точкой. Плоскость α, на которой получают проекцию, называют плоскость проекций. Точка пересечения луча с плоскостью называется проекцией точки А. Прямая АА1 (луч), называется проецирующи м лучом.
Метод проецирования заключается в том, что любая из точек множества точек пространства может быть спроецирована с помощью проецирующих лучей на любую поверхность. Для этого представим некоторую заданную поверхность (рис.1) и точку А в пространстве. При проведении луча S через точку А в направлении поверхности последний пересечет ее в точке А1. Точку А называют проецируемой точкой. Плоскость α, на которой получают проекцию, называют плоскость проекций. Точка пересечения луча с плоскостью называется проекцией точки А. Прямая АА1 (луч), называется проецирующи м лучом.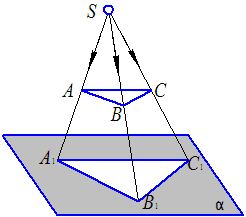 Представим в пространстве треугольник АВС и проецирующие лучи, проходящие через данный полюс S и через точки АВС треугольника, проведенные до пересечения с плоскостью α. Треугольник А1B1C1 будет центральной проекцией треугольника АВС.
Представим в пространстве треугольник АВС и проецирующие лучи, проходящие через данный полюс S и через точки АВС треугольника, проведенные до пересечения с плоскостью α. Треугольник А1B1C1 будет центральной проекцией треугольника АВС.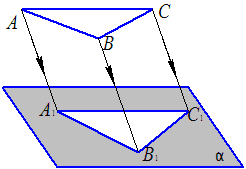 Параллельное проецирование
Параллельное проецирование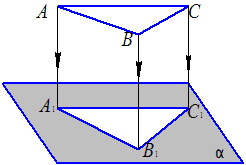
 Цилиндрическая поверхность образуется перемещением прямолинейной образующей l по криволинейной направляющей m, причём образующая l остаётся постоянно параллельной заданной направляющей S.
Цилиндрическая поверхность образуется перемещением прямолинейной образующей l по криволинейной направляющей m, причём образующая l остаётся постоянно параллельной заданной направляющей S. 2.2 Коническая поверхность.
2.2 Коническая поверхность. При построении профильной проекции А3В3 следует иметь в виду, что линия АВ пересекает прямую СD, которая на П3 является контуром С3D3цилиндра. Поэтому сначала следует определить положение контурной точки 13, а затем соединить точки А3 и В3 линией, которая в отличии от А212В2не является прямой. В связи с этим для построения необходимо на А212В2 выбрать несколько промежуточных точек (22, 32 и т.д.) и построить их профильные проекции (23, 33 и т.д.), руководствуясь вышеуказанным правилом взаимосвязи горизонтальной и профильной проекций. Чем большее количество промежуточных точек выбираем, тем более точными будут построения.
При построении профильной проекции А3В3 следует иметь в виду, что линия АВ пересекает прямую СD, которая на П3 является контуром С3D3цилиндра. Поэтому сначала следует определить положение контурной точки 13, а затем соединить точки А3 и В3 линией, которая в отличии от А212В2не является прямой. В связи с этим для построения необходимо на А212В2 выбрать несколько промежуточных точек (22, 32 и т.д.) и построить их профильные проекции (23, 33 и т.д.), руководствуясь вышеуказанным правилом взаимосвязи горизонтальной и профильной проекций. Чем большее количество промежуточных точек выбираем, тем более точными будут построения. Построим отсутствующие проекции точек А и В, расположенных на поверхности прямого кругового конуса, если известно положение А 2 и В 2.
Построим отсутствующие проекции точек А и В, расположенных на поверхности прямого кругового конуса, если известно положение А 2 и В 2. Пусть задана фронтальная проекция точки М. Проведем через нее параллель. Тогда на П 2 получим горизонтальную прямую, проходящую через точку М 2. А на П 1 – дугу окрудности радиусом F 111, равным расстоянию от вертикальной оси до токи 12. Ясно, что точка М 1 лежит на этой окружности. По двум проекциям М 1 и М 2, используя правило взаимосвязи проекций, построим М 3.
Пусть задана фронтальная проекция точки М. Проведем через нее параллель. Тогда на П 2 получим горизонтальную прямую, проходящую через точку М 2. А на П 1 – дугу окрудности радиусом F 111, равным расстоянию от вертикальной оси до токи 12. Ясно, что точка М 1 лежит на этой окружности. По двум проекциям М 1 и М 2, используя правило взаимосвязи проекций, построим М 3. Горизонтальный след Ha. Продлим фронтальную проекцию прямой a до пересечения с осью X в точке Ha''. Полученная точка – фронтальная проекция горизонтального следа. По линии связи на a' найдем точку Ha'. Она является горизонтальной проекцией горизонтального следа и совпадает с т. Ha.
Горизонтальный след Ha. Продлим фронтальную проекцию прямой a до пересечения с осью X в точке Ha''. Полученная точка – фронтальная проекция горизонтального следа. По линии связи на a' найдем точку Ha'. Она является горизонтальной проекцией горизонтального следа и совпадает с т. Ha.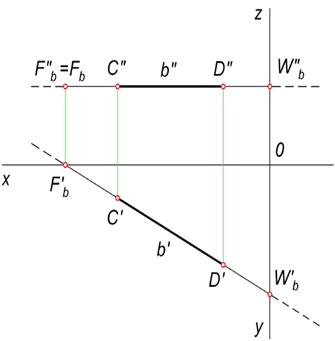
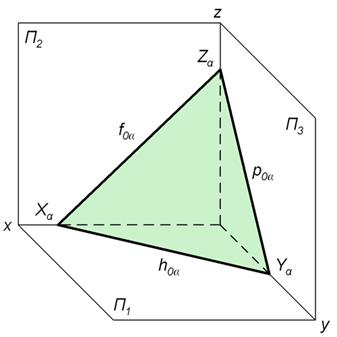 На рисунке показана плоскость общего положения α. Она пересекает плоскости проекций П1, П2, П3 по прямым h0α, f0α и p0α. Эти прямые называются горизонтальным, фронтальным и профильным следом плоскости α.
На рисунке показана плоскость общего положения α. Она пересекает плоскости проекций П1, П2, П3 по прямым h0α, f0α и p0α. Эти прямые называются горизонтальным, фронтальным и профильным следом плоскости α.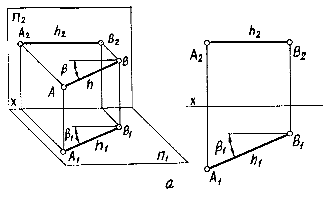 Горизонталью называют любую линию, параллельную горизонтальной плоскости проекций (рис.2.З-а). Фронтальная проекция горизонтали всегда перпендикулярна линиям связи. Любой отрезок горизонтали на горизонтальную плоскость проекций проецируется в истинную величину. В истинную величину проецируется на эту плоскость и угол наклона горизонтали (прямой) к фронтальной плоскости проекций. В качестве примера на рис.2.З-а дано наглядное изображение и комплексный чертеж горизонтали h, наклоненной к плоскости П 2 под углом b.
Горизонталью называют любую линию, параллельную горизонтальной плоскости проекций (рис.2.З-а). Фронтальная проекция горизонтали всегда перпендикулярна линиям связи. Любой отрезок горизонтали на горизонтальную плоскость проекций проецируется в истинную величину. В истинную величину проецируется на эту плоскость и угол наклона горизонтали (прямой) к фронтальной плоскости проекций. В качестве примера на рис.2.З-а дано наглядное изображение и комплексный чертеж горизонтали h, наклоненной к плоскости П 2 под углом b. 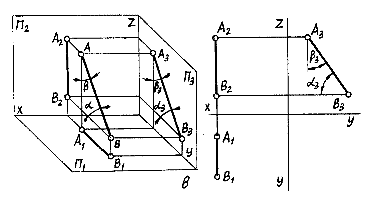 Фронталью называют линию, параллельную фронтальной плоскости проекций (рис.2.3-б). Горизонтальная проекция фронтали всегда перпендикулярна линиям связи. Любой отрезок фронтали на фронтальную плоскость проекций проецируется в истинную величину. В истинную величину проецируется на эту плоскость и угол наклона фронтали (прямой) к горизонтальной плоскости проекций (угол a).
Фронталью называют линию, параллельную фронтальной плоскости проекций (рис.2.3-б). Горизонтальная проекция фронтали всегда перпендикулярна линиям связи. Любой отрезок фронтали на фронтальную плоскость проекций проецируется в истинную величину. В истинную величину проецируется на эту плоскость и угол наклона фронтали (прямой) к горизонтальной плоскости проекций (угол a).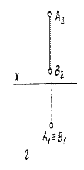
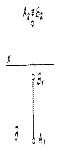 Фронтально проецирующей Горизонтально проецирующей
Фронтально проецирующей Горизонтально проецирующей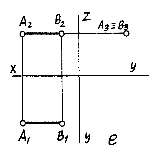 Профильно проецирующей прямой (рис.Е) называют прямую, перпендикулярную плоскости П 3, т.е. прямую, параллельную плоскостям проекций П 1 и П 2. Любой отрезок этой прямой проецируется на плоскости П 1 и П 2 без искажения, а на плоскость П 3 - в точку.
Профильно проецирующей прямой (рис.Е) называют прямую, перпендикулярную плоскости П 3, т.е. прямую, параллельную плоскостям проекций П 1 и П 2. Любой отрезок этой прямой проецируется на плоскости П 1 и П 2 без искажения, а на плоскость П 3 - в точку. Принадлежность точки прямой на комплексном чертеже определяется согласно аксиоме инцидентности, которая устанавливает зависимости и отношения принадлежности между данными элементами евклидова пространства, которая гласит: - если точка B принадлежит прямой a, то проекции точки B` и B" принадлежат одноименным проекциям прямой a` и a" соответственно.
Принадлежность точки прямой на комплексном чертеже определяется согласно аксиоме инцидентности, которая устанавливает зависимости и отношения принадлежности между данными элементами евклидова пространства, которая гласит: - если точка B принадлежит прямой a, то проекции точки B` и B" принадлежат одноименным проекциям прямой a` и a" соответственно.


