Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графическое решение задач теории игр.
Пример. Найти решение игры вида (2´n), заданной платежной матрицей:
Решение:
Игра не имеет седловой точки. Ниже представлены ожидаемые выигрыши первого игрока, соответствующие чистым стратегиям второго игрока. Чистые стратегии Ожидаемые выигрыши второго игрока первого игрока 1 2 3 4 На оси Х1 разместим точки х 1 = 0 и х 1 = 1, через которые проводим перпендикулярные оси Х1 (рис. 12.1). Подставляя х 1 = 0 и х 1 = 1 в выражение – 2 х 1 + 4, находим значения 4 и 2, которые откладываем на соответствующих перпендикулярных прямых. Соединив эти точки, получим прямую – 2 х 1 + 4. Рисунок 12.1
Аналогично строим остальные три прямые. Оптимальная стратегия первого игрока определится как максимальная точка, на нижней огибающей. В рассматриваемом случае это точка пересечения прямых, соответствующих выигрышу первого игрока при использовании вторым игроком третьей и четвертой стратегий, т.е. прямых: х 1 + 2 = – 7 х 1 + 6, х 1 = ½, х 2 = 1 – х 1 = ½. Цена игры определяется подстановкой переменной х 1 в уравнение любой из прямых, проходящих через максиминную точку: v = х 1 + 2 = ½ +2 = 2½ или v = – 7 х 1 + 6 = – 7×½ + 6 =2½. Оптимальная стратегия первого игрока Найдем оптимальную стратегию второго игрока. Из рисунка 13.1 следует, что оптимальная стратегия первого игрока определяется как точка пересечения прямых, соответствующих выигрышу первого игрока при использовании вторым игроком третьей и четвертой стратегий, поэтому у 1 = у 2 = 0, а у 4 = 1 – у 3 Чистые стратегии Ожидаемые проигрыши первого игрока второго игрока 1 2 Оптимальная стратегия второго игрока определится как точка пересечения прямых: 4 y 3 – 1 = – 4 y 3 + 6, y 3 = 7/8, y 4 = 1 – y 3 = 1 – 7/8 = 1/8 (рис.12.2). Рисунок 12.2 Цена игры v = 4 y 3 – 1 = 4×7/8 – 1 = 5/2 = 2½ или v = – 4 y 3 + 6 = – 4×7/8 + 6 = 5/2 = 2½. Оптимальная стратегия второго игрока:
Рассмотрим решение варианта 0.
Определим нижнюю цену игры – α. Нижняя цена игры α — это максимальный выигрыш, который мы можем гарантировать себе, в игре против разумного противника, если на протяжении всей игры будем использовать одну и только одну стратегию (такая стратегия называется "чистой"). Найдем в каждой строке платежной матрицы минимальный элемент и запишем его в дополнительный столбец
Затем найдем максимальный элемент дополнительного столбца (отмечен звездочкой), это и будет нижняя цена игры.
В нашем случае нижняя цена игры равна: α = 1, и для того чтобы гарантировать себе выигрыш не хуже чем 1 мы должны придерживаться стратегии A4 Определим верхнюю цену игры - β Верхняя цена игры β — это минимальный проигрыш, который может гарантировать себе игрок "В", в игре против разумного противника, если на протяжении всей игры он будет использовать одну и только одну стратегию. Найдем в каждом столбце платежной матрицы максимальный элемент и запишем его в дополнительную строку снизу Затем найдем минимальный элемент дополнительной строки (отмечен плюсом), это и будет верхняя цена игры.
В нашем случае верхняя цена игры равна: β = 1, и для того чтобы гарантировать себе проигрыш не хуже чем 1 противник (игрок "B") должен придерживаться стратегии B2 Сравним нижнюю и верхнюю цены игры, в данной задаче они совпадают, т.е. α = β = 1. Это значит, что игра имеет решение в так называемых "чистых", минимаксных стратегиях. Это как раз те стратегии для игроков "A" и "B" которые были найдены выше, при поиске нижней и верхней цен игры. То есть, в нашем случае для игрока "A" оптимальной будет стратегия A4, а для игрока "В" - B2. Нетрудно заметить, что элемент платежной матрицы расположенный на пересечении чистых оптимальных стратегий (строка 4, столбец 2) является одновременно минимальным в строке и максимальным в столбце. Такие элементы называются седловыми точками, именно их наличие и определяет существование решения игры в чистых стратегиях, а его значение (в нашем случае 1) совпадает с чистой ценой игры или просто ценой игры - v. Пара оптимальных стратегий, в играх имеющих седловую точку, всегда проходит через последнюю.
Ответ: Нижняя цена игры, верхняя цена игры и чистая цена игры: α = β = v = 1; Пара оптимальных стратегий: A4B2.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 182; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.197.123 (0.006 с.) |
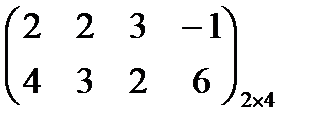 .
.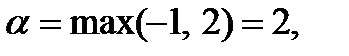
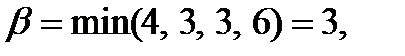
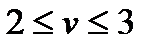 .
.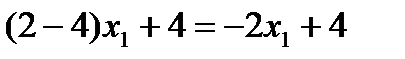
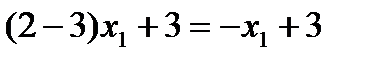
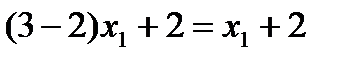

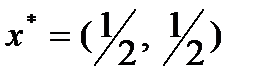 , при этом цена игры v = 2½.
, при этом цена игры v = 2½.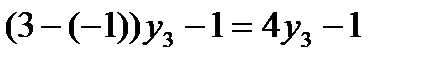
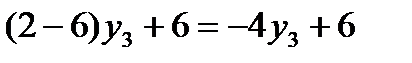
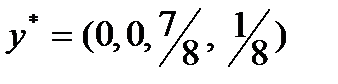 при цене игры v = 2½.
при цене игры v = 2½.