
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Табличный процессор Excel в научных исследованиях
Информация НИ достаточно часто представляется в табличной форме. Обработка такой информации эффективно выполняется с использованием табличных процессоров (ТбП) или ЭТ. Электронные таблицы применяются на всех этапах выполнения НИ, но наиболее целесообразно их использование при выполнении математических расчетов, математическом моделировании, численном эксперименте и отработке данных. Выполнение математических расчетов в ЭТ основано на возможности связывания числовых значений клеток с помощью математических операторов и встроенных функций. ТбП Excel предоставляет возможность работы с математическими, статистическими, логическими, информационными и др. категориям функции. Выбор необходимой функции выполняется с помощью Мастера функций командой Вставка\Функция или ПГ fx. При этом происходит помещение функции в “активную клетку”. В части расчетов Excel позволяет выполнять: 1. Реализацию численных методов решения дифуравнений, алгебраических уравнений и их систем. 2. Обработку векторных и матричных массивов информации. 3. Оптимизационные расчеты, включая методы математического программирования (линейное и т.д.). 4. Операции с комплексными числами. При этом расчеты сводятся к вычислению промежуточных результатов в соответствующих колонках таблиц. Моделирование и численный эксперимент в ЭТ основаны на возможности автоматического пересчета результатов и их связанном графическом отображении. Для наиболее простых случаев используется анализ по способу “ что-если ”, когда поочередно меняются значения переменных функций f=f(x, y, z,p, m...). Вариантом названного анализа является метод подбора параметра. Требуемые значения функции при этом находятся за счет варьирования переменными, от которых она зависит. Метод реализуется командой Сервис\Подбор параметра через соответствующее диалоговое окно. При этом может быть выполнено несколько операций с заданием величины числа. Эта операция. может быть реализована графически с выделением отображения переменной (Ctrl+ЩЛ) и его изменением БМ. Более сложный анализ для нахождения рационального численного решения при большем числе условий и ограничений выполняется методом поиск решения. Эта задача решается диалогом в пункте Сервис\Поиск решения. (Режим должен быть предварительно включен пунктом Сервис\Дополнения).
При обработке данных, полученных по результатам НИ Excel может быть использован для: 1. Расчета среднеарифметического и среднеквадратного отклонения наборов данных при выявлении грубых ошибок измерений. Здесь применяются функции СРЗНАЧ, КВАДРОТКЛ и т.п. 2. Статистического анализа данных. При этом может быть выполнено: - определение минимального (максимального) значения (функции МИНИ, МАКС) ряда данных, стандартное отклонение (СТАНДОТКЛОН); - корреляционный, дисперсионный анализы, анализ Фурье и т.п. через команду Сервис\Анализ данных, включаемую через диалог Сервис\Дополнения. 3. Графического отображения результатов измерений с использованием прямоугольных и логарифмических шкал осей. Последние могут быть установлены через диалоговое окно “Форматирование оси”, открываемоедвойным ЩЛ по соответствующей оси. Для удобства представления результатов на график. может быть нанесена сетка - пункт Вставка/Сетка и включены планки погрешностей - пункт Вставка/Планки погрешностей. 4.Определения коэффициентов эмпирических линейных зависимостей (функция ТЕНДЕНЦИЯ), построение регрессионных зависимостей с различными видами аппроксимации. Эта операция выполняется после выделения необходимых точек диаграммы и использования диалога Диаграмма/Добавить линию тренда, где могут быть выбраны линейное, степенное и другие виды приближений. Примеры построения математических моделей: динамика популяций, уравнения Вольтерра-Лотка, уравнения Вольтерра-Лотка с логистической поправкой, модель Холлинга-Тэннера, выравнивание цен
Дифференциальные уравнения широко используются для моделирования реальных систем, зависящих от времени, в частности, для описания и исследования экономических биологических, социальных систем.
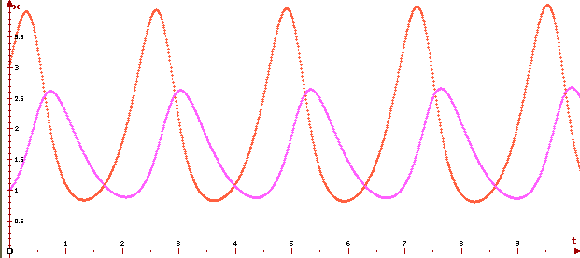
Динамика популяций. Уравнения Вольтерра-Лотка В динамике популяций есть много примеров, когда изменение численности популяций во времени носит колебательный характер. Одним из самых известных примеров описания динамики взаимодействующих популяций являются уравнения Вольтерра—Лотка. Рассмотрим модель взаимодействия хищников и их добычи, когда между особями одного вида нет соперничества.
Видно, что процесс имеет колебательный характер. При заданном начальном соотношении числа особей обоих видов 3: 1, обе популяции сначала растут. Когда число хищников достигает величины b =2.5, популяция жертв не успевает восстанавливаться и число жертв начинает убывать. Уменьшение количества пищи через некоторое время начинает сказываться на популяции хищников и когда число жертв достигает величины x 1 =c/d =2 (в этой точке x 2'=0), число хищников тоже начинает сокращаться вместе с сокращением числа жертв. Сокращение популяций происходит до тех пор, пока число хищников не достигнет величины x 2 =a/b =1.6 (в этой точке x 1'=0).С этого момента начинает расти популяция жертв, через некоторое время пищи становится достаточно, чтобы обеспечить прирост хищников, обе популяции растут, и... процесс повторяется снова и снова. На графике четко виден периодический характер процесса. Количество жертв и хищников колеблется возле величин x 1=2, x 2=1.6 соответственно (дробные числа здесь не означают “половину волка”, величины могут измеряться в сотнях, тысячах и т.п.). Периодичность процесса явственно видна на фазовой плоскости — фазовая кривая (x 1(t), x 2(t)) — замкнутая линия. Самая левая точка, этой кривой, - это точка, в которой число жертв достигает наименьшего значения. Самая правая точка x 1=4, x 2=1.6, — точка пика популяции жертв. Между этими точками количество хищников сначала убывает, до нижней точки фазовой кривой, x 1=2, где достигает наименьшего значения, а затем растет до верхней точки фазовой кривой (x 1=2, x 2=2.5). Фазовая кривая охватывает точку x 1=2, x 2=1.6. Рассмотренная модель может описывать поведение конкурирующих фирм, рост народонаселения, численность воюющих армий, изменение экологической обстановки, развитие науки и т.п.
ПРИМЕР 1. Динамика популяций.
Уравнения Вольтерра-Лотка с логистической поправкой Рассмотрим модель конкурирующих видов с “логистической поправкой”:
Видно, что в этом случае стационарная точка превращается в устойчивый фокус, а решения — в затухающие колебания. При любом начальном условии состояние системы через некоторое время становится близким к стационарному и стремится к нему при Графики решений и фазовая кривая при отрицательном значении параметра a, a =-0.1, приведены ниже.
Как видно, в этом случае стационарная точка является неустойчивым фокусом и амплитуда колебаний численности видов растет. В этом случае как бы близко ни было начальное состояние к стационарному, с течением времени состояние системы будет сильно отличаться от стационарного.
ПРИМЕР 2. Модель "хищник-жертва" с логистической поправкой.
Модель Холлинга-Тэннера На примере модели Вольтерра—Лотка и модели Вольтерра—Лотка с логистической поправкой было продемонстрировано одно из важнейших качественных свойств центров — они легко разрушаются даже при самых малых изменениях правой части. Большинство моделей является идеализацией действительности; в них внимание сосредоточено на некоторых основных переменных и соотношениях между ними. Поэтому устойчивость моделей относительно малых возмущений чрезвычайно важна в приложениях. Модели, не чувствительные к малым возмущениям, называются грубыми. Модель Вольтерра—Лотка неустойчива относительно возмущений, поскольку ее стационарное состояние — центр. Существует другой вид моделей, в которых возникают незатухающие колебания, — это модели, имеющие на фазовых портретах предельные циклы. Такая модель существует для системы конкурирующих видов — это модель Холлинга—Тэннера. · скорости размножения в отсутствие хищников — r x 1; · влиянию межвидовой конкуренции за пищу при ограниченных ресурсах (для случая конкурирующих производителей это влияние ограниченных сырьевых ресурсов) —
· влиянию хищников, в предположении, что хищник перестает убивать, когда насыщается — Скорость роста популяции хищников x '2 строится так же, как в модели Вольтерра—Лотка, в предположении, что жертвы встречаются редко. Если для поддержания жизни одного хищника нужно J жертв, то популяция из x 1 жертв сможет обеспечить пищей x 1/ J хищников. Модель роста популяции хищников, в которой их число не может превысить эту критическую величину, имеет вид
ПРИМЕР 3. Модель Холлинга-Тэннера.
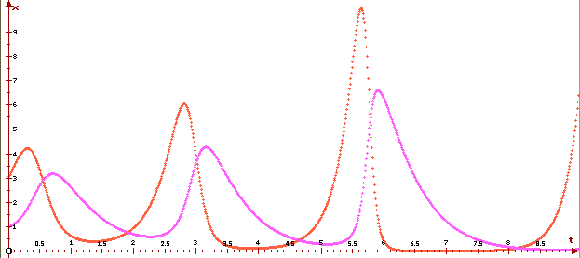
Выравнивание цен Модель выравнивания цен по уровню актива интересна тем, что в ней можно наблюдать гармонические колебания решений возле стационарного состояния. Предположим, что изменение уровня актива q пропорционально разности между предложением s и спросом d, т.е. q '= k (s - d), k > 0. Предположим далее, что изменение цены p пропорционально отклонению актива q от некоторого фиксированного уровня q 0 так, что p '=- m (q - q 0), m > 0. Таким образом, модель выравнивания цен по уровню актива имеет вид Ниже приведены график решения и фазовая кривая для Модель военных конфликтов Пусть численности армий двух противоборствующих сторон на некотором n-ом шаге военного конфликта равны xn и yn. На следующем шаге (через год, неделю, день) армии уменьшаются. Рассмотрим грубую схему, в которой за один шаг каждый воин армии x убивает в среднем воинов армии y, а каждый воин армии y убивает в среднем воинов армии x. Таким образом, на n-ом шаге армия x теряет · yn воинов, армия y теряет · xn воинов. Величины и характеризуют вооруженность сторон. Так мы получаем модель
Вначале численности армий x и y равны x0 и y0 соответственно. Пара (x0, y0) называется начальным условием. Совокупность точек (xn, yn) назовем траекторией конфликта. Конфликт заканчивается, когда либо xn Рассмотрим модель, в которой вооруженность армии y вдвое больше вооруженности армии x: в формулах положим
Картина траекторий этой системы указана на рис. 1. Мы видим, что существует единственная прямолинейная траектория, заканчивающаяся вничью: она «стремится» к точке (0,0), символизирующей полное взаимное истребление армий. Конфликт, начавшийся в одной из этих точек прямой, теоретически будет длиться бесконечно. Упомянутая прямая - сепаратриса (разделяющая).
Рис. 1. Траектория в модели военных конфликтов, определенной системой (1).
При любых начальных условиях под сепаратрисой конфликт завершается победой армии x; начальные условия над сепаратрисой гарантируют победу армии y. Найдем сепаратрису траекторий модели (17). Для того, чтобы точка (xn, yn) лежала на сепаратрисе, требуется, чтобы выполнялось равенство
Отсюда
Этот результат можно трактовать так: Если вооруженность армии y в n раз больше вооруженности армии x, то для достижения равновесия численность армии x должна быть в Итак, в этой модели превосходство в численности армии важнее превосходства в вооруженности. Слушателю представляется самому судить о согласованности этой модели с реальными военными конфликтами, давними и современными. Модель мобилизации Модель мобилизации описывает динамику изменения численности организации, вербующей себе сторонников: политических партий или движений, религиозных групп и т.п. Пусть к началу n -ого периода существования организации доля ее сторонников в населении равна xn. Тогда к началу (n +1)-го периода: некоторая доля неохваченного населения примкнет к организации вследствие агитации. Доля неохваченного населения равна (1-xn); доля примкнувших равна ¦ · (1- xn), где ¦ называется коэффициентом агитируемости. Величина ¦ находится в интервале от 0 до 1. некоторая доля сторонников отойдет от организации (умрет, разочаруется, будет исключена). Доля отошедших равна g · (1- xn). Число g называется коэффициентом выбытия. Величина g находится в интервале от 0 до 1. Таким образом, доля членов организации в начале (n +1)-го периода определится формулой xn+1 = xn + ¦ · (1-xn) - g · xn, или xn+1 = (1 - ¦ - g) · xn + ¦. (2) Стационарное значение x величины xn, удовлетворяющее уравнению (2), определяется формулой
Ввиду неравенств 0 < ¦ < 1, 0 < g < 1 величина коэффициента (1 - ¦ - g) в уравнении (2) находится в интервале от (-1) до 1. В этих обстоятельствах при любых начальных условиях величина xn приближается к стационарному значению с ростом n. Но если ¦ + g < 1, то xn приближается к стационарному значению монотонно; если ¦ + g > 1, то приближение идет с колебаниями. На рис. 2 показаны траектории системы вида (2) при коэффициенте агитируемости ¦, равном 0,04 и коэффициенте выбытия g, равном 0,06. Таким образом, рис. 2 иллюстрирует динамику траекторий уравнения xn+1 = 0,9 · xn + 0,04 (3) На рис. 3 показан вариант колебательного приближения величины xn к своему стационарному значению. Для удобства мы построили только одну колебательную траекторию. Здесь коэффициент агитируемости ¦ равен 0,6 и коэффициент выбытия g равен 0,9. Таким образом, рис. 3 иллюстрирует динамику одной из траекторий уравнения xn+1 = -0,5 · xn + 0,6. (4) Рисунки 2 и 3 демонстрируют устойчивость стационарной величины в модели и устойчивость модели мобилизации в целом.
Рис. 2 Модель мобилизации (3). Вариант монотонного приближения к стационарному значению.
Рис. 3. Модель мобилизации (4). Вариант колебательного приближения к стационарному значению. Экономически интерпретация модели мобилизации (уравнения (1)) может быть, например, такой: доходы xn+1 в (n + 1) -м году некоторого лица поступают из двух источников. Первый источник - величина ¦ - постоянные поступления, не зависящие от доходов прошлого года (возможно, пенсия или доходы от ценных бумаг). Наш анализ показывает, что ежегодные доходы в модели со временем приближаются к некоторой величине, не зависящей от начальных условий.
Имитационное моделирование
|
|||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 1207; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.247.31 (0.093 с.) |
 , c >0, наличие пищи компенсирует убывание, и при x1>0 имеем
, c >0, наличие пищи компенсирует убывание, и при x1>0 имеем  , d>0.
, d>0. 




 .
.

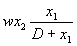
 .
. 




 0, но yn > 0 (победа армии y), либо yn
0, но yn > 0 (победа армии y), либо yn  ;
;  Получим модель
Получим модель
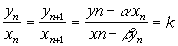 .
. .
. раз больше численности армии y.
раз больше численности армии y. .
.




