Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация корректирующих кодов.
Помехоустойчивые или корректирующие коды (рисунок 6.1) делятся на блочные и непрерывные. К блочным относятся коды, в которых каждому символу алфавита сообщений соответствует блок (кодовая комбинация) из n(i) элементов, где i – номер сообщения. Если n(i)=n, т.е. Длина блока постоянна и не зависит от номера сообщения, то код называется равномерным. Такие коды чаще применяются на практике. Если длина блока зависит от номера сообщения, то блочный код называется неравномерным. Примером неравномерного кода служит код морзе. В непрерывных кодах передаваемая информационная последовательность не разделяется на блоки, а проверочные элементы (проверочные элементы в отличие от информационных, относящихся к исходной последовательности, служат для обнаружения и исправления ошибок и формируются по определенным правилам) размещаются в определенном порядке между информационными.
Равномерные блочные коды делятся на разделимые и неразделимые. В разделимых кодах элементы разделяются на информационные и проверочные, занимающие определенные места в кодовой комбинации, во-вторых, отсутствует деление элементов кодовых комбинаций на информационные и проверочные. К последним относится код с постоянным весом, например рекомендованный международным консультативным комитетом по телефонии и телеграфии (мкктт), семиэлементный телеграфный код № 3 с весом каждой кодовой комбинации, равным трем. Примерами систематических кодов являются коды хемминга и циклические. Последние реализуются наиболее просто, что и привело к их широкому использованию в узо. Для систематического кода применяется обозначение (n,k) – код, где n – число элементов в комбинации; k – число информационных элементов. Характерной особенностью этих кодов является также и то, что информационные и проверочные элементы связаны между собой зависимостями, описываемыми линейными уравнениями. Отсюда возникает и второе название систематических кодов – линейные. Код хемминга. Рассмотрим в качестве примера построение систематического кода с кодовым расстоянием d0=3 (кода хемминга). Пусть число сообщений, которое необходимо передать, равно 16. Тогда необходимое число информационных элементов k=log2na=4. Можно выписать все 16 кодовых комбинаций, включая нулевую (0000). Это один из возможных способов задания исходного (простого) кода. Другой способ заключается в выписывании только четырех кодовых комбинаций простого кода в виде матрицы, называемой единичной:
Суммируя по модулю два в различном сочетании кодовые комбинации, входящие в единичную матрицу, можно получить 15 кодовых комбинаций, 16-я – нулевая. Кодовые комбинации, составляющие матрицу (6.1), линейно независимы. Можно было бы составить матрицу и из других кодовых комбинаций (лишь бы они были линейно независимыми). Ненулевые комбинации a1, a2, a3, a4 линейно независимые, если q1a1
Складывая строки 1 и 2 матрицы (6.2) по модулю два
Видим, что они отличаются только в двух элементах, т.е. Заданное кодовое расстояние не обеспечивается. Дополним каждую строку проверочными элементами так, чтобы d0=3. Тогда матрица примет вид
Добавляемые проверочные элементы могут быть записаны и в другом порядке. Необходимо лишь обеспечить d0=3. Матрицу (6.3) называют производящей, или порождающей, матрицей кода (6,4), содержащего семь элементов, из которых четыре информационных. Обычно матрицу обозначают буквой g с индексом, указывающим, к какому коду она относится (в нашем случае g (7,4)). Производящая матрица состоит из двух матриц - единичной (размерности k∙k) и с (r,k), содержащей r столбцов и k строк. Суммируя в различном сочетании строки матрицы (6.3), получаем все (кроме нулевой) комбинации корректирующего кода с d0=3.
Обозначим элементы комбинации полученного семиэлементного кода a1, a2, a3, a4, a5, a6, a7, из которых a1, a2, a3, a4 – информационные и a5, a6, a7 – проверочные. Последние могут быть получены путем суммирования по модулю два определенных информационных элементов. Разумеется, правило формирования проверочного элемента ai для любой кодовой комбинации одинаково. Найдем правило формирования элемента a5, пользуясь матрицей (6.3). Из первой строки следует, что в суммировании должен обязательно участвовать элемент a1 (только в этом случае a5=1), из второй - что элемент a3 в суммировании не должен участвовать, а из четвертой - что элемент a4 должен участвовать в суммировании. Итак,
уравнения для a6 и a7 по аналогии записываются в виде:
алгоритм формирования проверочных элементов a5, a6, a7 может быть задан матрицей, называемой проверочной. Эта матрица содержит r строк и n столбцов. Применительно к сформированному нами коду (6,4) она имеет вид:
единицы, расположенные на местах, соответствующих информационным элементам матрицы н (6,4), указывают на то, какие информационные элементы должны участвовать в формировании проверочного элемента. Единица на месте, соответствующем проверочному элементу, указывает, какой проверочный элемент получается при суммировании по модулю два информационных элементов. Так, из первой строки следует равенство
Процедура обнаружения ошибок основана на использовании проверок (12.4)-(12.6). Очевидно, что проверочные элементы, сформированные из принятых информационных, при отсутствии ошибок должны совпадать с принятыми проверочными. 3. Переданная кодовая комбинация имеет вид 1000111 (первая строка матрицы (2.3)). В результате действия помех на приемном конце имеем
В то же время Комбинация b3b2b1 называется синдромом (проверочным вектором). Равенство нулю всех элементов синдрома указывает на отсутствие ошибок или на то, что кодовая комбинация принята с ошибками, которые превратили ее в другую разрешенную. Последнее событие имеет существенно меньшую вероятность, чем первое. Вид ненулевого синдрома определяется характером ошибок в кодовой комбинации. В нашем случае вид синдрома зависит от местоположения одиночной ошибки. В таблице 6.2 отражено соответствие между местоположением одиночной ошибки для кода, заданного матрицей (6.3), и видом синдрома.
Таким образом, зная вид синдрома, можно определить место, где произошла ошибка, и исправить принятый элемент на противоположный. 4. Передавалась кодовая комбинация 1000111. Принята кодовая комбинация 0000111. Синдром имеет вид 111. В соответствии с таблицей 6.2 исказился первый элемент (a1). Изменим первый элемент на противоположный:
Полученная в результате исправления ошибки кодовая комбинация совпадает с переданной. Рассмотренный код (6,4) гарантированно обнаруживает двукратные ошибки, а исправляет только однократные ошибки.
Циклические коды. В теории циклических кодов кодовые комбинации обычно представляются в виде полинома. Так, n-элементная кодовая комбинация записывается в виде
Где ai={0,1}, причем ai=0 соответствуют нулевым элементам комбинации, а ai=1 – ненулевым. Например, комбинациям 1101 и 1010 соответствуют многочлены при формировании комбинаций циклического кода часто используют операции сложения многочленов и деления одного многочлена на другой. Так,
Поскольку
деление выполняется, как обычно, только вычитание заменяется суммированием по модулю два. Разрешенные комбинации циклического кода обладают двумя очень важными отличительными признаками: циклический сдвиг разрешенной комбинации тоже приводит к разрешенной кодовой комбинации. Все разрешенные кодовые комбинации делятся без остатка на полином р(х), называемый образующим. Эти свойства используются при построении кодов, кодирующих и декодирующих устройств, а также при обнаружении и исправлении ошибок. Найдем алгоритмы построения циклического кода, удовлетворяющего перечисленным выше условиям. Задан полином Обозначим многочлен, соответствующий комбинации простого кода, q(x). Возьмем произведение q(x)xr и разделим его на р(х). В результате получим многочлен g(х) и остаток r(х)/р(х):
Умножим левую и правую части на p(x), тогда (6.10) перепишется в виде
перепишем равенство (6.11) в виде
левая часть (2.12) делится без остатка на p(x), значит, без остатка делится и правая часть. Из (6.12) вытекают два способа формирования комбинаций циклического кода: путем умножения многочлена g(x) на p(x) и путем деления q(x)xr на p(x) и приписывания к q(x)xr остатка от деления r(x). 5. Задан полином g(x)=x3+x, соответствующий комбинации простого кода. Сформировать комбинацию циклического кода (7,4) с производящим полиномом р(х)=х3+х2+1. Можно получить комбинацию циклического кода в виде g(x)p(x)=(x3+x)(x3+x2+1)=x6+x5+x4+x. Однако в полученной комбинации нельзя отделить информационные элементы от проверочных, и код получается неразделимым. Перейдем ко второму способу, который чаще всего применяется на практике. Проделаем необходимые операции по получению комбинации циклического кода: 1) G(x)xr=(x3+x)x3=x6+x4; 2)
3) (x6+x4+1) – комбинация циклического кода, полученная методом деления на производящий полином. Она может быть переписана в виде 1010001. Первые четыре элемента – информационные, последние три - проверочные, т.е. Полученный код – разделимый.
Для обнаружения ошибок в принятой кодовой комбинации достаточно поделить ее на производящий полином. Если принятая комбинация разрешенная, то остаток от деления будет нулевым. Ненулевой остаток свидетельствует о том, что принятая комбинация содержит ошибки. По виду остатка (синдрома) можно в некоторых случаях также сделать вывод о характере ошибки и исправить ее. Циклические коды достаточно просты в реализации, обладают высокой корректирующей способностью (способностью исправлять и обнаруживать ошибки) и поэтому рекомендованы мсэ-т для применения в аппаратуре пд. Согласно рекомендации v.41 в системах пд с ос рекомендуется применять код с производящим полиномом p(x)=x16+x12+x5+1.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.212.145 (0.027 с.) |
 Рис. 6.1 – Классификация корректирующих кодов
Рис. 6.1 – Классификация корректирующих кодов (6.1)
(6.1) q2a2
q2a2 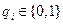 при условии, что хотя бы один из коэффициентов qi≠0. Дополним каждую кодовую комбинацию в (6.1) проверочными элементами так, чтобы обеспечивалось d0=3. Будем иметь в виду также тот факт, что к числу разрешенных комбинаций корректирующего кода принадлежит и комбинация 0000...0, называемая нулевой. Очевидно, что в числе добавляемых проверочных элементов должно быть не менее двух единиц. Тогда общее число единиц в каждой комбинации кода получим не меньше трех и комбинации, полученные нами, будут отличаться от нулевой, по крайней мере, в трех элементах. Добавим по две единицы к каждой строке матрицы (6.1):
при условии, что хотя бы один из коэффициентов qi≠0. Дополним каждую кодовую комбинацию в (6.1) проверочными элементами так, чтобы обеспечивалось d0=3. Будем иметь в виду также тот факт, что к числу разрешенных комбинаций корректирующего кода принадлежит и комбинация 0000...0, называемая нулевой. Очевидно, что в числе добавляемых проверочных элементов должно быть не менее двух единиц. Тогда общее число единиц в каждой комбинации кода получим не меньше трех и комбинации, полученные нами, будут отличаться от нулевой, по крайней мере, в трех элементах. Добавим по две единицы к каждой строке матрицы (6.1): (6.2)
(6.2)
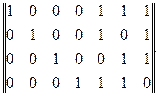 (6.3)
(6.3) (6.4)
(6.4)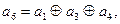 (6.5)
(6.5) (6.6)
(6.6)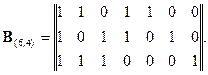

 . Произведем проверки (12.4)-(12.6):
. Произведем проверки (12.4)-(12.6): (6.7)
(6.7) (6.8)
(6.8) (6.9)
(6.9) т.е.
т.е.  что говорит о наличии ошибок в принятой кодовой комбинации. При отсутствии в принятой кодовой комбинации ошибок
что говорит о наличии ошибок в принятой кодовой комбинации. При отсутствии в принятой кодовой комбинации ошибок 


 и
и 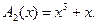

 рассмотрим операцию деления на следующем примере:
рассмотрим операцию деления на следующем примере:
 определяющий корректирующую способность кода, и задан исходный простой код, который требуется преобразовать в корректирующий циклический.
определяющий корректирующую способность кода, и задан исходный простой код, который требуется преобразовать в корректирующий циклический. (6.10)
(6.10) (6.11)
(6.11) (6.12)
(6.12)