
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм Кируса-Бека отсечения отрезка выпуклым многоугольником
Повышение быстродействия алгоритмов отсечения возможно за счет использования более эффективного метода определения местоположения точки отрезка относительно отсекающего окна. Такой метод заложен в алгоритме Кируса-Бека. Он использует для решения этой задачи вектор нормали к ребрам многоугольника. При этом выпуклый многоугольник представляется как область пересечений полуплоскостей, ограниченных прямыми, проходящими через ребра многоугольника (рис. 13). Внутренней нормалью к ребру многоугольника называется единичный вектор перпендикулярный к этому ребру и направленный внутрь многоугольника. Обозначим внутреннюю нормаль ребра AiAi+1 через ni (I = 1,2,...,n). Если f - некоторая точка, лежащая на ребре многоугольника, n - внутренняя нормаль к этому ребру, а P - некоторая точка, полуплоскости, то знак скалярного произведения нормали и вектора из точки f в точку P определяет положение точки относительно грани, содержащей данное ребро (рис. 14). V = n * (P - f). Если взять точку f, совпадающую с вершиной многоугольника, то можно рассмотреть следующие три характерных случая расположения точки P, принадлежащей отрезку P1P2 (рис. 15). Первый случай - угол между векторами n и (P-f) больше 900: V = n * (P - f) < 0, Второй случай - угол между векторами n и (P-f) равен 900: V = n * (P - f) = 0, Третий случай - угол между векторами n и (P-f) меньше 900: V = n * (P - f) > 0, Для построения алгоритма здесь используется параметрическая запись прямой, продолжающей отрезок P1P2. P (t) = P1 + (P2 - P1) *t, где t - параметр, определяющий положение точки на прямой. При значениях 0 точка принадлежит отрезку P1P2. Если t < 0, то точка лежит левее точки P1, а при t > 1 - правее P2. В соответствии с этим для точки пересечения прямой с ребром многоугольника (второй случай расположения точки P) можно вычислить параметр t, заменяя точку f на вершину многоугольника Ai: ni *(P1 + (P2 - P1) *t - Ai) = 0. Из этого выражения после преобразований получаем значение параметра. t = Выполним анализ полученного выражения. Для этого рассмотрим случай равенства нулю знаменателя. Это возможно, когда P2 = P1 или же в случае расположения отрезка P1P2 параллельно ребру многоугольника (угол
В случае неравенства нулю знаменателя, значение t дает точку пересечения прямой, продолжающей отрезок, и грани ребра. При значениях t < 0 или t > 1 точка пересечения находится за пределами отрезка P1P2. Тогда при t < 0 данное ребро не влияет на видимость отрезка (рис. 16). При t > 1 отрезок полностью невидим, так как точка пересечения находится правее отрезка (рис. 17). Если ориентацию отрезка поменять на противоположную (поменять местами точки P1 и P2), то рассмотренные последние два случая также поменяются местами. Рассмотрим теперь случай 0 a) ni *(P2 - P1) > 0 b) ni *(P2 - P1) < 0 В первом случае (рис. 18a) видимым является отрезок PP2, во втором (рис. 18b) - отрезок PP1. По этому поводу говорят, что отрезок укорачивается снизу или сверху соответственно. Прямая, продолжающая отрезок P1P2, может пересечь многоугольник только в двух местах. Однако решение уравнения для t относительно всех ребер даст множество решений в интервале 0
|
||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 357; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.228.35 (0.005 с.) |
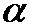 >
>  /2.
/2. t
t 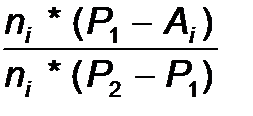 .
.


