
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ЗАДАЧА 1. Решить задачу выпуклого программирования.Стр 1 из 2Следующая ⇒
Реферат В работе решаются семь типовых задач теории оптимизации: 1) Задача выпуклого программирования; 2,3) Задачи линейного программирования 4) Задача классического вариационного исчисления 5) Задача Больца 6) Изопериметрическая задача 7) Задача с подвижными концами 8) Задача Лагранжа В задаче 1 методом множителей Лагранжа находится стационарная точка, далее проверяется выполнение достаточного условия минимума, которое для задач выпуклого программирования сводится к тому, что первый множитель Лагранжа (при целевой функции) должен быть отличен от нуля. В силу свойств выпуклых задач найденная точка локального минимума является одновременно точкой глобального минимума. В задаче 2 графическим методом находится точка минимума функции. Для этого выражаются базисные элементы через свободные, используя метод Гаусса, и затем на графике, учитывая все полученные условия, находится точка минимума. В задаче 3 используется симплекс-метод для нахождения минимума функции. Для этого выражаются базисные элементы через свободные, используя метод Гаусса, и затем составляются симплекс таблицы с последующим их пересчетом по правилам. Из конечной таблицы и находится точка минимума. В задаче классического вариационного исчисления (задаче 4), используется уравнение Эйлера-Лагранжа и начальные условия, находится экстремаль. Далее проверяется выполнение условия глобального минимума. В задаче Больца (задаче 5) используется уравнение Эйлера-Лагранжа, а также условия трансверсальности, находится экстремаль. Далее проверяется выполнение условия глобального минимума. В изопериметрической задаче (задаче 6) применяется метод Лагранжа и, используя уравнение Эйлера-Лагранжа, а также начальное уравнение и краевые условия, находится экстремаль. Далее проверяется выполнение условия глобального минимума. Для решения задачи с подвижными концами (задача 7) применяется метод Лагранжа и, используя уравнение Эйлера-Лагранжа, условия трансверсальности и стационарности, а также краевые условия, находится экстремаль. Далее проверяется выполнение условия глобального минимума. Для решения задачи Лагранжа (задача 8) применяется метод Лагранжа и, используя уравнение Эйлера-Лагранжа, а также условия трансверсальности и начальные условия, находится экстремаль. Далее проверяется выполнение условия глобального минимума.
Оглавление Введение. - 5 - ЗАДАЧА 1. Решить задачу выпуклого программирования. - 8 - ЗАДАЧА 2. Решить задачу линейного программирования графическим методом.. - 10 - ЗАДАЧА 3. Решить задачу № 2 симплекс-методом, используя ЗАДАЧА 4. Решить простейшую задачу классического вариационного исчисления. - 13 - ЗАДАЧА 5. Решить задачу Больца. - 14 - ЗАДАЧА 6. Решить изопериметрическую задачу. - 16 - ЗАДАЧА 7. Решить задачу с подвижными концами. - 18 - ЗАДАЧА 8. Решить задачу Лагранжа. - 20 - Заключение. - 24 - Список использованных источников. - 25 -
Введение
Оптимизация — в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств. Общая запись задач оптимизации задаёт большое разнообразие их классов. От класса задачи зависит подбор метода (эффективность её решения). Классификацию задач определяют: целевая функция и допустимая область (задаётся системой неравенств и равенств или более сложным алгоритмом). Методы оптимизации классифицируют в соответствии с задачами оптимизации: · Локальные методы: сходятся к какому-нибудь локальному экстремуму целевой функции. В случае унимодальной целевой функции, этот экстремум единственен, и будет глобальным максимумом/минимумом. · Глобальные методы: имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции. Существующие в настоящее время методы поиска можно разбить на три большие группы: 1. детерминированные; 2. случайные (стохастические); 3. комбинированные. По критерию размерности допустимого множества, методы оптимизации делят на методы одномерной оптимизации и методы многомерной оптимизации.
Задачи линейного программирования были первыми подробно изученными задачами поиска экстремума функций при наличии ограничений типа неравенств. В 1820 году Фурье и затем в 1947 году Данциг предложил метод направленного перебора смежных вершин в направлении возрастания целевой функции — симплекс-метод, ставший основным при решении задач линейного программирования.
Выделение класса экстремальных задач, определяемых линейным функционалом на множестве, задаваемом линейными ограничениями, следует отнести к 1930-м годам. Одними из первых, исследовавшими в общей форме задачи линейного программирования, были: Джон фон Нейман — математик и физик, доказавший основную теорему о матричных играх и изучивший экономическую модель, носящую его имя, и Канторович — советский академик, лауреат Нобелевской премии (1975), сформулировавший ряд задач линейного программирования и предложивший в 1939 году метод их решения (метод разрешающих множителей), незначительно отличающийся от симплекс-метода. В 1931 году венгерский математик Б. Эгервари рассмотрел математическую постановку и решил задачу линейного программирования, имеющую название «проблема выбора», метод решения получил название «венгерского метода».. Методам линейного программирования посвящено много работ зарубежных учёных. В 1941 году Ф. Л. Хитчкок поставил транспортную задачу. Основной метод решения задач линейного программирования — симплекс-метод — был опубликован в 1949 году Данцигом. Одновременно с развитием линейного программирования большое внимание уделялось задачам нелинейного программирования, в которых либо целевая функция, либо ограничения, либо то и другое нелинейны. В 1951 году была опубликована работа Куна и Таккера, в которой приведены необходимые и достаточные условия оптимальности для решения задач нелинейного программирования. Эта работа послужила основой для последующих исследований в этой области. В настоящее время для эффективного применения методов математического программирования и решения задач на компьютерах разработаны алгебраические языки моделирования, представителями которыми являются AMPL и LINGO.
Основной метод решения задач оптимизации с ограничениями – это метод Лагранжа, метод нахождения условного экстремума функции
Заключение
В курсовой работе получены решения семи типовых задач теории оптимизации: двух конечномерных (задачи выпуклого программирования и линейного программирования) и пяти задач вариационного исчисления (простейшей задачи вариационного исчисления, задачи Больца, изопериметрические задачи, задачи с подвижными концами, и задачи Лагранжа). В результате работы над настоящей курсовой работой были достигнуты следующие цели: — расширен объем и углублены теоретические знания по дисциплине "Методы оптимизации"; — закреплены практические навыки решения задач теории оптимизации; — получены навыки применения метода множителей Лагранжа как основного метода решения задач оптимизации с ограничениями, как конечномерных, так и бесконечномерных; — получен навык подготовки и оформления научно-технической документации.
Реферат В работе решаются семь типовых задач теории оптимизации:
1) Задача выпуклого программирования; 2,3) Задачи линейного программирования 4) Задача классического вариационного исчисления 5) Задача Больца 6) Изопериметрическая задача 7) Задача с подвижными концами 8) Задача Лагранжа В задаче 1 методом множителей Лагранжа находится стационарная точка, далее проверяется выполнение достаточного условия минимума, которое для задач выпуклого программирования сводится к тому, что первый множитель Лагранжа (при целевой функции) должен быть отличен от нуля. В силу свойств выпуклых задач найденная точка локального минимума является одновременно точкой глобального минимума. В задаче 2 графическим методом находится точка минимума функции. Для этого выражаются базисные элементы через свободные, используя метод Гаусса, и затем на графике, учитывая все полученные условия, находится точка минимума. В задаче 3 используется симплекс-метод для нахождения минимума функции. Для этого выражаются базисные элементы через свободные, используя метод Гаусса, и затем составляются симплекс таблицы с последующим их пересчетом по правилам. Из конечной таблицы и находится точка минимума. В задаче классического вариационного исчисления (задаче 4), используется уравнение Эйлера-Лагранжа и начальные условия, находится экстремаль. Далее проверяется выполнение условия глобального минимума. В задаче Больца (задаче 5) используется уравнение Эйлера-Лагранжа, а также условия трансверсальности, находится экстремаль. Далее проверяется выполнение условия глобального минимума. В изопериметрической задаче (задаче 6) применяется метод Лагранжа и, используя уравнение Эйлера-Лагранжа, а также начальное уравнение и краевые условия, находится экстремаль. Далее проверяется выполнение условия глобального минимума. Для решения задачи с подвижными концами (задача 7) применяется метод Лагранжа и, используя уравнение Эйлера-Лагранжа, условия трансверсальности и стационарности, а также краевые условия, находится экстремаль. Далее проверяется выполнение условия глобального минимума. Для решения задачи Лагранжа (задача 8) применяется метод Лагранжа и, используя уравнение Эйлера-Лагранжа, а также условия трансверсальности и начальные условия, находится экстремаль. Далее проверяется выполнение условия глобального минимума.
Оглавление Введение. - 5 -
ЗАДАЧА 1. Решить задачу выпуклого программирования. - 8 - ЗАДАЧА 2. Решить задачу линейного программирования графическим методом.. - 10 - ЗАДАЧА 3. Решить задачу № 2 симплекс-методом, используя ЗАДАЧА 4. Решить простейшую задачу классического вариационного исчисления. - 13 - ЗАДАЧА 5. Решить задачу Больца. - 14 - ЗАДАЧА 6. Решить изопериметрическую задачу. - 16 - ЗАДАЧА 7. Решить задачу с подвижными концами. - 18 - ЗАДАЧА 8. Решить задачу Лагранжа. - 20 - Заключение. - 24 - Список использованных источников. - 25 -
Введение
Оптимизация — в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств. Общая запись задач оптимизации задаёт большое разнообразие их классов. От класса задачи зависит подбор метода (эффективность её решения). Классификацию задач определяют: целевая функция и допустимая область (задаётся системой неравенств и равенств или более сложным алгоритмом). Методы оптимизации классифицируют в соответствии с задачами оптимизации: · Локальные методы: сходятся к какому-нибудь локальному экстремуму целевой функции. В случае унимодальной целевой функции, этот экстремум единственен, и будет глобальным максимумом/минимумом. · Глобальные методы: имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции. Существующие в настоящее время методы поиска можно разбить на три большие группы: 1. детерминированные; 2. случайные (стохастические); 3. комбинированные. По критерию размерности допустимого множества, методы оптимизации делят на методы одномерной оптимизации и методы многомерной оптимизации.
Задачи линейного программирования были первыми подробно изученными задачами поиска экстремума функций при наличии ограничений типа неравенств. В 1820 году Фурье и затем в 1947 году Данциг предложил метод направленного перебора смежных вершин в направлении возрастания целевой функции — симплекс-метод, ставший основным при решении задач линейного программирования. Выделение класса экстремальных задач, определяемых линейным функционалом на множестве, задаваемом линейными ограничениями, следует отнести к 1930-м годам. Одними из первых, исследовавшими в общей форме задачи линейного программирования, были: Джон фон Нейман — математик и физик, доказавший основную теорему о матричных играх и изучивший экономическую модель, носящую его имя, и Канторович — советский академик, лауреат Нобелевской премии (1975), сформулировавший ряд задач линейного программирования и предложивший в 1939 году метод их решения (метод разрешающих множителей), незначительно отличающийся от симплекс-метода. В 1931 году венгерский математик Б. Эгервари рассмотрел математическую постановку и решил задачу линейного программирования, имеющую название «проблема выбора», метод решения получил название «венгерского метода»..
Методам линейного программирования посвящено много работ зарубежных учёных. В 1941 году Ф. Л. Хитчкок поставил транспортную задачу. Основной метод решения задач линейного программирования — симплекс-метод — был опубликован в 1949 году Данцигом. Одновременно с развитием линейного программирования большое внимание уделялось задачам нелинейного программирования, в которых либо целевая функция, либо ограничения, либо то и другое нелинейны. В 1951 году была опубликована работа Куна и Таккера, в которой приведены необходимые и достаточные условия оптимальности для решения задач нелинейного программирования. Эта работа послужила основой для последующих исследований в этой области. В настоящее время для эффективного применения методов математического программирования и решения задач на компьютерах разработаны алгебраические языки моделирования, представителями которыми являются AMPL и LINGO.
Основной метод решения задач оптимизации с ограничениями – это метод Лагранжа, метод нахождения условного экстремума функции
ЗАДАЧА 1. Решить задачу выпуклого программирования.
Составим функцию Лагранжа:
Теперь запишем условия равенства нулю частных производных функции, условие дополняющей нежёсткости и, т.к. ищется минимум функции, условие неотрицательности всех
1) Рассмотрим случай
2) Рассмотрим случай
2.1) Пусть
→ не является точкой минимума, т. к. не выполняются начальные условия 2.2) Пусть
2.3) Пусть
2.4) Пусть
- не может быть точкой минимума.
ЗАДАЧА 2. Решить задачу линейного программирования графическим методом. Во всех вариантах
Будем использовать в качестве базисных переменных x3, x4, x5 и выделять именно их, решая систему методом Гаусса. Запишем систему в матричном виде и решим:
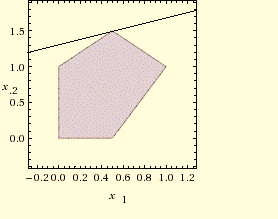
(1-2x+y≥0, 1+x-y≥0,2-x-y≥0, x≥0, y≥0) Построим график системы:
Для получения координат точки минимума исследуемой функции проводим линию уровня нашей целевой функции. Линию уровня для получения минимального значения нужно передвигать влево (т.к. функция прямо пропорциональна x1) и вверх (т.к. функция обратно пропорциональна x2) от градиента до крайней точки многоугольника. Точка минимума находится на пересечении двух прямых, задаваемых уравнениями:
Таким образом, точка M(1/2, 3/2) является точкой минимума данной функции.
ЗАДАЧА 3. Решить задачу № 2 симплекс-методом, используя
Т.к. мы будем искать минимум функции, применим симплекс метод применяется для поиска минимума функции..
Ищем среди коэффициентов pi(коэффициентов целевой функции) pi<0, берем соответствующий этому элементу столбец (кроме столбца свободных членов). Для выбора опорного элемента необходимо найти, какой из них удовлетворит условию минимума отношения свободного члена к данному элементу: После выбора опорного элемента совершаем пересчет таблицы: - опорный элемент заменяем на единицу, деленную на опорный элемент; - опорную строку делим на опорный элемент; - опорный столбец делим на опорный элемент и умножаем на минус единицу; - остальные элементы считаем по «правилу определителя» и делим на опорный элемент - совершаем эти итерации до тех пор, пока в нижней строке все элементы (кроме свободного члена) не станут положительными.
Таким образом мы нашли минимум, ответ сошелся с предыдущей задачей. xmin=(1/2, 3/2, 3/2, 0, 0)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 392; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.125.219 (0.066 с.) |
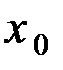 в качестве первоначальной крайней точки. - 11 -
в качестве первоначальной крайней точки. - 11 - , где
, где 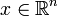 , относительно
, относительно  ограничений
ограничений  , где
, где 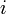 меняется от единицы до
меняется от единицы до 

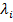 .
.
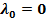 :
: →
→ 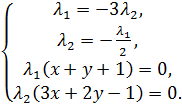
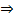 Получаем нулевые
Получаем нулевые  :
:
 :
: →
→  →
→ 

 →
→  →
→  →
→ 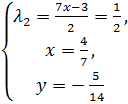 → не является точкой минимума, т. к. не выполняются начальные условия
→ не является точкой минимума, т. к. не выполняются начальные условия :
: →
→  →
→ 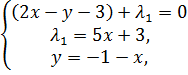 →
→  точка минимума выполняются начальные условия.
точка минимума выполняются начальные условия. :
: →
→ 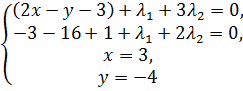 →
→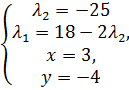 →
→ 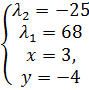
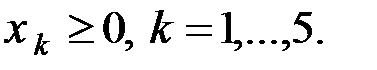

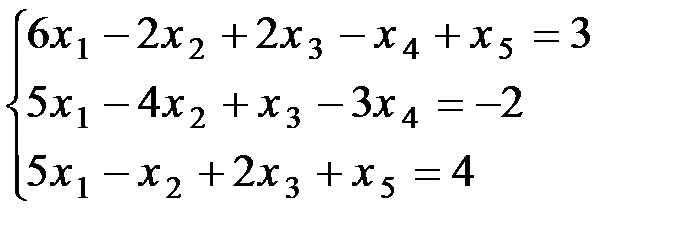
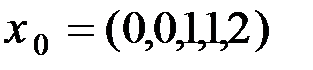

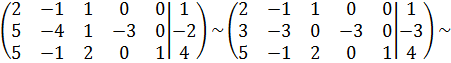





 – наша функция.
– наша функция. , причем
, причем 



