Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корреляционный момент двумерной случайной величины определяется как ⇐ ПредыдущаяСтр 6 из 6
Коэффициент корреляции определяется как
Регрессией Уравнение линейной регрессии
определяет лишь «тенденцию» поведения регрессии Задача 18. Для заданной двумерной случайной величины (X,Y) найти: a) законы распределения компонент и их числовые характеристики; b) выяснить, зависят ли друг от друга компоненты Х и Y. c) условные законы распределения d) регрессию Y на X; e) коэффициент корреляции;
18.1
18.2
18.3
18.4
18.5
18.6
18.7
18.8
18.9
18.10
Пример решения задачи 18. Для заданной двумерной случайной величины Z=(X,Y)
найти: a) законы распределения компонент и их числовые характеристики; b) выяснить, зависят ли друг от друга компоненты Х и Y. c) условные законы распределения d) регрессию Y на X; e) коэффициент корреляции; Решение: a) Найдем законы распределения компонент: Закон распределения компоненты Х получаем суммированием вероятностей по столбцам: Табл.1
Сразу найдем числовые характеристики компоненты Х: Математическое ожидание X: Дисперсия Х: Среднее квадратическое отклонение: Закон распределения компоненты Y получаем суммированием вероятностей двумерной случайной величины Z=(X, Y) по строкам: Табл.2
Убеждаемся, что сумма вероятностей равна единице, как и должно быть для дискретных законов распределения. Найдем числовые характеристики компоненты Y:
Математическое ожидание Y: Дисперсия Y: Среднее квадратическое отклонение: b) Выясним, зависят ли друг от друга компоненты Х и Y. Предположим, что компоненты не зависят друг от друга, тогда вероятность значения двумерной случайной величины
в этом случае закон распределения двумерной случайной величины должен бы иметь вид (используем Табл. 1, и Табл.2)
Закон распределения
Сравнивая полученный закон распределения величины c) Найдем условные законы распределения компоненты Y при фиксированных значениях компоненты X: Табл. 3
Сразу найдем условное математическое ожидание Y при
Табл. 4
Найдем условное математическое ожидание Y при
Табл. 5
Найдем условное математическое ожидание Y при
Тот факт, что таблицы 3, 4, 5 не совпадаю друг с другом еще раз свидетельствуют о зависимости случайных величин друг от друга. d) Найдем регрессию Y на X. Для этого построим график зависимости среднего значения y при фиксированном значении x, т.е. график зависимости условного математического ожидания График регрессии Y на Х
20
-1 0 1 2 x e) Найдем коэффициент корреляции случайных величин Y и X: Коэффициент корреляции
где корреляционный момент может быть найден по формуле
Найдем сначала среднее значение произведения компонент X и Y:
воспользовавшись матрицей вероятностей
откуда для коэффициента корреляции получаем значение
Таким образом, между случайными величинами X и Y имеется достаточно тесная корреляционная связь. Как известно, теснота корреляционной связи определяется тем, насколько коэффициент корреляции отличается по модулю от единицы. Сам же коэффициент корреляции обладает свойством
Чем ближе коэффициент корреляции к единице, тем тесней корреляционная связь компонент X и Y.
Задача 19. Для двумерной случайной величины Z(X, Y) Задачи 18 найти уравнение линейной регрессии Y на Х. График этой регрессии построить в тех же осях и на том же рисунке, что и график самой регрессии Y на Х, построенный в Задаче 18. Сравнить эти графики.
Пример решения задачи 19. Для двумерной случайной величины Z(X, Y) Примера решения задачи 18 найти уравнение линейной регрессии Y на Х. График этой регрессии построить в тех же осях, что и график самой регрессии Y на Х, построенный в Задаче 18. Сравнить эти графики.
Решение: График линейной регрессии Y на X представляет собой тенденцию изменения среднего значения величины Y при фиксированном значении X от этого значения X. Более детальная информацию об этой зависимости при этом теряется. Уравнение линейной регрессии Y на X, которую будем обозначать
и представляет собой канонический вид уравнения прямой на плоскости
При решении Примера18 все эти параметры были найдены: Подставляя их в уравнение линейной регрессии, запишем его в форме
из которой следует, что прямая, проходя через точку A(0,35; 19,5), имеет направляющий вектор График регрессии Y на Х
-1 0 1 2 x То, что регрессия Задача 20. Найти закон распределения случайной величины
Пример решения задачи 20 Найти закон распределения случайной величины Решение: Числовые характеристики компонент X и Y были найдены в примере 18 и записывались в виде:
Математическое ожидание случайной величины V найдем, воспользовавшись свойствами математического ожидания:
Дисперсию случайной величины V также найдем, воспользовавшись свойствами дисперсии
и свойством корреляционного момента
Дисперсия случайной величины V принимает значение:
или в более простой форме:
Для построения закона распределения случайной величины V=5X+Y учтем, что компоненты X, Y являются зависимыми случайными величинами и появления любой пары их значений, дающих в результате значение величины V, может происходить с вероятность
двумерной случайной величины Z=(X,Y)Примера 18:
Закон распределения случайной величины W=5X+Yимеет вид:
Поясним на примере. Так значение Поскольку значения W=25 и W=30 реализуются в испытаниях с вероятностью P=0, т.е. фактически не реализуются (невозможные события). Их можно исключить из закона распределения. Закон распределения случайной величины V=5X+Y, таким образом,имеет вид:
Найдем числовые характеристики случайной величины W, используя их определение и полученный закон распределения. Математическое ожидание V:
Дисперсия W:
Как видим, оба способа вычисления числовых характеристик случайной величины V дают один и тот же результат. Задача 21. Из 20-50 знакомых сверстников (ровесников, соучеников и прочих формальных или неформальных объединений, групп), образующих некоторую выборку, построить вариационный ряд для какого-либо параметра
Пример решения задачи 21. В одной из учебных спортивных групп веса молодых людей в возрасте от 16 до 18 лет задаются таблицей
Считая, что параметр х имеет нормальное распределение, оценить математическое ожидание
Для рассматриваемой выборки найдем выборочную среднюю (математическое ожидание параметра х в заданной выборке)
Выборочная дисперсия
Исправленная дисперсия определяется как
Доверительный интервал для оценки математического ожидания генеральной совокупности
Для значений Доверительный интервал для оценки математического ожидания генеральной совокупности
или, окончательно:
Доверительный интервал для дисперсии
где коэффициент
Доверительный интервал для дисперсии
Оценим вероятность, что наудачу выбранный член сообщества из генеральной совокупности имеет рассматриваемый вес в интервале
a искомая вероятность может быть найдена по формуле
Таким образом, подставляя значения параметров, находим
Из таблицы значений функции Лапласа, (см. Приложение 1), находим значение
Таким образом, имеет место оценка:
которая означает, что наудачу выбранный молодой человек из генеральной совокупности имеет вес от 62 кг до 100 кг с вероятностью 0,38.
ПРИЛОЖЕНИЕ 1. Значения функции Лапласа
Свойство нечетности функции Лапласа:
ПРИЛОЖЕНИЕ 2. Таблица значений Доверительный интервал для оценки математического ожидания
ПРИЛОЖЕНИЕ 3.
Таблица значений Доверительный интервал для оценки среднего квадратического отклонения
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 660; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.244.201 (0.199 с.) |
 .
. .
. на
на  называется функция
называется функция  условное математическое ожидание
условное математическое ожидание  .
.
 ;
; =1
=1
 =4
=4
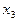 =5
=5
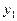 =-1
=-1
 =0
=0
 =2
=2
 =16
=16
 =8
=8





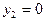



 .
. .
.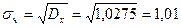 .
.

 .
. .
. .
. должна являться произведение соответствующих вероятностей компонент, т.е.
должна являться произведение соответствующих вероятностей компонент, т.е. ,
,



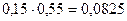

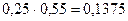



 , убеждаемся в их различии, следовательно, наше предположение о независимости компонент X и Y не верно и компоненты X и Y являются зависимыми случайными величинами.
, убеждаемся в их различии, следовательно, наше предположение о независимости компонент X и Y не верно и компоненты X и Y являются зависимыми случайными величинами.

 взяты из первого столбца заданного закона распределения Z(X, Y), а
взяты из первого столбца заданного закона распределения Z(X, Y), а  сумма по столбцу
сумма по столбцу



 :
: .
.
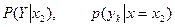
 взяты из второго столбца заданного закона распределения Z(X, Y), а
взяты из второго столбца заданного закона распределения Z(X, Y), а  сумма по столбцу
сумма по столбцу



 :
: .
.

 взяты из второго столбца заданного закона распределения Z(X, Y), а
взяты из второго столбца заданного закона распределения Z(X, Y), а  сумма по столбцу
сумма по столбцу



 :
: .
. от
от  :
:


 30
30 



 определяется как
определяется как ,
, .
.
 заданного закона распределения двумерной случайной величины Z(X, Y)). Тогда коэффициент корреляции будет равен
заданного закона распределения двумерной случайной величины Z(X, Y)). Тогда коэффициент корреляции будет равен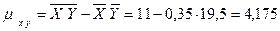 ,
, .
. .
.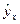 , имеет вид:
, имеет вид: ,
, , здесь
, здесь  математические ожидания компонент X и Y, соответственно;
математические ожидания компонент X и Y, соответственно; их средние квадратические отклонения;
их средние квадратические отклонения; коэффициент корреляции компонент.
коэффициент корреляции компонент.
 ;
;  ;
;  .
. ,
,
 (см. предыдущий Пример) и график линейной регрессии Y на Х
(см. предыдущий Пример) и график линейной регрессии Y на Х  практически совпадают
практически совпадают
 20
20

 A
A

 , которая является по определению прямой, совпадают.
, которая является по определению прямой, совпадают. и ее числовые характеристики, если случайных величин X и Y, являются компонентами двумерной случайной величины Z(X, Y) Задачи 18. Числовые характеристики найти двумя методами: с помощью свойств числовых характеристик и по определению.
и ее числовые характеристики, если случайных величин X и Y, являются компонентами двумерной случайной величины Z(X, Y) Задачи 18. Числовые характеристики найти двумя методами: с помощью свойств числовых характеристик и по определению. и ее числовые характеристики, если случайных величин X и Y, являются компонентами двумерной случайной величины Z(X, Y) Примере 18. Числовые характеристики найти двумя методами: с помощью свойств числовых характеристик и по определению.
и ее числовые характеристики, если случайных величин X и Y, являются компонентами двумерной случайной величины Z(X, Y) Примере 18. Числовые характеристики найти двумя методами: с помощью свойств числовых характеристик и по определению.

 .
. .
.
 постоянные)
постоянные) .
.
 ,
,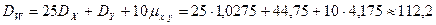 .
. , которая задается матрицей вероятности
, которая задается матрицей вероятности может быть реализовано в испытании, только когда значение X=-1, а значение Y=10, вероятность их совместного появления соответствует вероятности P=0,1.
может быть реализовано в испытании, только когда значение X=-1, а значение Y=10, вероятность их совместного появления соответствует вероятности P=0,1. .
.
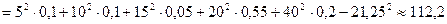 .
. по выборочной средней при помощи доверительного интервала и дисперсию
по выборочной средней при помощи доверительного интервала и дисперсию  этого распределения с надежность 0,95. Оценить вероятность, что наудачу выбранный член сообщества из генеральной совокупности имеет рассматриваемый параметр в интервале
этого распределения с надежность 0,95. Оценить вероятность, что наудачу выбранный член сообщества из генеральной совокупности имеет рассматриваемый параметр в интервале  .
. .
. вычисляется аналогично:
вычисляется аналогично: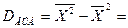
 .
. .
. 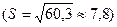 .
. найдем с помощью таблицы коэффициентов
найдем с помощью таблицы коэффициентов 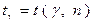 , взятых из приложения 2, по формуле
, взятых из приложения 2, по формуле .
. находим из приложения 2:
находим из приложения 2: 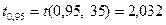 .
. ,
,
 .
.
 ,
,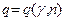 берем из таблицы приложения 3:
берем из таблицы приложения 3:  . Откуда имеет место неравенство.
. Откуда имеет место неравенство. .
. .
.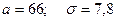 , расположенные по середине доверительных интервалов. Плотность распределения случайной величины будет иметь вид
, расположенные по середине доверительных интервалов. Плотность распределения случайной величины будет иметь вид ,
,

 ,
, ,
, .
.
 ;
; 
 нормального распределения при неизвестном
нормального распределения при неизвестном  :
: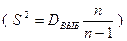

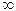

 нормального распределения:
нормального распределения: