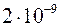Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модифицированные методы Эйлера
Первый модифицированный метод Эйлера. Суть этого метода состоит в следующем. Сначала вычисляются вспомогательные значения искомой функции
Затем находится значение правой части исходного уравнения в средней точке Эти формулы являются расчетными формулами первого модифицированного метода Эйлера. Первый модифицированный метод Эйлера является одношаговым методом со вторым порядком точности. Второй модифицированный метод Эйлера – Коши. Суть этого метода состоит в следующем. Сначала вычисляются вспомогательные значения
Затем приближения искомого решения находятся по формуле:
Эти формулы являются расчетными формулами второго модифицированного метода Эйлера – Коши. Второй модифицированный метод Эйлера – Коши так же, как и первый, является одношаговым методом со вторым порядком точности. Оценка погрешности. Приближенная оценка погрешности модифицированных методов Эйлера осуществляется как и для простого метода Эйлера с использованием правила Рунге. Так как оба модифицированных метода Эйлера имеют второй порядок точности, т. е. Используя правило Рунге, можно построить процедуру приближенного вычисления решения задачи Коши модифицированными методами Эйлера с заданной точностью Приближенным решением будут значения Пример 2. Применим первый модифицированный метод Эйлера для решения задачи Коши
Решение представим в виде таблицы 7. Таблица 7
Третий столбец таблицы 3 содержит приближенное решение
Пример 3. Применим второй модифицированный метод Эйлера – Коши для решения задачи Коши
В соответствии с данными формулами получим расчетную формулу метода Эйлера – Коши:
где Решение представим в виде таблицы 8.
Таблица 8
Таблица 8 заполняется последовательно по строкам, сначала первая строка, затем вторая и т. д. Третий столбец таблицы 8 содержит приближенное решение Сравним полученное приближенное решение с точным решением, представленном в таблице 7. Видим, что погрешность составляет
Метод Рунге – Кутта Метод Рунге – Кутта является одним из наиболее употребительных методов высокой точности. Метод Эйлера можно рассматривать как простейший вариант метода Рунге – Кутта. Рассмотрим задачу Коши для дифференциального уравнения Как и в методе Эйлера, выберем шаг Обозначим через Приведем расчетные формулы метода Рунге – Кутта четвертого порядка точности:
Оценка погрешности. Оценка погрешности метода Рунге – Кутта затруднительна. Грубую оценку погрешности дает правило Рунге. Так как метод Рунге – Кутта имеет четвертый порядок точности, т. е. Используя правило Рунге, можно построить процедуру приближенного вычисления решения задачи Коши методом Рунге – Кутта четвертого порядка точности с заданной точностью Приближенным решением будут значения Пример 4. Методом Рунге-Кутта четвертого порядка точности найдем решение на отрезке
Возьмем шаг Расчетные формулы имеют вид:
Задача имеет точное решение: Найденные приближенные значения решения Таблица 9
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 687; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.173.112 (0.01 с.) |
 в точках
в точках  с помощью формулы:
с помощью формулы: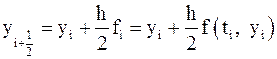 .
. и затем полагается
и затем полагается 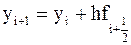 ,
,  .
. .
. .
. , то оценка погрешности примет вид:
, то оценка погрешности примет вид:  .
. . Нужно, начав вычисления с некоторого значения шага
. Нужно, начав вычисления с некоторого значения шага  , последовательно уменьшать это значение в два раза, каждый раз вычисляя приближенное значение
, последовательно уменьшать это значение в два раза, каждый раз вычисляя приближенное значение  . Вычисления прекращаются тогда, когда будет выполнено условие:
. Вычисления прекращаются тогда, когда будет выполнено условие:  .
. .
. , рассмотренной ранее в предыдущем примере. Возьмем шаг
, рассмотренной ранее в предыдущем примере. Возьмем шаг  . Тогда
. Тогда 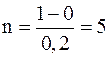 , и расчетная формула первого модифицированного метода Эйлера имеет вид:
, и расчетная формула первого модифицированного метода Эйлера имеет вид:  , где
, где ,
,  ,
,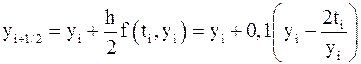 ,
,  .
.
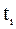

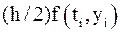


 . Сравнивая полученное приближенное решение с точным решением, представленном в таблице 2, видим, что погрешность составляет
. Сравнивая полученное приближенное решение с точным решением, представленном в таблице 2, видим, что погрешность составляет .
.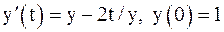 , рассмотренной ранее в примерах 1 и 2. Так же, как и ранее, зададим шаг
, рассмотренной ранее в примерах 1 и 2. Так же, как и ранее, зададим шаг  ,
, ,
, 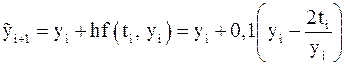 ,
,  ,
,  ,
,  .
.



 .
. .
.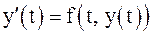 с начальным условием
с начальным условием  .
. и построим сетку с системой узлов
и построим сетку с системой узлов  .
. ,
, 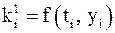 ,
, ,
,  ,
, ,
, 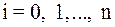 .
. , то оценка погрешности примет вид:
, то оценка погрешности примет вид:  .
. .
. следующей задачи Коши
следующей задачи Коши  .
.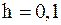 . Тогда
. Тогда  .
. ,
,  ,
,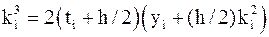 ,
,  ,
,  .
. , поэтому погрешность определяется как абсолютная величина разности между точными и приближенными значениями
, поэтому погрешность определяется как абсолютная величина разности между точными и приближенными значениями  .
. представлены в таблице 9.
представлены в таблице 9.